Based on the investigation of the off-centre field
it is possible to predict
the number of identified stars in a central field at about 
,
where the density is 
times higher than in the off-centre field
(Sect. 1).
The I-band luminosity
function of the off-centre field starts to turn over
at a number density of 
per 
in the PC frame (Fig. 2 (click here)).
In a field with density 40 times higher than this,
the turn-over would correspond to a
magnitude of 
, or at the very brightest end of
the luminosity function where the number density drops to zero.
An interesting question is whether it is possible to find
stars of 
in the central region of M 32.
(This magnitude corresponds to 
,
the expected tip of the red-giant branch
for metal-poor stars, e.g. Lee et al. 1993, and could provide
an estimate of the distance to the galaxy).
To address this question we have investigated a central field in M 32
(archive data, ID 5464),
the analysis being virtually identical to that of the off-centre field.
(The addition of artificial stars was split up so that no more than one
magnitude group at a time, corresponding to 
stars, was added to
the programme frame).
The luminosity function of the central field is seen in Fig. 7 (click here).
Figure 7: Luminosity function for objects
identified in I in the HST PC-frame centered on M 32.
A total of 1606 objects were found in an annulus of area 
and radius 
. The median indicated at the top is 
.
Only a few of the very brightest stars can be considered to be
single objects
Apparently we do see stars of magnitude (Fig. 7 (click here)). However,
when we discuss the central field, we also have to consider the confusion
that spurious detections due to SBF may cause, i.e., the confusion between
single objects and detection of statistical lumps in the background of
unresolved stars
(they both have the shape of the PSF).
This problem is illustrated in Fig. 8 (click here)
where we see that bright objects around, e.g., are indeed
detected and
located in the recovery tests with artificial stars of magnitude 
and
fainter.
The completeness tests show that if stars of
magnitude are present
in the centre of M 32, then we will be able to identify them
(the data in Fig. 8 (click here) imply a limiting magnitude at half probability
of I1/2 = 21.6 for the central field of M 32).
What we do not know is how large a fraction of the
supposedly identified bright stars in Fig. 7 (click here)
are merely compounds of fainter, unresolved stars.
The limiting magnitude itself gives us no information about that.
As will be evident from the following, we can only expect very few of the
brightest stars of the observed luminosity function to be single objects.
Figure 9 (click here) illustrates that it is not possible to distinguish
between the distributions of stars added at and fainter.
That is, when we identify a star with magnitude
or fainter, then we can by no means tell the true
magnitude of that star.
The completeness tests imply a limiting magnitude of
I1/2=21.6 as mentioned above, but this limit only
indicates the detection probability.
We are inclined to disregard the stars in Fig. 7 (click here)
that are fainter than
(i.e., even stars brighter than I1/2),
since we have no reason to believe that they are single point sources.
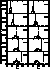
Figure 8: Results of our I-band artificial-star
experiments, now for
the central region of M 32, approximately from the centre.
Again, the number-axis is arbitrary (Sect. 3)
This is further emphasised by a simple simulation of the stellar field at
:
As the stellar content we adopt only one type of stars, namely stars
of magnitude 
(Sodemann & Thomsen 1996).
Our HST-Sim routines add the required number of such "fluctuation stars"
(PSFs) of magnitude 
to reach the average surface brightness of
as observed for the central frame,
and photometry is carried out by DAOPHOT II.
The luminosity function of this simulated stellar field is seen
in Fig. 10 (click here) and should be compared with the
luminosity function of the observed central field (Fig. 7 (click here)).
The similarities are striking and tell us that the objects in
Fig. 7 (click here) may all, except for a very few of the brightest,
be described as mere fluctuations and
not as single point sources.
Based on Fig. 10 (click here) we may explain the observed
"skewness" in Fig. 9 (click here) as follows.
Those of the faint added stars which were located
on top of a bright fluctuation
have inevitably been measured too bright and therefore end up in the left part
of the "magnitude bands" of recovered stars
(a magnitude band being defined by the 93.75 and 6.25 percentiles), whereas
the stars in the right part of the "magnitude bands"
were located on top of a less bright fluctuation.
We do not correct the observed luminosity functions for incompleteness and
binjumping for the following reasons.
Concentrating on the I-band,
for the field at 
the histograms of recovered stars are
distinguishable for magnitudes that correspond to the giant branch and
down to 
where incompleteness starts to set in
(Figs. 1 (click here) and 3 (click here)).
In this paper we do not require the incompleteness-corrected luminosity
function, and correction for binjumping would only affect the
magnitudes around the limiting magnitude.
For the field at , the luminosity function is
comparable to any of the distributions of added test stars fainter than
,
and an attempt to deconvolve the effects of "binjumping"
would thus be an ill-posed problem.
Figure 9: Same data as Fig. 8 (click here)
(besides three extra sets of artificial stars)
but plotted in a slightly different way
(error indicators are as in Figs. 3 (click here) and 4 (click here)).
As emphasized in the text,
must be a unique function of 
,
and we must be certain that we are measuring the added star and not
a statistical lump of unresolved stars, before we can claim that we
are able to carry out reliable photometry.
This is clearly not the case for
magnitudes fainter than . From that magnitude and onwards
it is no longer
possible to distinguish between the distributions of recovered stars.
Therefore, only a few of the very brightest stars
with 
in Fig. 7 (click here)
may be expected to be single objects
Figure 10: Luminosity function of a simulated
stellar field with , as observed for the
central field, but generated from only one type
of stars, namely stars of magnitude
(vertical line), see text.
Note the similarities to
the observed luminosity function (Fig. 7 (click here)).
The median indicated at the top is 
.
(The histogram above has been normalised to the same number of objects as
that of Fig. 7 (click here))