The luminosity functions and CM diagrams of the off-centre field of M 32 are seen in Figs. 1 (click here) and 2 (click here). With the artificial-star experiments as our basis we will now discuss the uncertainty associated with the identified stars.
Figure 1: Luminosity functions for objects identified
in I and V, respectively, in the HST PC-frame at 
from the
centre of M 32. A total of 19461 stars were found to match in I and V.
No correction for M 31 has been made, see text.
The slope of the I-band luminosity function is found to be 0.42. (This
value is not used elsewhere in this paper)
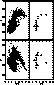
Figure 2: Colour-magnitude diagram of the off-centre
field in M 32. This figure was produced by matching the objects
in Fig. 1 (click here).
The 2
12
star signs show the magnitude and colour of
the stars in our artificial-star experiments
Figure 3: Results of our I-band artificial-star
experiments.
For each magnitude group of added stars (vertical line)
the histogram of recovered stars is
shown. Note, the number-axis is arbitrary (Sect. 3). To clarify the
implications of image crowding we plot several error indicators, in addition
to the mean absolute deviation (MAD), of the magnitude of the recovered star
.
This demonstrates that
the distribution of recovered stars is skewed towards brighter magnitudes,
that is, the faintest objects are found too bright. This "bin jumping" was
discussed by Drukier et al. (1988)
Figure 4: Same as Fig. 3 (click here) but now for the
V-band
In Figs. 3 (click here) and 4 (click here) the magnitude of each group of
added stars is indicated by a vertical line.
The magnitudes of the
recovered stars are binned into histograms of 
bins,
one histogram for each magnitude group of added stars.
Each of the histograms has been normalised
so that they all cover the same number of stars
(implying that the number-axis is arbitrary).
This illustrates that the brightest stars are easily identified,
whereas fainter stars are "spread out" from their original magnitude
(the vertical line) to surrounding magnitudes.
Firstly, note that for the faintest bins the probability of a star being found
in a bin other than the one to which it was added is nonvanishing.
If we want to correct the luminosity function for incompleteness,
this "bin jumping" has to be taken into account (Drukier et al.\
1988). Secondly, the "bin jumping" is clearly asymmetric with an
extended tail of bright measurements.
As the measurement errors are clearly not Gaussian
we shall replace the usual, but now inadequate,
standard deviation 
by the mean absolute deviation (MAD).
(The MAD is
related to the median as the standard deviation is related to the mean,
but the MAD does not require that the distribution of the errors
is Gaussian and it is a more robust estimator than is the mean,
Press et al. 1992).
In addition, we supplement with the lower and upper quartile,
and several percentiles, of the magnitude of the
recovered star .
These numbers are indicated in Figs. 3 (click here) and 4 (click here)
and illustrate that the faintest stars in the CM diagram
are very likely identified too bright by several tens of a magnitude
as compared to their true, unaffected magnitude.
Note, the straight lines
represented by diamond symbols in Figs. 3 (click here), 4 (click here),
and 9 (click here) indicate the magnitude of
the added stars 
and the expected magnitude of the
recovered stars if they are not affected by "binjumping",
i.e., 
.
In order to claim that we are able to carry out reliable photometry,
must be a unique function of ,
and we must be certain that we are measuring the added star and not
a statistical lump of unresolved stars.
The distribution of the colour of recovered stars is, however, fairly symmetric
and much less wide than that of the two passbands individually
(Fig. 5 (click here)).
That is, the added stars which undergo "bin jumping" tend to keep their
original colour, mainly because they are most likely identified on top of a star
with a colour similar to their own - the majority of stars in the CM
diagram are found along the giant branch with 
.
We may therefore expect that the colours of the stars in the CM diagram
are correct.
Figure 5: Colour deviation of recovered stars for
the 9 artificial I-band magnitudes (error indicators are as in
Figs. 3 (click here) and 4 (click here)).
This shows that stars are very likely to be found with the correct colour.
The explanation is that
the majority of stars in the CM diagram (Fig. 2 (click here))
have more or less identical colours
Figure 6 (click here) illustrates that the asymmetric distribution in the
histogram of recovered stars is not a result of plotting the
number of stars as a function of magnitude.
We generated a Gaussian distribution of fluxes according to
,
where N0 = 106, f0 = 1.0, and 
.
The corresponding magnitudes 
were binned into
bins.
The increase in the number of stars fainter than f0 (m > 0)
exceeds a small increase just below m = 0 and is clearly opposite
the asymmetry seen in Figs. 3 (click here) and 4 (click here).
Note that Secker & Harris (1993) adopt a Gaussian function to
represent the measurement error as a function of magnitude.
Figure 6: Asymmetry that arises due to the effect of
plotting a histogram of stars as a function of magnitude
, where the distribution in flux f is Gaussian
(arbitrary number-axis).
The asymmetry is opposite that of the histograms
in Figs. 3 (click here) and 4 (click here)
The limiting magnitudes at half probability are
V1/2 = 26.2 and I1/2 = 25.1 for the M 32 off-centre field.
The limiting magnitudes are based on all the
stars plotted in Figs. 3 (click here) and 4 (click here), respectively,
i.e., regardless of the associated error estimate.
Note, the standard deviation , as calculated by ALLSTAR,
amounts to only 
and 
at the limiting magnitudes
for I and V, respectively,
whereas the MAD is higher by a factor of 3.8 and 2.8 as compared
to the standard deviation (for a Gaussian distribution
).
This merely indicates that in the present investigation
the standard deviation, as given by ALLSTAR,
may be considered too optimistic.