4. Binarity among the sample

4.1. Criterion of variability

To take into account the errors of measurements on the determination of the duplicity, we computed the value for each star of the programme: where n is the number of measurements, E the external error and I the internal error. We then used an F-test which gives the probability that the variations of velocity are only due to the internal dispersion. A star will be considered as double or intrinsically variable if is less than 0.01 (Duquennoy & Mayor 1991). Naturally, this test cannot say anything about the nature of the variability.

The distribution of for non-variable stars should be flat from 0 to 1, while the variable stars should gather at the smallest values of . Therefore, this method allows to appreciate a posteriori the estimate of internal errors. Indeed, if these errors are underestimated, a gradient appears in the distribution of in favour of small values, while if they are overestimated, a peak appears near 1, indicating an abnormally strong predominance of constant stars.

In our case, the internal error is estimated by the quadratic sum of a term which depends on the width of the H line and the quality of the spectrum, and a second term related with the instrumental shift during the night. While the last term is rather well controlled, the first one is not well-known. Indeed, it strongly depends on the choice of the limits (see Sect. 3.2). The internal error can be written:

where is the dispersion due to , and S/N, is the dispersion due to instrumental drift and is adjusted to obtain a flat distribution of on the interval [0,1], except for the small values of course. indicates the quality of the preliminary estimation of I. To determine quantitatively, one uses the cumulative distribution of which must approximate a straight line in the case of a flat distribution. For a given , one can compute the residuals to the regression line fitting the cumulative distribution. The parameter corresponding to the minimum residuals is then adopted. Figure 5 (click here) shows the behaviour of the rms deviation of the residuals as a function of . A minimum clearly appears around . This means that the error on is underestimated by about 20%, which is quite reasonable considering the numerous uncertainties affecting its determination. Figure 6 (click here) shows the histogram and cumulative distribution of for , as well as the straight line minimising the residuals of the cumulative distribution.

  
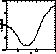
Figure 5: Standard deviation of the residuals as a function of the parameter

  
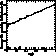
Figure 6: Histogram and cumulative distribution of the for the 50 A and F giant stars. These distributions correspond to an parameter of 1.2 ensuring a flat distribution between 0 and 1. We have also drawn the straight line determined by a least-squares fit of the cumulative distribution

According to this criterion, 52% of the stars are variable and are listed in Table 4 (click here); the others are listed in Table 5 (click here). Each table gives the spectral type, , the blanketing parameter , and eventually some remarks. The source of the projected rotational velocities is Abt & Morrell (1995) or the Bright Star Catalogue (BSC), except for HD 6706, HD 122703, HD 150453, HD 190172 and HD 217131 whose is determined by the optimum fit of a synthetic spectrum to our observed spectra. The spectral types are taken from Hauck (1986) who refers to Cowley et al. (1969), Cowley (1976), the Michigan catalogue (Houk & Cowley 1975; Houk 1978, 1982), Jaschek (1978) and the BSC. are taken from the Geneva photometry database. The values can differ from those of Hauck (1986) because new measurements have been made and a new reference sequence for the Hyades has been defined (see Sect. 5.1). The value can be weaker by a few thousandths of magnitude in the most unfavourable cases for visual doubles. This effect can only diminish the sample of metallic F giants, while the sample of metallic giants cannot be polluted by non-metallic stars. Remarks D and SB come from the BSC.

 

HD Spectral type Remarks

4338 F2III 0.000 0.009 98 D

24832 F1V 0.000 0.004 150

30020 F4IIIp 0.000 0.089 60 SB

34045 F2III 0.001 0.021 67

60489 A7III 0.000 0.008 15

62437 F0III 0.000 0.008 35

69997 F2III 0.000 0.042 25

82043 F0III 0.000 0.003 51

100418 F9III 0.000 -0.020 33

103313 F0V 0.000 0.009 61

104827 F0IV-V 0.000 0.002 38 SB,D

118295 A7-F0V 0.000 -0.003 135

122703 F5III 0.000 0.008 69

150453 F4III-IV 0.001 -0.033 10

155646 F6III 0.000 -0.034

159561 A5III 0.000 -0.019 210 SB

171856 A8IIIn 0.000 -0.001 110 D

174866 A7Vn 0.001 -0.012 150

176971 A4V 0.000 -0.016 125

177392 F2III 0.000 0.030 120

186005 F1III 0.003 0.006 140 SB

187764 F0III 0.000 -0.003 85

190172 F4III 0.000 -0.001 25

203842 F5III 0.000 -0.006 84

209166 F4III 0.001 0.007 <20 D

216701 A7III 0.000 -0.005 80

 

 

HD Spectral type Remarks

1671 F5III 0.929 0.002 41

2628 A7III 0.510 -0.004 18

6706 F5III 0.746 -0.003 50

10845 A9III 0.770 0.015 85

11522 F0III 0.581 -0.009 120

12573 A5III 0.275 -0.017 95

17584 F2III 0.656 0.015 149

17918 F5III 0.461 0.033 120

21770 F4III 0.808 -0.023 29

48737 F5III 0.065 0.008 70

50019 A3III 0.275 -0.006 120 SB

84607 F4III 0.388 0.023 98 SB

86611 F0V 0.415 -0.015 215 SB

89025 F0III 0.242 0.038 81 SB

92787 F5III 0.719 -0.023 65 SB

108382 A4V 0.881 0.006 65

150557 F2III-IV 0.031 -0.009 67

178187 A4III 0.032 -0.003 35

204577 F3III 0.036 0.008

205852 F3III 0.775 0.020 155

210516 A3III 0.407 -0.017 40

217131 F3III 0.166 -0.016 66

219891 A5Vn 0.186 -0.007 175

224995 A6V 0.543 -0.009 90

 

The stars HD 2628 (3 measurements), HD 10845 (2), HD 11522 (2), HD 24832 (3), HD 62437 (4), HD 69997 (4), HD 1772392 (10) and HD 187764 (7) belong to the catalogue of Scuti stars of Rodriguez et al. (1994). In principle, all of these stars should be detected as variable, but the first three are not. For these, we have only a few measurements separated by several days. As ill luck would have it, for HD 2628 and HD 11522 the exposures are made at the same pulsational phase. For HD 10845, our measurements cover different phases, but the small amplitude of the lightcurve (0.02 mag in the V filter) is probably responsible for the non-detection. For the five Scuti stars detected, we find an average ratio of 110 kms^-1mag^-1 between the peak-to-peak radial velocity and photometric variations, which is compatible with the value of 92 kms^-1mag^-1 given by Breger (1979). Therefore, it seems that the variation of these five objects is only due to pulsation and not to any orbital motion.

Among the stars not detected as variable, five are listed as SB in the BSC: HD 50019, HD 84607, HD 86611, HD 89025 and HD 92787. Low spectroscopic dispersion () and fast rotational velocity may probably explain the large variations reported in the past. Figure 7 (click here) shows for these five stars the rms scatter of the radial velocities in the literature as a function of . For HD 89025, we did not take into account the measurements made by Henroteau (1923), because they differ systematically from the others and would generate an artificially larger dispersion. For the older measurements, there is a clear correlation between dispersion and rotation: when increases from 70 to 215 kms^-1, increases from 7 to 25 kms^-1. Our mean radial velocities values are compatible with the older ones, except for HD 86611 which rotates very fast.

  
Figure 7: Rms scatter of the as a function of for stars considered as SB in the BSC but not detected variable in this paper

In Fig. 8 (click here), we show the behaviour of the external scatter E (which is equivalent to the dispersion of the measurements) as a function of for the fifty giant stars and the seven standards of the programme. Black and open symbols represent respectively non variable and variable stars on the basis of the . A linear regression including only non-variable stars is also represented. This straight line is, as a first approximation, the mean internal error I as a function of and agrees well with the values determined previously. Most of the variable stars clearly appear above this line and then we could also use it as criterion of variability.

  
Figure 8: External scatter E as a function of . Stars with are represeted by black symbols and with by open symbols. Scuti type stars are represented by triangles. A linear regression is shown for constant stars

-Scuti type stars are represented by triangles, the most variable of them having an external scatter of about , which is reasonable for stars with an amplitude of 0.05 mag. We can see that most of the variable stars have an external scatter below and so the origin of this variability remains ambiguous. Some of them are intrinsic variables not as yet classified Scuti. Only stars with can be considered as binaries with a high probability.

4.2. Rate of detection

We have made a simulation to determine the rate of detected variable stars as a function of the period. For this, a sample of 1000 double stars with given periods was created as a first step. A flat distribution of the mass ratio was assumed (Mazeh et al. 1992) with primary components of A and F types (). The orbital elements T ₀, and i are randomly distributed, while the eccentricity is distributed according to Duquennoy & Mayor (1991): when the period is less than 10 days, the orbit is assumed to be circular; for periods between 10 and 1000 days, the eccentricity is distributed following a gaussian with a mean equal to 0.3 and (cases with negative eccentricity were dropped and replaced); for longer periods, the distribution f(e)=2e is assumed. In a second step, the radial velocities of the created sample are computed at the epochs of observation of the real programme stars. Then a random internal error is added to these 50000 radial velocities. Finally the value of each star is computed and we can take the census of detected binary stars for a given period. The results are presented in Fig. 9 (click here) for periods between 1 and 10⁵ days.

  
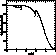
Figure 9: Detection rate as a function of the period. P is given in days

The simulated detection rate is very high for systems with periods below 100 days: it varies between 93.5% and 99.9%. Above 100 days, the rate decreases rapidly, being about 80% for 1000 days and 30% for 10000 days. The discontinuity which appears for 1000 days is due to the strong change in the distribution of eccentricities: indeed, from this point on we grant more importance to large e. The size of this effect is related to the time distribution of the measurements. For instance, if the exposures were more distant in time, the discontinuity would be smaller. The simulation shows some very peaked depressions at shorter periods: at P=30 days, which corresponds to the time interval between two successive observing runs and at dividers of 30, i.e. 15, 10, 7.5, 6 and 5 days. This is completely normal, because for such periods, the time distribution of the measurements makes the detection of binary stars less efficient. At P=3 days and P=2 days, the rate remains very high, because each run lasts for about 4 or 5 days. At P=10 days, there is a weak discontinuity due to the change of distribution of eccentricity, but this effect is hidden inside the peak.

In addition, we have computed the mean rate of detection among binaries with periods less than 100 days. The binaries are created as before but the periods are distributed as a gaussian with a mean equal to and (Duquennoy & Mayor 1991), where P is given in days. When cut-offs at 1 and 100 days were imposed, the detection rate reached 99%, i.e. all close binaries are detected. The rate remains as high as 94% for periods between 1 and 1000 days.