Some stars of the sample rotate very fast and some are very hot, with
effective temperature of about 8000 K. Therefore, these stars cannot be
measured with an instrument such as Coravel, which needs many narrow lines.
The adopted technique consists in fitting a lorentz profile on the
![]() line [4861.331 Å] minimising the
line [4861.331 Å] minimising the ![]() , i.e. the differences
between the lorentz profile and the observed line. The advantage of a
lorentz function over a gaussian is to be more peaked at the centre, so
hydrogen lines are better fitted.
, i.e. the differences
between the lorentz profile and the observed line. The advantage of a
lorentz function over a gaussian is to be more peaked at the centre, so
hydrogen lines are better fitted.
A lorentz profile is defined by 3 parameters (Eq. 1): ![]() is
the centre, i0 the intensity or height and b the half-intensity width
of the profile.
is
the centre, i0 the intensity or height and b the half-intensity width
of the profile.
![]()
The three parameters of ![]() are fitted by least-squares; meanwhile
the optimum choice will depend on the limits fixing the spectral range on
which the fit is made. To avoid too subjective a choice, we fix on both
sides of the line two points determining a segment on which the limit is
randomly chosen (Fig. 1 (click here)). Thus, we generate 100 lorentz profiles
with different limits on each
are fitted by least-squares; meanwhile
the optimum choice will depend on the limits fixing the spectral range on
which the fit is made. To avoid too subjective a choice, we fix on both
sides of the line two points determining a segment on which the limit is
randomly chosen (Fig. 1 (click here)). Thus, we generate 100 lorentz profiles
with different limits on each ![]() line. A profile is taken into
account only if the
line. A profile is taken into
account only if the ![]() value does not exceed 0.05 in order to avoid
hazardous fits. Then, we define for each line
value does not exceed 0.05 in order to avoid
hazardous fits. Then, we define for each line ![]() the mean value of
the central wavelength and the dispersion:
the mean value of
the central wavelength and the dispersion:
![]()
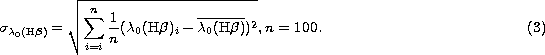
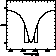
Figure 1: The limits fixing the spectral range on which the fit is made are
randomly chosen on two segments symmetrically placed with respect to the
centre of the line
The dispersion ![]() depends on the physical
properties of the star, essentially the temperature, the surface gravity and
the rotation but also the quality of the spectrum, i.e. the signal-to-noise.
We have chosen to distribute the
depends on the physical
properties of the star, essentially the temperature, the surface gravity and
the rotation but also the quality of the spectrum, i.e. the signal-to-noise.
We have chosen to distribute the ![]() measurements into categories of
decreasing discrete precision on the basis of
measurements into categories of
decreasing discrete precision on the basis of
![]() values (see Table 1 (click here)): measurements
with
values (see Table 1 (click here)): measurements
with ![]() between 0 and 3 mÅ will be
considered as having
between 0 and 3 mÅ will be
considered as having ![]() , those
with
, those
with ![]() between 3 and 6 mÅ will have
between 3 and 6 mÅ will have
![]() , etc. The value of 3 mÅ\
is completely arbitrary, corresponding to a radial velocity of about 0.2
kms-1. The
, etc. The value of 3 mÅ\
is completely arbitrary, corresponding to a radial velocity of about 0.2
kms-1. The ![]() and the central
wavelength
and the central
wavelength ![]() also depend on the choice of
the limits for the fit. This effect is discussed in detail in Appendix A.
also depend on the choice of
the limits for the fit. This effect is discussed in detail in Appendix A.
|
| |
| [0.000, 0.003] | 0.19 |
| [0.003, 0.006] | 0.38 |
| [0.006, 0.009] | 0.56 |
| [0.009, 0.012] | 0.74 |
| ... |
The term ![]() is defined as the internal error due to
the effective temperature, the surface gravity, the rotation and the S/N
ratio. The total internal error includes an additional term due to the
instrumental drift during the night. This variability was similar for the
four missions and Figs. 2 (click here) and 3 (click here) show the fluctuations of
the position of the thorium lines during the night of 6 and 7 November and
during the night of 5 and 6 December 1994 for 3 lines. When we filled up the
nitrogen tank, at the beginning and in the middle of the night, a strong
variation appeared as shown on these figures. Between these jumps, we
observe a regular variation of about 0.12 pixels per hour. We therefore have
a variation of 0.16 kms-1 per 12 minutes which corresponds to the
average time of stellar exposure. For this reason, the internal error due to
this factor (
is defined as the internal error due to
the effective temperature, the surface gravity, the rotation and the S/N
ratio. The total internal error includes an additional term due to the
instrumental drift during the night. This variability was similar for the
four missions and Figs. 2 (click here) and 3 (click here) show the fluctuations of
the position of the thorium lines during the night of 6 and 7 November and
during the night of 5 and 6 December 1994 for 3 lines. When we filled up the
nitrogen tank, at the beginning and in the middle of the night, a strong
variation appeared as shown on these figures. Between these jumps, we
observe a regular variation of about 0.12 pixels per hour. We therefore have
a variation of 0.16 kms-1 per 12 minutes which corresponds to the
average time of stellar exposure. For this reason, the internal error due to
this factor (![]() ) is estimated at 0.16 kms-1.
Finally, the total internal error is written by
) is estimated at 0.16 kms-1.
Finally, the total internal error is written by
![]() .
.
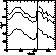
Figure 2: Variation of the position of three lines of thorium during 6 and
7 November 1994. The vertical shift is arbitrary. The vertical line
corresponds to the filling of nitrogen
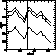
Figure 3: Same as Fig. 2 (click here), but for the night of 5 and 6
December 1994
For standard stars, we prefer to use Coravel values in the system of faint
IAU standard stars (Mayor & Maurice 1985) than IAU values
listed in the Astronomical Almanach because the latter are taken from
various authors and sometimes not updated. For example, the IAU radial
velocity for HD 114762 has been listed as ![]() in
the Astronomical Almanach since at least 1981, while combined data from the
Cfa and Coravel give a systemic velocity of
in
the Astronomical Almanach since at least 1981, while combined data from the
Cfa and Coravel give a systemic velocity of ![]() (Latham et al. 1989).
(Latham et al. 1989).
For the four observing runs, Fig. 4 (click here) shows the difference between radial velocities measured with Aurélie and the Coravel value for each standard star. Our values are higher than the Coravel ones by about 2.75 kms-1. The error bars are defined by the quadratic sum of the internal error (see Sect. 3.1) and the dispersion on the Coravel values. The internal precision of our measurements is very impressive: we obtain a scatter of about 0.4 kms-1 around the mean radial velocity.

Figure 4: Difference between Aurélie radial velocities and Coravel
velocities for the runs of May, June, November and December 1994. HD 693:
open squares. HD 22484: open triangles. HD 89449: crosses. HD 114762: full
circles. HD 136202: full triangles. HD 222368: open circles
Notice that ![]() is clearly smaller for HD 114762 by about 1.4
kms-1. Such a difference can partly be due to the nature of this star,
which has a very small amplitude (Latham et al. 1989 and
Cochran et al. 1991) and to the fact that our measurements were
made precisely when the radial velocity was minimum: in this way we can
explain a shift of about 0.6 kms-1 with respect to the other
standard stars. Unfortunately, we do not find any explanation for the
remaining shift of 0.8 kms-1. The reduction of the spectra was made
again with MIDAS software, only to find the same shift. So, we cannot
question the reduction.
is clearly smaller for HD 114762 by about 1.4
kms-1. Such a difference can partly be due to the nature of this star,
which has a very small amplitude (Latham et al. 1989 and
Cochran et al. 1991) and to the fact that our measurements were
made precisely when the radial velocity was minimum: in this way we can
explain a shift of about 0.6 kms-1 with respect to the other
standard stars. Unfortunately, we do not find any explanation for the
remaining shift of 0.8 kms-1. The reduction of the spectra was made
again with MIDAS software, only to find the same shift. So, we cannot
question the reduction.
We have simply subtracted the mean ![]() from the measured
velocities. The average
from the measured
velocities. The average ![]() are 2.80, 2.49, 2.69 and 2.90
kms-1 for the runs of May, June, November and December respectively.
For the first run, the values of HD 114762 are not taken into account in the
average value. Table 2 (click here) gives the individual corrected radial
velocities and the mean velocity for standard stars; Table 3 lists
the individual corrected radial velocities for the 50 giant A and F stars.
are 2.80, 2.49, 2.69 and 2.90
kms-1 for the runs of May, June, November and December respectively.
For the first run, the values of HD 114762 are not taken into account in the
average value. Table 2 (click here) gives the individual corrected radial
velocities and the mean velocity for standard stars; Table 3 lists
the individual corrected radial velocities for the 50 giant A and F stars.
| HD | HJD | | I |
| (+2449000) | kms-1 | kms-1 | |
| 693 | 663.367 | 15.12 | 0.28 |
| 693 | 692.408 | 15.99 | 0.48 |
| 693 | 693.411 | 15.57 | 0.28 |
| | 15.44 | ||
| 22484 | 663.507 | 27.59 | 0.28 |
| 22484 | 663.528 | 27.97 | 0.48 |
| 22484 | 665.610 | 28.11 | 0.28 |
| 22484 | 689.403 | 27.45 | 0.28 |
| 22484 | 689.450 | 28.05 | 0.48 |
| 22484 | 692.473 | 27.73 | 0.28 |
| 22484 | 692.544 | 27.07 | 0.48 |
| 22484 | 693.546 | 28.62 | 0.28 |
| | 27.86 | ||
| 89449 | 470.375 | 6.07 | 0.28 |
| 89449 | 471.311 | 6.13 | 0.28 |
| 89449 | 472.383 | 5.04 | 0.48 |
| 89449 | 472.433 | 6.87 | 0.69 |
| 89449 | 473.347 | 5.39 | 0.28 |
| 89449 | 474.319 | 6.19 | 0.28 |
| 89449 | 505.366 | 6.49 | 0.28 |
| 89449 | 506.346 | 5.83 | 0.28 |
| 89449 | 507.345 | 4.69 | 0.28 |
| 89449 | 509.356 | 6.03 | 0.28 |
| 89449 | 663.674 | 5.62 | 0.48 |
| 89449 | 692.618 | 5.88 | 0.28 |
| 89449 | 692.681 | 5.65 | 0.28 |
| 89449 | 693.668 | 5.72 | 0.48 |
| 89449 | 693.722 | 6.13 | 0.28 |
| | 5.84 | ||
| 114762 | 470.503 | 47.51 | 0.48 |
| 114762 | 471.411 | 47.38 | 0.28 |
| 114762 | 472.526 | 47.75 | 0.48 |
| 114762 | 473.420 | 48.02 | 0.28 |
| 114762 | 474.432 | 48.01 | 0.28 |
| | 47.77 | ||
| 136202 | 470.593 | 54.33 | 0.48 |
| 136202 | 471.499 | 54.22 | 0.48 |
| 136202 | 472.597 | 54.16 | 0.48 |
| 136202 | 473.555 | 54.30 | 0.48 |
| 136202 | 474.504 | 54.37 | 0.28 |
| 136202 | 505.503 | 54.89 | 0.48 |
| 136202 | 506.474 | 54.93 | 1.56 |
| 136202 | 508.381 | 54.48 | 0.48 |
| | 54.39 | ||
| 187691 | 470.642 | -0.58 | 0.28 |
| 187691 | 471.638 | -0.07 | 0.28 |
| 187691 | 472.638 | 0.21 | 0.28 |
| 187691 | 473.640 | -0.01 | 0.48 |
| 187691 | 474.639 | -0.86 | 0.28 |
| 187691 | 505.598 | 0.23 | 0.28 |
| 187691 | 506.558 | -0.08 | 0.48 |
| 187691 | 507.599 | -0.39 | 0.28 |
| 187691 | 509.501 | -1.30 | 0.48 |
| | -0.27 | ||
| 222368 | 663.287 | 4.76 | 0.28 |
| 222368 | 663.395 | 5.67 | 0.28 |
| 222368 | 689.321 | 4.98 | 0.48 |
| 222368 | 690.296 | 4.39 | 0.28 |
| 222368 | 692.320 | 5.23 | 0.28 |
| 222368 | 693.300 | 5.62 | 0.28 |
| | 5.12 |
|
HD | HJD | | I |
| (+2449000) | kms-1 | kms-1 | |
| 1671 | 663.445 | 10.53 | 0.48 |
| 1671 | 689.354 | 10.55 | 0.28 |
| 1671 | 693.444 | 10.34 | 0.48 |
| 2628 | 663.451 | -10.86 | 0.28 |
| 2628 | 689.366 | -10.67 | 1.12 |
| 2628 | 693.448 | -10.40 | 0.28 |
| 4338 | 663.410 | 2.08 | 0.69 |
| 4338 | 689.381 | -0.47 | 1.34 |
| 4338 | 693.470 | 5.84 | 0.94 |
| 6706 | 663.426 | 23.81 | 0.28 |
| 6706 | 692.487 | 23.57 | 0.69 |
| 10845 | 663.458 | -13.97 | 0.48 |
| 10845 | 689.412 | -13.67 | 0.90 |
| 11522 | 663.436 | 1.16 | 0.69 |
| 11522 | 693.514 | 1.99 | 1.34 |
| 12573 | 663.471 | 8.62 | 0.69 |
| 12573 | 692.522 | 7.38 | 0.90 |
| 17584 | 689.423 | 18.41 | 0.94 |
| 17584 | 663.481 | 18.60 | 0.90 |
| 17584 | 692.387 | 19.42 | 0.69 |
| 17918 | 663.491 | 17.21 | 0.48 |
| 17918 | 663.552 | 18.40 | 0.69 |
| 17918 | 689.434 | 17.11 | 0.90 |
| 17918 | 692.396 | 18.08 | 0.90 |
| 21770 | 663.500 | -46.18 | 0.28 |
| 21770 | 689.444 | -46.35 | 0.48 |
| 21770 | 692.469 | -46.01 | 0.28 |
| 24832 | 663.538 | 20.61 | 1.56 |
| 24832 | 692.433 | 18.20 | 0.90 |
| 24832 | 693.569 | 22.67 | 0.69 |
| 30020 | 663.570 | 34.31 | 0.69 |
| 30020 | 692.567 | 37.19 | 0.48 |
| 30020 | 693.609 | 37.87 | 0.90 |
| 34045 | 663.591 | 29.89 | 0.48 |
| 34045 | 689.467 | 26.19 | 0.94 |
| 34045 | 692.587 | 29.18 | 0.48 |
| 48737 | 663.606 | 26.12 | 0.90 |
| 48737 | 665.620 | 26.30 | 0.48 |
| 48737 | 689.459 | 25.77 | 0.48 |
| 48737 | 692.598 | 27.35 | 0.69 |
| 48737 | 693.630 | 27.56 | 0.48 |
| 50019 | 663.611 | 31.17 | 0.69 |
| 50019 | 664.643 | 30.75 | 0.69 |
| 50019 | 665.626 | 30.30 | 0.69 |
| 50019 | 692.601 | 30.04 | 0.69 |
| 50019 | 693.633 | 32.39 | 0.90 |
| 60489 | 663.617 | 52.67 | 0.69 |
| 60489 | 665.645 | 53.42 | 0.69 |
| 60489 | 692.608 | 30.81 | 0.48 |
| 60489 | 693.650 | 31.65 | 0.28 |
| 62437 | 663.627 | 11.13 | 0.48 |
| 62437 | 665.677 | 14.46 | 1.34 |
|
HD | HJD | | I |
| (+2449000) | kms-1 | kms-1 | |
| 62437 | 692.628 | 15.99 | 0.28 |
| 62437 | 693.639 | 14.12 | 0.69 |
| 69997 | 663.642 | 31.67 | 0.28 |
| 69997 | 692.641 | 32.79 | 0.28 |
| 69997 | 692.703 | 33.18 | 0.28 |
| 69997 | 693.661 | 32.59 | 0.28 |
| 82043 | 663.652 | 12.25 | 0.48 |
| 82043 | 692.649 | 1.73 | 0.69 |
| 82043 | 692.712 | 1.41 | 0.69 |
| 82043 | 693.679 | 0.14 | 0.48 |
| 84607 | 663.660 | 13.65 | 0.48 |
| 84607 | 692.660 | 12.25 | 0.69 |
| 84607 | 692.723 | 13.50 | 0.69 |
| 84607 | 693.690 | 13.09 | 0.48 |
| 86611 | 663.688 | 26.47 | 0.90 |
| 86611 | 692.669 | 24.42 | 0.90 |
| 86611 | 692.732 | 25.79 | 0.69 |
| 86611 | 693.699 | 25.04 | 1.34 |
| 89025 | 692.676 | -21.20 | 0.69 |
| 89025 | 693.710 | -22.07 | 0.28 |
| 92787 | 692.689 | 4.47 | 0.90 |
| 92787 | 692.692 | 4.47 | 0.90 |
| 92787 | 693.715 | 3.82 | 0.48 |
| 100418 | 470.406 | 1.02 | 0.69 |
| 100418 | 471.327 | 0.76 | 0.58 |
| 100418 | 471.390 | -0.57 | 0.69 |
| 100418 | 472.398 | 2.28 | 0.28 |
| 100418 | 473.336 | 0.22 | 0.69 |
| 100418 | 474.359 | -1.81 | 0.48 |
| 100418 | 506.372 | -0.28 | 0.28 |
| 103313 | 470.461 | 16.10 | 0.69 |
| 103313 | 471.340 | 16.75 | 0.48 |
| 103313 | 471.463 | 14.71 | 0.28 |
| 103313 | 472.413 | 19.14 | 0.90 |
| 103313 | 473.359 | 17.59 | 0.69 |
| 103313 | 473.440 | 17.88 | 0.90 |
| 103313 | 474.378 | 16.54 | 0.69 |
| 103313 | 474.414 | 16.72 | 0.48 |
| 103313 | 505.387 | 22.17 | 1.56 |
| 103313 | 507.364 | 18.64 | 0.48 |
| 103313 | 507.397 | 15.74 | 2.01 |
| 104827 | 470.475 | 10.21 | 0.48 |
| 104827 | 471.352 | 8.07 | 0.90 |
| 104827 | 471.399 | 7.33 | 0.48 |
| 104827 | 472.443 | 7.70 | 0.48 |
| 104827 | 473.373 | 7.60 | 0.48 |
| 104827 | 473.482 | 8.42 | 0.48 |
| 104827 | 474.332 | 7.37 | 0.69 |
| 104827 | 474.479 | 6.93 | 0.48 |
| 104827 | 506.394 | 8.89 | 0.48 |
| 108382 | 470.486 | -2.33 | 0.48 |
| 108382 | 471.364 | -1.97 | 0.48 |
| 108382 | 471.471 | -1.82 | 0.48 |
| 108382 | 472.457 | -2.86 | 0.69 |
| 108382 | 473.383 | -1.97 | 0.90 |
| 108382 | 473.430 | -2.71 | 0.69 |
| 108382 | 474.345 | -1.55 | 0.90 |
|
HD | HJD | | I |
| (+2449000) | kms-1 | kms-1 | |
| 118295 | 470.535 | -20.00 | 0.69 |
| 118295 | 471.375 | -19.63 | 0.69 |
| 118295 | 471.447 | -17.52 | 1.56 |
| 118295 | 472.470 | -20.59 | 0.69 |
| 118295 | 473.401 | -18.46 | 0.94 |
| 118295 | 474.394 | -17.76 | 0.69 |
| 118295 | 505.410 | -24.23 | 0.94 |
| 118295 | 506.420 | -19.84 | 1.34 |
| 108382 | 474.446 | -1.89 | 0.90 |
| 122703 | 470.522 | -17.63 | 0.69 |
| 122703 | 471.430 | -13.34 | 0.90 |
| 122703 | 471.485 | -21.60 | 0.69 |
| 122703 | 472.509 | -19.21 | 2.01 |
| 122703 | 473.455 | -15.39 | 0.69 |
| 122703 | 474.464 | -17.16 | 0.94 |
| 150453 | 471.521 | 0.82 | 0.69 |
| 150453 | 471.620 | 0.47 | 0.69 |
| 150453 | 472.586 | 0.12 | 0.28 |
| 150453 | 473.541 | 0.64 | 0.48 |
| 150453 | 474.568 | -0.10 | 0.28 |
| 150453 | 506.486 | 1.54 | 0.28 |
| 150557 | 471.510 | -49.75 | 0.48 |
| 150557 | 472.492 | -49.42 | 0.69 |
| 150557 | 473.496 | -48.36 | 0.90 |
| 150557 | 474.494 | -49.64 | 0.69 |
| 150557 | 474.540 | -50.22 | 0.48 |
| 150557 | 505.532 | -48.20 | 0.48 |
| 150557 | 506.412 | -48.49 | 0.94 |
| 150557 | 506.467 | -50.15 | 0.28 |
| 150557 | 509.393 | -49.60 | 0.48 |
| 155646 | 470.552 | 59.76 | 0.48 |
| 155646 | 471.535 | 61.08 | 0.48 |
| 155646 | 472.542 | 62.36 | 0.48 |
| 155646 | 473.518 | 59.78 | 0.28 |
| 155646 | 474.524 | 58.64 | 0.48 |
| 155646 | 505.545 | 60.05 | 0.48 |
| 155646 | 506.445 | 59.95 | 0.28 |
| 155646 | 506.547 | 60.70 | 0.28 |
| 159561 | 470.565 | 10.69 | 0.69 |
| 159561 | 471.543 | 11.10 | 0.48 |
| 159561 | 472.550 | 12.23 | 0.69 |
| 159561 | 472.631 | 10.25 | 0.94 |
| 159561 | 473.527 | 12.03 | 0.90 |
| 159561 | 474.510 | 10.82 | 0.69 |
| 159561 | 505.431 | 11.46 | 0.90 |
| 159561 | 506.457 | 10.65 | 0.48 |
| 159561 | 507.608 | 9.68 | 0.69 |
| 159561 | 509.446 | 8.29 | 0.48 |
| 171856 | 470.639 | -5.56 | 2.01 |
| 171856 | 473.620 | -5.96 | 1.34 |
| 171856 | 506.584 | -21.70 | 0.48 |
| 171856 | 508.544 | -19.14 | 0.69 |
| 174866 | 470.625 | -39.39 | 0.94 |
| 174866 | 472.615 | -38.50 | 0.69 |
| 174866 | 473.606 | -40.45 | 0.48 |
| 174866 | 505.585 | -40.89 | 0.90 |
| 174866 | 506.571 | -43.56 | 1.34 |
| 174866 | 509.521 | -42.08 | 0.69 |
|
HD | HJD | | I |
| (+2449000) | kms-1 | kms-1 | |
| 176971 | 470.575 | -34.62 | 0.90 |
| 176971 | 471.553 | -34.28 | 0.48 |
| 176971 | 472.559 | -31.63 | 0.69 |
| 176971 | 473.560 | -35.13 | 0.48 |
| 176971 | 474.579 | -33.63 | 0.69 |
| 176971 | 474.625 | -34.88 | 1.34 |
| 176971 | 505.461 | -34.60 | 0.94 |
| 176971 | 506.517 | -32.51 | 0.69 |
| 176971 | 509.414 | -29.47 | 1.78 |
| 177392 | 470.608 | 10.13 | 0.48 |
| 177392 | 471.577 | 9.51 | 1.56 |
| 177392 | 472.603 | 12.38 | 0.69 |
| 177392 | 473.580 | 10.12 | 0.90 |
| 177392 | 474.593 | 6.75 | 0.90 |
| 177392 | 505.481 | 11.21 | 0.90 |
| 177392 | 506.502 | 10.31 | 2.01 |
| 177392 | 508.525 | 6.75 | 0.90 |
| 177392 | 509.459 | 8.69 | 0.28 |
| 177392 | 509.539 | 7.37 | 0.90 |
| 178187 | 470.600 | -24.85 | 0.69 |
| 178187 | 471.563 | -24.43 | 0.69 |
| 178187 | 472.568 | -24.82 | 0.48 |
| 178187 | 473.570 | -25.11 | 0.94 |
| 178187 | 474.602 | -24.69 | 0.90 |
| 178187 | 505.440 | -24.69 | 0.69 |
| 178187 | 505.518 | -25.04 | 0.90 |
| 178187 | 506.531 | -25.03 | 0.90 |
| 178187 | 507.585 | -22.70 | 0.48 |
| 178187 | 508.506 | -23.06 | 0.69 |
| 186005 | 472.623 | -40.39 | 1.34 |
| 186005 | 474.634 | -39.98 | 0.90 |
| 186005 | 506.593 | -39.50 | 0.90 |
| 186005 | 509.593 | -42.63 | 0.48 |
| 187764 | 471.598 | -8.02 | 0.69 |
| 187764 | 473.589 | -5.96 | 0.48 |
| 187764 | 474.551 | -8.39 | 0.90 |
| 187764 | 474.612 | -4.71 | 0.90 |
| 187764 | 505.560 | -6.14 | 0.69 |
| 187764 | 506.554 | -3.10 | 0.69 |
| 187764 | 509.477 | -4.64 | 0.69 |
| 190172 | 471.628 | 2.82 | 0.48 |
| 190172 | 473.628 | 6.00 | 0.28 |
| 190172 | 506.602 | 3.11 | 0.48 |
| 203842 | 663.228 | -25.94 | 0.69 |
| 203842 | 665.246 | -27.74 | 0.48 |
| 203842 | 690.313 | -26.43 | 0.69 |
| 203842 | 692.296 | -24.73 | 0.90 |
| 203842 | 693.243 | -23.22 | 0.48 |
| 204577 | 663.245 | -10.45 | 0.48 |
| 204577 | 693.273 | -8.69 | 0.69 |
| 205852 | 663.262 | -31.90 | 0.90 |
| 205852 | 692.307 | -31.83 | 0.69 |
| 205852 | 693.308 | -32.48 | 0.69 |
| 209166 | 663.275 | 5.22 | 0.28 |
| 209166 | 692.314 | 6.36 | 0.28 |
| 209166 | 693.322 | 6.82 | 0.48 |
|
HD | HJD | | I |
| (+2449000) | kms-1 | kms-1 | |
| 210516 | 663.295 | 10.46 | 0.69 |
| 210516 | 692.332 | 11.38 | 0.94 |
| 210516 | 693.339 | 12.16 | 0.94 |
| 216701 | 663.314 | 12.70 | 0.48 |
| 216701 | 692.352 | 15.26 | 0.69 |
| 216701 | 693.355 | 11.36 | 0.48 |
| 217131 | 663.334 | -12.12 | 0.28 |
| 217131 | 693.374 | -11.35 | 0.48 |
| 219891 | 663.352 | -3.04 | 0.90 |
| 219891 | 689.338 | -3.01 | 2.01 |
| 219891 | 693.396 | -0.48 | 0.94 |
| 224995 | 663.383 | 8.13 | 0.48 |
| 224995 | 689.302 | 7.14 | 0.90 |
| 224995 | 693.431 | 7.48 | 0.69 |