distance from the center of the Sun outward
and has an increasing contribution to the total coronal
brightness at longer wavelengths (see Fig. 57 (click here)).
For measurements in the
corona, the elongation 
is often
expressed in units of , i.e. in terms of
the minimum projected distance r of the line of sight from the center of
the Sun. Because the solar radius is
= 1 AU/214.94 (Allen 1985), 1
in
elongation corresponds to 3.75 (and 
to 16.0'),
while more generally for an observer
at the earth
As mentioned in Sect. 2 (click here), coronal brightnesses often are expressed
in terms of the average brightness of the solar disk as
, where 
/sr.
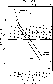
Figure 57: The visible equatorial and polar F-corona brightnesses
in comparison to typical values for K-corona, the aureole (circumsolar
sky brightness enhancement)
and instrumental straylight levels. At 
, the brightnesses
measured in the zodiacal light (see Sect. 8 (click here)) are included
The main uncertainty in
determination of the inner F-corona is the separation from the
K-coronal brightness. A common method
of separation is based on the assumption that the F-coronal
brightness is produced by diffraction of
dust near the observer and
hence unpolarized. This approach may be
suitable for distances, respectively elongations of 
,
the increasing polarization
of the F-corona
at larger elongations
(Blackwell et al. 1967)
however leads to errors of this subtraction
method. A further method of K-coronal separation
uses the depth of Fraunhoferlines in the
Solar spectrum. Both methods are described
in Blackwell et al. (1967).
Ground-based coronal observations generally are made during
solar eclipses, with the local sky brightness constituting the main
disturbance to be corrected for.
The eclipse sky background on the
ground may vary considerably with daily conditions as well as
eclipse site. An early work by
Blackwell et al. (1967) cites values of (
for the eclipse
sky background in the visible light, i.e. at wavelengths from
500 to 830 nm.
For 
, MacQueen & Greeley (1995) report a
value of 10
during the 1991 eclipse sky from Hawaii.
However, these measurements suffered from thin clouds and the
presence of high altitude aerosols from the Pinatubo eruption.
The enhanced circumsolar sky brightness caused by diffraction
on aerosols is called solar
aureole. It may vary with elongation, and may be
described as
a function A(r).
Dürst (1982) derives
values of about 10-11 to 
and a radial
gradient according to
r-1.37 at 600 nm wavelength.
Infrared results differ at
the 1991 eclipse, but
MacQueen & Greeley (1995)
find a description A(r) 
for
the region from 3 to 9 and a constant value of
W cm-2 
m-1
sr-1 (i.e. 
)
beyond for the infrared aureole during the 1991 eclipse.
Instrumental straylight for externally
occulted systems
on satellites presently achieve straylight levels
in the 10-10 to
range and
hence enable coronal observations out to at least
(Brückner
et al. 1995).
The values of polarization in the eclipse sky background range from 7.5% to 30% for ground based observations.
Observations of the F-corona brightness (Fig. 58 (click here)) are made during solar eclipses from ground, from rockets and from balloons in the visible and near infrared regime. Data were taken as well from space borne coronagraphs.
An early review of the visible coronal observations was given by
Blackwell et al. (1967). They gave a description of the
F-corona data as the continuation of the
zodiacal light. A more recent review was given by Koutchmy & Lamy
(1985) including already infrared observations.
They describe the
visible F-corona brightness
at wavelength
400 nm 
600 nm
as proportional to
r-2.25 at the equator and
r-2.47 at the solar poles,
based on a continuation
of the zodiacal light data.
A measurement of the 1980
eclipse
(Dürst 1982) yields a radial slope proportional
to r-2.44 in the equator and r-2.76
at the poles when only
fitting the slope to the eclipse observations in the range from
2 to 10 .
Observations by Michard (1954) of the 1952
eclipse are fairly close
to the model corona suggested by Koutchmy & Lamy (1985),
whereas the Blackwell data and the
more recent observations by Dürst are a little lower.
Observations from the Apollo 16 spacecraft
describe the equatorial brightness beyond
20 as
(MacQueen et al. 1973).
We suggest to use for the visual spectral region a radial slope of the brightness as r-2.5 in the equator and r-2.8 at the pole (see Table 23 (click here)). This takes the recent measurements into account as well as the fact that the scattering properties change due to the increasing diffraction peak at small scattering angles.
Figure 58: The visible F-corona brightness, as measured along the ecliptic
and the polar meridian. Asterisks: Blackwell (1995) (1954 eclipse);
diamonds: Michard et al. (1954) (1952 eclipse);
triangles Dürst (1982); squares
Maihara et al. (1985). The power laws best representing
these data are shown as solid lines
< | region |
I( ) at 4  | radial slope |
|
(m) |
(W/m2srm) | ||
0.5 | equatorial | 2.8 10-2 | r-2.5 |
| polar | 1.8 10-2 | r-2.8 | |
| 2.12 | equatorial |  5 10-3 | r-1.9 |
| polar | 4 10-3 | r-2.3 |
W/m2srm.
Due to the difficulties of K-corona separation, mentioned above, the polarization of the F-corona brightness is not fully understood so far. Figure 60 (click here) describes some data of the polarization of the total visible F-coronal brightness together with two models of F-corona polarization.
The first case
is the polarization curve extrapolated from the Zodiacal light
polarization according to Eq. (16), the second case is the
polarization derived by Blackwell et al. (1967).
The classical coronal model
suggested in Blackwell et al. gives almost
no F-corona polarization within 
.
Furthermore, it has been suggested that
an irregular slope of the F-corona polarization could
either result from the beginning
of the dust free zone around the Sun
or reflect the existence
of a dust ring.
Observations
of the 1991 eclipse show no hump in the polarization
between 3 and 
and give an upper limit of
10% for the polarization.
Similar to the uncertainties in the determination of absolute brightness levels, the colour of the coronal brightness is not well defined (see Fig. 59 (click here)). Since both, thermal emission of dust as well as a spectral change of scattering properties cause a reddening of the F-corona (Mann 1993), we can expect reddening to vary within the corona. As far as the visible F-corona is concerned, several estimates of the colour are either describing only the inner corona or may be biased from uncertain calibrations. However it seems to be proven that the reddening is stronger than in the Zodiacal light and is also stronger than the reddening of the inner Zodiacal light extrapolated to smaller elongations (Koutchmy & Lamy 1985).
Figure 59: The equatorial F-corona brightness
at 4 . Diamonds: Maihara et al. (1985),
cross: Smartt (1973), triangles: MacQueen
(1968) (lower values), MacQueen &
Greeley (1995) (upper value); squares: Peterson (1967).
The dashed line gives the solar spectrum
normalized to wavelength
0.55 m
Figure 60: The polarization of the total
coronal brightness compared to the extrapolated
zodiacal light model and the F-corona
polarization according to
Blackwell et al. (1967)
Different values of the F-corona brightness at 4
in the near infrared are shown in Fig. 59 (click here)
in comparison to the solar spectral slope from Allen (1985),
normalized to the F-coronal brightness at 0.5 m. Although the
differences between data sets are still large, the majority
of data at longer wavelengths is above the extrapolated solar
spectrum, indicating a contribution from the thermal emission
of dust near the Sun.
Only the early infrared observations do not follow this trend.
The radial slope of the
near infrared F-corona brightness can be derived from
observations of the 1991 eclipse (Hodapp et al. 1992; Kuhn et
al. 1994; MacQueen et al. 1994),
however the sky conditions were mediocre, as mentioned above,
and no accurate photometry was possible.
The equatorial brightness was described as
and the polar brightness as 
,
for regions inside 8 .
Observations of the 1973 eclipse
by Smartt (1973) in the near-infrared ( = 1.03 m)
show a similar radial slope of r-1.9 between 
and 5
and of r-2.2 in the outer corona.
An important constituent
of interplanetary dust particles
is silicate, which exhibits a pronounced reststrahlen band
in the 10 m wavelength region.
An enhanced brightness of the mid infrared corona could reveal for instance the
presence of small silicate
particles near the Sun (cf. Kaiser 1970).
Unfortunately, data in the mid infrared regime are biased, either by
scattered light components from a window
in case of aircraft measurements
(Lena et al. 1974), or by strong atmospheric
emission and fluctuations in the case of observations
from ground (Mankin et al.\
1974).
The first measurement of the near infrared coronal brightness showed a deviation of the slope from a continuous increase within the corona, with brightness enhancements by a factor of 3 - 3.5. Several of these humps were seen by Peterson (1967) and MacQueen (1968), and later checked by Isobe et al. (1985), Mizutani et al. (1984), and Tollestrup et al. (1994). Model calculations by Mukai & Yamamoto (1979) showed that these humps could be explained by a dynamical effect that produces dust rings around the Sun. It is also possible that a hump of the infrared brightness is produced when the line of sight crosses the beginning of a dust free zone (Mann 1992). A model calculation by Kimura et al. (1997) shows that this effect may depend on the material composition of dust near the Sun. However, there have been several unpublished observations which could not detect a dust ring (see Isobe 1993), and observers of the 1991 eclipse could not confirm the existence of humps in the near infrared brightness (Hodapp et al. 1992; Kuhn et al. 1994; Tollestrup et al. 1994). In this context we should mention that the presently available data do not allow for a study of temporal effects in the F-coronal brightness, such as the appearance of dust clouds from sun-grazing comets or temporal dust rings.