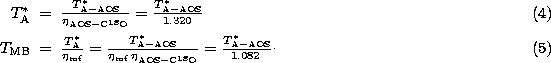The observations were carried out between the beginning of August 1993
and the end of August 1994. On Cerro Tololo, the Galactic center is
above an elevation of 20
for 11 hours per day. Because the
telescope cannot track sources at elevations higher than 78, the
total daily observing time was 9 hours.
The 
line was placed in the lower sideband of the
receiver because the line frequency is close to the lower limit of the
tuning range. With this, the image frequency of the system was
112.556165 GHz. The double-sideband receiver temperature,
, determined with a standard "Hot-Cold-Test''
using the filterbank backend, was always in the range of 180 to 220 K.
The radial velocity of the center channel of the AOS was set to
0 with respect to the Local Standard of Rest (LSR).
A detailed description of the observing procedure is given in Appendix A (click here). This includes the scan integration with weighted-OFFs position switching, the methods of scan calibration, and the telescope pointing.
Because the FWHM beam width of the telescope is 9
2 at the
line frequency, a fully sampled map requires
data spaced at 46. As a compromise to cover a larger region of
the Galactic center, we have used a grid spacing of 9
(=
0
15), that is half-sampling. We chose the grid axes to follow
Galactic coordinates centered on (
). Since
the 
emission is weak and the AOS was available only for a
limited time, we decided to concentrate on the inner region of the
Galactic center and to extend the map only to the Clump 2 region
(Bania 1977) in the range of l = +30 to +35.
Each position was observed with a series of 10-minute-scans. Typically, a single scan had an rms noise temperature per channel of about 0.12 to 0.15 K, with extremes from 0.08 to 0.25 K, on a scale, as obtained with the AOS (see Sect. 3.4.2 (click here)). The scans were averaged until the rms noise temperature per channel in the average spectrum was less than 0.05 K. Typically, twelve 10-minute-scans per position were needed to reach this limit, and on average 0.04 K was reached. Thus, two to three positions per day could be completely measured.
This long total integration time was necessary to reach a reasonable
signal-to-noise ratio in the spectra. The most intense
emission, at SgrB2, is only 0.45 K, i.e. for
this source, the maximum signal-to-noise ratio per channel was about
10. Away from this peak the emission decreases quickly to about 0.2 K
peak temperature and outside the inner region to below the 
detection limit of 0.15 K. At many grid positions
emission is only detected by integrating over a
number of velocity channels.
The OFF positions used, verified to be free of
emission stronger than 0.04 K, are given in
Appendix B (click here). Since these OFF positions are
appropriate for observations, they are very well
suited for measurements of the much weaker
emission.
Each spectrum was examined individually, and bad spectrometer channels, difficult to avoid on a CCD chip with 1499 channels, were removed and replaced by interpolating the neighbouring channels. After this cleaning, all spectra of the same position were averaged, the regions for the baseline subtraction were selected and a polynomial baseline was subtracted. By inspecting every single spectrum individually we checked for artefacts which might mimic emission in the averaged spectrum. Such features occur rarely. These were not considered to be emission but rather as instrumental baseline effects contributing to the uncertainties.
Figure 2: The averaged spectrum of 13 individual 10-minute-spectra
toward the position l = 075, b = -015 of the
Galactic Center Survey. The line windows and
the 
order baseline are also displayed. The
rms of the fit of the baseline to the spectrum is 0.047 K
The reduction procedure was as follows: If the noise in all spectra was
roughly the same, as was the case for most positions, the spectra were
first averaged, weighted by time, i.e. equally. Then, the regions for
the baseline subtraction were selected. The average spectrum was used
for this selection, because here weak line emission could be recognized
more easily and, therefore, the window regions, where the channel
content could not be used for the baseline fit, could be set
accordingly. In cases of uncertainty these windows were determined by
comparison with spectra. If the noise of
individual spectra for one position was significantly different, first,
the line windows were set in a provisional average of the spectra.
Then, baselines were subtracted from the individual spectra and these
spectra were averaged, weighted by the rms per channel, determined
from the baseline fit. Finally, a baseline of order 0 was subtracted
from the average spectrum. We have checked that averaging weighted by
rms did not have any effect on the intensity and line shape
compared to averaging weighted by time. Such an average yielded lower
rms per channel only if the noise of the single spectra
contributing to one position was significantly different.
The polynomial baseline subtracted was typically of order 6 with long
"periods'' (
) and low amplitudes (
).
This baseline was caused by standing waves from reflections in the
telescope. The FWZI extent of the emission is typically 50 to
250 , which is less than in 
. In addition, the FWHP width
of individual emission features are typically about 30 to
60 which is one order of magnitude less than the period of the
subtracted baseline. Therefore, we found that the baselines and
emission were clearly distinguishable and we could ascertain
that the order baselines do not affect the intensities of
the 18 emission systematically nor introduce artefacts. In
Fig. 2 (click here), we show a typical example of an averaged
spectrum with the chosen emission regions and the subtracted baseline
of order.
Figure 3: The integrated intensity of the innermost 
- and
b = -015-positions of the Galactic center region which were
measured twice. The open squares represent the results of August 1993,
the crosses the results of March 1994. The positions at b =
-015 are plotted with their l value reduced by 005
To check that the observations were reproduceable the innermost
positions of the Galactic center region (l = -015 to 135,
b = -015 to 00), which were first observed in August
1993, were remeasured in March 1994. In Fig. 3 (click here), the
integrated intensities, 
, from both
observing periods are compared for the velocity ranges from -373.7
to -225.0, from -225.0 to +225.0, and from +225.0 to
+373.7 which represent the emission of the
) line, the emission of the
line, and an emission-free region,
respectively. These plots show that the observations were reproducible
within a certain scatter and that no time-dependent systematic changes
were present in the data. A good measure for the scatter is the mean
deviation of the integrated intensity of the two periods which is given
by:
where Ii is the integrated intensity of position i. The average
value of this mean deviation, 
, is given in
Table 1 (click here) and compared to the expected value,
, from the average rms per channel, 0.04 K,
determined by:
where 
is the number of channels covered by the integration
area and 
is the channel width. From this comparison, it
becomes clear that in the emission-free area the scatter is within the
expected limit whereas in the areas containing emission it is larger.
This indicates that the uncertainties of the integrated intensities in
areas of emission is mostly caused by uncertainties in the baselines
and that the rms noise per channel plays a minor role. The reason
for the rather strong influence of the baseline choice on the
integrated intensity is that the observed emission lines are rather
weak but have extended wings. Therefore, a small error in the baseline
causes a relatively large error in the integrated intensity. This
effect is even larger for the ) line
due to additional uncertainties caused by this line being at the edge
of the frontend and backend bands. It illuminates the necessity of
having not only a sensitive system but also a stable system with flat
baselines when broad lines are observed (see also Radford et
al. 1996 for an analysis of baseline problems when observing broad,
in their case extragalactic, lines).
| Velocity range | Line |
 |  | ||
| K | K | ||||
| -373.7 | - | -225.0 | HNCO | 7.10 | 0.84 |
| -225.0 | - | +225.0 | C18O | 5.42 | 1.45 |
| +225.0 | - | +373.7 | -- | 0.25 | 0.84 |
The calibration of the scans follows the standard chopper wheel method first described by Penzias & Burrus (1973) and applied at many other millimeter telescopes. See Appendix A.2 (click here) for a detailed description of this method.
In addition to daily antenna tippings, the calibration stability was
monitored by taking a 10-minute-spectrum toward the position l =
0625, b = 00 (SgrB2) once or twice per day. With a
peak temperature of 1.14 K, the ) line
is considerably stronger than the line (0.45 K)
toward this position and its intensity, integrated over a velocity
range from -322.0 to -245.0 (with respect to the
line frequency) is a good indicator for the
calibration stability.
The stability of the calibration, throughout the course of the survey,
proved to be excellent (better than 1% on different days), and the
mean uncertainty in the calibration of a single scan is 
.
For 12 scans, the typical number of scans per position, the calibration
uncertainty just from statistics is 
and probably better,
because a large part of the calibration uncertainty is caused by the
uncertainty in the determination of the baseline which was much better
determined in the averaged spectrum (see also Sect. 3.3 (click here)).
The chopper wheel method calibrates the signal coming out of the
backend to the antenna temperature, . This calibration bases on
the scaling factor 
(see Appendix A.2 (click here)),
which, for instrumental reasons, could be determined only with the
filterbank. Because the signal path to the AOS differed from that to
the filterbank, the response of the two backends was not equal.
Therefore, as a last step in the calibration process, the correct
scaling of the spectra taken with the AOS to , the AOS
"efficiency'', had to be determined. The effect of different response
could be seen most clearly toward positions where the
line emission was narrow enough and close enough
to = 0 to be also observed with the filterbank. A
comparison of more than 150 spectra, taken simultaneously with the AOS
and the filterbank toward 13 different positions, yielded a ratio of
peak antenna temperatures between the AOS and the filterbank, resampled
to the resolution of the AOS, of 
, and a ratio of 
for integrated intensities (see Dahmen 1995 for
more details).
However, to finally determine the different scaling factor of the AOS
it is necessary to compare an emission feature of the AOS, which is
well resolved and which lies well above the detection limit, with the
result of an observation toward the same position with the same
beamwidth and with comparable frequency resolution the calibration of
which is well known. Obviously, SgrB2 (l=0625, b=00)
is a suitable position for this purpose. SgrB2 was observed in
with the 0.5 MHz-resolution-filterbank at the
1.2m NMWT during November 1994. This telescope has the same beamwidth
as the SMWT and the calibration is well established (Cohen
et al. 1986). Because the scaling factor from to ,
, is the same for both
telescopes (see Appendix A.2 (click here)) the values could be
compared directly. This comparison was done using peak intensities instead
of integrated intensities because a significant part of the integrated
intensity originates in the extended wings of the broad line. Thus,
small errors in the baseline give rise to larger errors in the
integrated intensity, since the integrated intensity is the product of
the velocity window and the average intensity in this window. An
identical absolute baseline error is translated to a larger relative
error if related to the average intensity than if related to the peak
intensity. In both spectra, the peak intensity was fitted, with a
Gaussian curve. With these fits, the "efficiency'' of the AOS
calibration at the line emission,
, is:
This value is, within the noise, the same as the one determined by
comparing spectra obtained with the AOS with spectra obtained with the
FB at the 1.2m SMWT. Thus, the main (and probably single) cause for
scaling differences between spectra taken with the SMWT and the 1.2m
NMWT is the integration of the AOS into the system of the SMWT. The
calibration of the SMWT filterbank is identical to within the noise
with the calibration obtained at the NMWT, and the following final
conversions for and can be established:
