The immediate result of this paper is the catalogue of 595 mean radial
velocities and derived quantities contained in Tables 1 and 2 (click here). As shown in
Fig. 3 (click here), the typical mean error of the mean velocity of a constant star is 
1
km s-1 for stars rotating less than 120 km s-1.
As our criterion for identifying spectroscopic binaries in the sample we adopt
the limit 
0.01 for significant radial-velocity variability,
i.e. a confidence level of 99%. The distribution of observed 
values is displayed in Fig. 4 (click here) and shows a prominent peak of 170 stars in the bin
0.00 - 0.01 in , corresponding to the spectroscopic binaries. It is
also noteworthy, however, that the distribution remains essentially
flat in the entire range 0.01 - 1.00, indicating that the internal error
estimates from XCSAO which were used to compute 
are indeed realistic.
If one relaxes the variability criterion to 0.04, the
number of stars satisfying this criterion increases to 199.
The bins 0.00 - 0.04 in Fig. 4 (click here) still contain a random component of constant
stars, corresponding to the average level in the rest of the
range, 4.1 stars per bin of 0.01 in . Hence, the 170 stars in the
first bin should be reduced to 166, and the 29 stars in the next three bins to
17, giving a range for the true number of detected binaries of 166 - 182, with
a sampling error of 13. The observed binary frequency is thus 29 
2%.
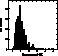
Figure 3: Distribution of mean errors (km s-1) of the mean velocities of the 426 constant
stars from Table 1 (defined by the criterion 
0.01
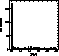
Figure 4: Distribution of observed values for all stars in Tables 1 and 2
with more than one observation (bin size 0.01)
The raw binary fraction derived above must be corrected for the fact that our
sample is limited by apparent magnitude, thus favouring the inclusion of
binaries which are, on average, more luminous than the single stars. Suppose,
as an example, that our double-lined binaries (Table 2 (click here)) were on average 50% more
luminous than single stars of the same colour. We would then include them from a
volume that is a factor 1.84 larger than that in which the single stars are complete.
Under this assumption, 30 of these stars would be removed from the sample
for this reason, reducing the true frequency of detected binaries to 24 2%.
A similar effect will operate on the 100 single-lined systems since the light
of the secondaries will be present at some level, but we estimate that 10%
is a plausible rough upper limit to their contribution. This suggests that fewer
than 15 single-lined binaries have been included from outside our
completeness limit for single stars, reducing our estimate of the true frequency
of detected binaries to perhaps 22 2%.
A similar analysis of the distribution of the
Duquennoy & Mayor
(1991) volume-limited sample of G dwarfs (their Fig. 3 (click here)) yields a fraction of
radial-velocity variables of 37%. If the true frequency of spectroscopic
binaries is the same in the two samples, these figures suggest that we have
missed about half of the total number of spectroscopic binaries in our own
sample. This is to be expected because the detection limit for velocity
variability is significantly higher for our fast-rotating F stars, and the time
span and number of observations per star are rather lower than in the study by
Duquennoy & Mayor.
The 24 double-lined systems consisting of a rapidly-rotating late A star and a sharp-lined cooler secondary are of special interest. As their combined uvby indices mimic those of the youngest, early F-type dwarfs, these stars would have appeared in that age group if their binary nature had gone unnoticed. Their derived metallicity would also have been affected by their composite nature, biasing the resulting age-metallicity diagram (AMD).
It has recently been proposed (Wielen et al. 1996) that the scatter in the AMD is the result of diffusion of disk star orbits. According to their model, the true birthplace of a star can be derived from its position in the AMD under the assumption of a single-valued local age-metallicity relation (AMR) and a radial abundance gradient in the disk: The farther a star is off the mean relation, the farther from the solar circle was it supposedly born. As a specific example, since the [Fe/H] of the Sun is 0.17 dex higher than the average for nearby F dwarfs of the same age, it would supposedly have been formed at a galactocentric distance of 6.6 kpc. According to this theory, its orbit would then have been modified by interactions with massive objects in the disk (perhaps giant molecular clouds or massive black holes) so that it reached its present mean distance at R0 = 8.5 kpc after 4.6 Gyr, and with its orbital eccentricity modified again to near its presumably small initial value.
When using F stars to test such an hypothesis (see Nordström et al. 1997), early F stars with high or low abundances are particularly important since they have had the least time to diffuse into the solar neighbourhood from their putative distant birthplaces. Even a few spurious points in the AMD due to unrecognised binaries of the type discussed above could lead to erroneous conclusions. The data presented here will help to avoid such mistakes.
Acknowledgements
The grid of synthetic template spectra computed by Jon Morse, with the model atmosphere programmes and spectral line lists by Robert Kurucz, were key elements in the work presented here, as were the XCSAO package and TODCOR implementations by our CfA colleagues. Financial support to BN and JA from the Carlsberg Foundation, the Danish Natural Science Research Council, and the Smithsonian Institution is gratefully acknowledged.