Echelle spectra for all programme stars were obtained with the 1.5-m Wyeth reflector at the Oak Ridge Observatory in Harvard, Massachusetts, the 1.5-m Tillinghast reflector on Mt. Hopkins, Arizona, and occasionally with the Multiple Mirror Telescope, also at Mt. Hopkins. Echelle spectra covering the range 5165.77-5211.25 Å were obtained with the nearly identical CfA echelle spectrograph systems at all three telescopes and recorded with photon-counting intensified Reticon detectors. The instruments and standard observing and reduction procedures are described by Latham (1985, 1992). Standard observing procedures were followed throughout, but with increased exposure levels for the more rapidly-rotating stars which need better signal-to-noise in order to ensure reliable velocities.
For the determination of radial velocities from these spectra for stars
with a wide range of rotations, we have developed a digital cross-correlation
procedure based on the XCSAO task (Kurtz et al. 1992) as implemented in the
IRAF environment
, using a large grid of synthetic template spectra covering
the ranges in effective temperature, gravity, and rotation of our programme
stars. The details of our technique and its performance have been documented in
Paper I and will not be repeated here. We comment briefly below on its practical
application to the programme stars, and on two refinements in the technique
implemented since Paper I.
The grid of synthetic template spectra used here was computed for [Fe/H] = 0.0, as the m1 index for the programme stars indicated that they all have metallicities sufficiently close to solar. Effective temperatures range from 6000 to 7000 K in steps of 250 K, log g from 4.5 to 3.0 in steps of 0.5 dex, and v sin i from 0 to 100 km s-1 in steps of 10 km s-1 and from 100 to 200 km s-1 in steps of 20 km s-1. Optimum templates were selected for the individual programme stars as follows:
For the stars with known H
indices and reddenings (about 3/4 of the
sample), Dr. E.H. Olsen kindly computed the individual 
and log g values,
using the Magain (1987) calibration for and a procedure similar to that
of Edvardsson et al. (1993) for log g. The set of templates closest to these
values was selected for each of these stars. For the remainder, we assumed
= 7000 K and log g = 4.0 as our previous tests have shown these to be adequate
(Paper I).
The optimum template rotation cannot be defined from the photometry, but must be found from test correlations of the observed spectra with the appropriate set of rotating templates. In Paper I, optimum template selection was based on the goodness-of-fit parameter R (cf. Kurtz et al. 1992). As noted there, however, this criterion fails in the numerous cases of composite spectra. Considerable further experimentation led us to the conclusion that the maximum height of the correlation peak is a more reliable criterion for choosing the rotating template which gives the best match to the observed spectra, and this method was adopted for the final correlations of all programme stars.
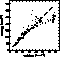
Figure 1: Rotational velocities (km s-1) derived here vs. those observed with CORAVEL
From the correlation peak height as a function of template rotation, the
value corresponding to maximum correlation height was estimated by quadratic
interpolation. As shown in Fig. 1 (click here), this procedure leads to much better agreement
with the CORAVEL rotations measured for the overlap of slowly-rotating stars
common to the two programmes which was discussed in Paper I. The overall
zero-point and scale differences in v sin i seen with the older procedure have
disappeared, although there still seems to be a difference of 
3 km s-1
for rotations around 20 km s-1. Given the uncertainties in the treatment of the
instrumental profile and scattered light of our data and the simplifying
assumptions underlying the calibration of both methods, the origin of this
difference is not clear, but it remains within the fundamental uncertainty of
10% derived by Collins & Truax (1995). The increased scatter seen for
v sin i > 40 km s-1 is presumably due to the rapidly deteriorating accuracy of
the CORAVEL rotations for such broad-lined stars, due to the fixed CORAVEL mask
which is optimised for sharp-lined stars.
We have verified that our radial-velocity zero-point, which was the key subject of Paper I, remains the same to within 100 m s-1 when using this modified procedure. Thus, our previous results on the systematic and random errors of our radial velocities remain valid for the data presented here.
The second refinement in our technique was the use of the two-dimensional cross-correlation algorithm TODCOR (Zucker & Mazeh 1994), as implemented at CfA by G. Torres, to extract radial velocities of both components from the observed, blended spectra of 65 double-lined spectroscopic binaries in our sample. For 18 of these systems we had enough velocities to allow solutions for double-lined orbits, and in another 21 cases the available pairs of primary and secondary velocities spanned a sufficient velocity range that we could use the Wilson (1941) method to derive systemic velocities and mass ratios.
The ability of TODCOR to extract reliable velocities even from strongly blended correlation peaks is quite remarkable, if a suitably fine grid of rotating templates is available. The absence of systematic velocity errors has been checked in a system with equal components by Latham et al. (1996). As an application of particular value in the present programme, we have been able to derive velocities with TODCOR for a considerable number of systems composed of rapidly-rotating late A-type primaries and sharp-lined late-type secondaries contributing only a few percent of the total light. For these systems the standard correlations against slowly-rotating templates only picked up the velocity of the slowly-rotating secondary. With TODCOR we were able to identify the spectrum of the rapidly-rotating primary and to solve for the velocities of both stars.
TODCOR can also provide an estimate of the light ratio L2/L1 between the two stars at the wavelength observed. We list this information when available, but have not performed a similarly exhaustive study of its accuracy as for the radial velocities, including, e.g., template optimization for the individual binary components.