

Up: Method of running
If the input signal is sinusoidal:

then the corresponding smoothing curve is

where  and
and

Asymmetric fits change not only the amplitude, but the phase as well.
Such phase distortions occur at the temporal edges of the observations.
For intermediate values of the argument, z1=-1 and z2=1.
Because of the symmetry of the function 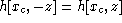 , in this
case
, in this
case  for all
for all  .
.

Figure 4: Dependence of the amplitude of the harmonic fit
smoothing a model sine function of unit amplitude and a period P
on 
For our test symmetric fits,

These functions are shown in Fig. 4 (click here).
A function 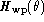 crosses zero at the value
crosses zero at the value  ,
much larger as compared with
,
much larger as compared with  corresponding to a zero of
corresponding to a zero of
 . Some useful values of
. Some useful values of  are 0.7047 and
0.8553, which correspond to
are 0.7047 and
0.8553, which correspond to  and 1/2,
respectively.
and 1/2,
respectively.
The power spectra S(x(t),f) of the smoothed signal are proportional
to r2 (e.g. Box & Jenkins 1970), thus for harmonic signal with
frequency
f=1/P one may obtain 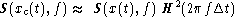 .
However, for the deviations from the fit
.
However, for the deviations from the fit

At high frequencies 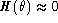 , thus fast variations are not
affected by removal of a "slow trend" such as the slope
, thus fast variations are not
affected by removal of a "slow trend" such as the slope  of the
power spectra
of the
power spectra  detected in some cataclysmic variables
(Andronov 1993). Applications corresponding to the integer values
detected in some cataclysmic variables
(Andronov 1993). Applications corresponding to the integer values
 are described by Terebizh (1992). Influence of the trend
removal on the shape of the autocorrelation function (ACF) was studied
by Andronov (1994).
are described by Terebizh (1992). Influence of the trend
removal on the shape of the autocorrelation function (ACF) was studied
by Andronov (1994).
The functions  cross zero for all fits with finite z1 and
z2. The "ideal" "rectangular" shape H=1, if
cross zero for all fits with finite z1 and
z2. The "ideal" "rectangular" shape H=1, if 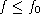 corresponds
to an "ideal low frequency" signal
corresponds
to an "ideal low frequency" signal  usually described in radiotechnics (e.g. Baskakov 1983). Here
usually described in radiotechnics (e.g. Baskakov 1983). Here

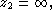
 . For real functions
. For real functions 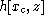 limiting values of z are finite, causing for some frequencies the
negative values of
limiting values of z are finite, causing for some frequencies the
negative values of  . In this case, the "output" smoothing
function is in anti-phase with the "input" signal, thus the difference
. In this case, the "output" smoothing
function is in anti-phase with the "input" signal, thus the difference
 will have even larger amplitude than the "true" one.
The maximum "amplification" occurs for 4 tested methods at
will have even larger amplitude than the "true" one.
The maximum "amplification" occurs for 4 tested methods at 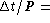 0.715, 1.112, 1.112, 1.489 with corresponding values of
0.715, 1.112, 1.112, 1.489 with corresponding values of 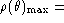 1.4816, 1.0839, 1.5421, 1.1446. For the "white noise", mathematical
expectation of the amplitude does not depend on frequency, thus a power
spectrum of the detrended observations may show an apparent peak due to
negative values of
1.4816, 1.0839, 1.5421, 1.1446. For the "white noise", mathematical
expectation of the amplitude does not depend on frequency, thus a power
spectrum of the detrended observations may show an apparent peak due to
negative values of 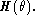 For symmetric approximations, values of
For symmetric approximations, values of
 are much smaller for weighted fits, than for
unweighted. Case "wp" is not significantly worse than "wm" according
to this criterion, but has a strong advantage due to wider shape of
are much smaller for weighted fits, than for
unweighted. Case "wp" is not significantly worse than "wm" according
to this criterion, but has a strong advantage due to wider shape of
 .
.
For noisy sinusoidal signal  and a "continuous"
approximation one may estimate a "signal/noise" ratio
and a "continuous"
approximation one may estimate a "signal/noise" ratio

where  , r0 is the amplitude of a harmonic component and
, r0 is the amplitude of a harmonic component and
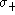 is an accuracy estimate of an individual values which may be
set to
is an accuracy estimate of an individual values which may be
set to 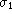 . For fixed n
(number of observations per period P), this ratio increases with
increasing
. For fixed n
(number of observations per period P), this ratio increases with
increasing 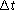 proportionally to
proportionally to  (as the number of the
observations inside an interval increases). However, for large
(as the number of the
observations inside an interval increases). However, for large 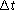 , the
amplitude of the smoothed function decreases
, the
amplitude of the smoothed function decreases  . Thus
exists an "optimal" value of
. Thus
exists an "optimal" value of  where "signal/noise" reaches its
maximum. For continuous approximation, this occurs at
where "signal/noise" reaches its
maximum. For continuous approximation, this occurs at  0.1855,
0.2895, 0.4123, 0.5450 for 4 fits with corresponding
0.1855,
0.2895, 0.4123, 0.5450 for 4 fits with corresponding  0.7885,
0.7843, 0.8749, 0.8716 and a value
0.7885,
0.7843, 0.8749, 0.8716 and a value  0.3396, 0.3531, 0.37450, 0.38353. This factor decreases by
0.3396, 0.3531, 0.37450, 0.38353. This factor decreases by  times at
times at 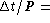 0.0608, 0.0936, 0.1589, 0.2093, i.e. there is a long
enough nearly "standstill", if "signal/noise" is plotted vs.
0.0608, 0.0936, 0.1589, 0.2093, i.e. there is a long
enough nearly "standstill", if "signal/noise" is plotted vs.  .
.
In other words, approximations by a parabola give better results than
that by a constant, the "optimal" fit corresponding to "wp" allowing to
use more wide intervals than other fits.
Estimates of extremum time errors are possible only for m>0, as

Minimum of this function for fits "up" and "wp" occurs at 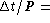 0.5515
and 0.7440 with corresponding
0.5515
and 0.7440 with corresponding 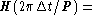 0.6725 and 0.65669 and
values 0.15929 and 0.2928
0.6725 and 0.65669 and
values 0.15929 and 0.2928  . Here an accuracy estimate for
"wp" is worse than for "up". But "up" fit is a discontinuous fit, and
sometimes its derivative may be infinite. The accuracy estimate is twice
larger than an "optimal" value at
. Here an accuracy estimate for
"wp" is worse than for "up". But "up" fit is a discontinuous fit, and
sometimes its derivative may be infinite. The accuracy estimate is twice
larger than an "optimal" value at 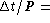 0.2712, 0.3612.
0.2712, 0.3612.
For small noise  which is comparable with
which is comparable with  and/or discrete
signal one may determine numerically the parameter
and/or discrete
signal one may determine numerically the parameter  optimizing a
fixed characteristic.
optimizing a
fixed characteristic.


Up: Method of running
Copyright by the European Southern Observatory (ESO)
web@ed-phys.fr

