In Tables 1 (click here), 2 (click here) and 3 (click here), we display the f-values obtained in the present work together with theoretical values reported by other authors, given that no experimental measurements have been found in the literature. In the figures we show the systematic trends that some of the studied oscillator strengths present for individual transitions along the isoelectronic sequence when they are plotted versus the inverse of Z.
For ![]() transition we have
performed both RQDO and MCDF calculations. Inspection of Table 1 (click here) shows that
our oscillator strengths compare generally well with the f-values
calculated by Biémont (1986a, 1986b), who combined the
self-consistent field (HXR) method of Cowan (1981), which
explicitly accounts for configuration interaction and some relativistic
effects for obtaining the wave functions with a semiempirical fitting
procedure for obtaining the energy eigenvalues. Biémont reports f-values
(1986a) for the first few ions of the sequence only. Our RQDO f-values
take explicitly into account core-polarization effects. It should be born
in mind that some of the levels involved in the transition can be subjected
to perturbations by other levels, as pointed out by Biémont
(1986a). These perturbations are explicitly accounted for in the
MCDF calculations. In the RQDO procedure, the effect of perturbations is
only implicitly included through the quantum defects extracted from
experimental energies. Overall, the RQDO f-values agree reasonably well
with the MCDF results and these by Biémont (1986a, 1986b),
both expected to be correct. A source of discrepancy between the RQDO and
HXR (Biémont 1986a) f-values is, quite possibly, the use of
different energy data. Both the RQDO and MCDF results, as well as the HXR
f-values, comply with the general feature which characterises an LS
coupling scheme (Cowan 1981), in all ions comprised in
Table 1 (click here), of reflecting that the strongest transitions are those
corresponding to
transition we have
performed both RQDO and MCDF calculations. Inspection of Table 1 (click here) shows that
our oscillator strengths compare generally well with the f-values
calculated by Biémont (1986a, 1986b), who combined the
self-consistent field (HXR) method of Cowan (1981), which
explicitly accounts for configuration interaction and some relativistic
effects for obtaining the wave functions with a semiempirical fitting
procedure for obtaining the energy eigenvalues. Biémont reports f-values
(1986a) for the first few ions of the sequence only. Our RQDO f-values
take explicitly into account core-polarization effects. It should be born
in mind that some of the levels involved in the transition can be subjected
to perturbations by other levels, as pointed out by Biémont
(1986a). These perturbations are explicitly accounted for in the
MCDF calculations. In the RQDO procedure, the effect of perturbations is
only implicitly included through the quantum defects extracted from
experimental energies. Overall, the RQDO f-values agree reasonably well
with the MCDF results and these by Biémont (1986a, 1986b),
both expected to be correct. A source of discrepancy between the RQDO and
HXR (Biémont 1986a) f-values is, quite possibly, the use of
different energy data. Both the RQDO and MCDF results, as well as the HXR
f-values, comply with the general feature which characterises an LS
coupling scheme (Cowan 1981), in all ions comprised in
Table 1 (click here), of reflecting that the strongest transitions are those
corresponding to ![]() , in the two groups of
triplet-triplet transitions which correspond, respectively, to the first
three and last three columns of the table.
, in the two groups of
triplet-triplet transitions which correspond, respectively, to the first
three and last three columns of the table.
| Z | ION | M | ||||||
| 19 | KVI | a. | 0.1352 | 0.0468 | 0.0337 | 0.0569 | 0.0360 | 0.1041 |
| b. | 0.1724 | 0.0581 | 0.0433 | 0.0706 | 0.0436 | 0.1280 | ||
| c. | 0.1413 | 0.0482 | 0.0349 | 0.0621 | 0.0372 | 0.1099 | ||
| 20 | CaVII | a. | 0.1337 | 0.0467 | 0.0332 | 0.0565 | 0.0362 | 0.1031 |
| b. | 0.1709 | 0.0577 | 0.0430 | 0.0698 | 0.0433 | 0.1267 | ||
| c. | 0.1380 | 0.0482 | 0.0333 | 0.0607 | 0.0364 | 0.1074 | ||
| 21 | ScVIII | a. | 0.1306 | 0.0460 | 0.0323 | 0.0554 | 0.0361 | 0.1009 |
| b. | 0.1695 | 0.0573 | 0.0427 | 0.0690 | 0.0431 | 0.1253 | ||
| c. | 0.1349 | 0.0460 | 0.0318 | 0.0593 | 0.0364 | 0.1026 | ||
| 22 | TiIX | a. | 0.1271 | 0.0451 | 0.0312 | 0.0541 | 0.0361 | 0.0982 |
| b. | 0.1678 | 0.0568 | 0.0423 | 0.0680 | 0.0427 | 0.1238 | ||
| c. | 0.1288 | 0.0450 | 0.0304 | 0.0566 | 0.0364 | 0.0980 | ||
| 23 | VX | a. | 0.1235 | 0.0443 | 0.0300 | 0.0528 | 0.0362 | 0.0952 |
| b. | 0.1706 | - | 0.0430 | 0.0690 | 0.0435 | 0.1257 | ||
| 24 | CrXI | a. | 0.1202 | 0.0434 | 0.0289 | 0.0516 | 0.0375 | 0.0921 |
| b. | 0.1697 | 0.0576 | 0.0429 | 0.0685 | 0.0434 | 0.1248 | ||
| 25 | MnXII | a. | 0.1172 | 0.0427 | 0.0279 | 0.0504 | 0.0372 | 0.0888 |
| b. | 0.1683 | - | 0.0426 | 0.0677 | 0.0431 | 0.1234 | ||
| 26 | FeXIII | a. | 0.1144 | 0.0420 | 0.0269 | 0.0493 | 0.0380 | 0.0853 |
| b. | - | 0.0581 | - | 0.0664 | - | 0.1212 | ||
| 27 | CoXIV | a. | 0.1119 | 0.0414 | 0.0260 | 0.0483 | 0.0390 | 0.0816 |
| b. | 0.1512 | - | 0.0384 | 0.0660 | 0.0390 | 0.1207 | ||
| 28 | NiXV | a. | 0.1097 | 0.0408 | 0.0252 | 0.0473 | 0.0402 | 0.0778 |
| b. | - | - | - | 0.0642 | - | 0.1196 | ||
| 29 | CuXVI | a | 0.1078 | 0.0403 | 0.0245 | 0.0465 | 0.0414 | 0.0738 |
| b. | 0.1607 | 0.0551 | 0.0410 | 0.0636 | 0.0415 | 0.1162 | ||
| 30 | ZnXVII | a | 0.1060 | 0.0399 | 0.0239 | 0.0456 | 0.0427 | 0.0698 |
| b. | 0.1586 | 0.0546 | 0.0406 | 0.0620 | 0.0412 | 0.1135 | ||
| 31 | GaXVIII | a | 0.1044 | 0.0395 | 0.0233 | 0.0449 | 0.0439 | 0.0658 |
| b. | 0.1514 | 0.0523 | 0.0389 | 0.0588 | 0.0395 | 0.1077 | ||
| 32 | GeXIX | a | 0.1030 | 0.0392 | 0.0228 | 0.0442 | 0.0451 | 0.0619 |
| b. | 0.1496 | 0.0518 | 0.0385 | 0.0579 | 0.0392 | 0.1060 | ||
| 33 | AsXX | a | 0.1016 | 0.0389 | 0.0223 | 0.0435 | 0.0462 | 0.0582 |
| b. | 0.1496 | 0.0519 | 0.0386 | 0.0577 | 0.0392 | 0.1056 | ||
| 34 | SeXXI | a | 0.1004 | 0.0387 | 0.0219 | 0.0429 | 0.0472 | 0.0548 |
| b. | 0.1486 | 0.0517 | 0.0385 | 0.0571 | 0.0391 | 0.1046 | ||
| 35 | BrXXII | a | 0.0993 | 0.0385 | 0.0216 | 0.0424 | 0.0481 | 0.0516 |
| b. | 0.1511 | 0.0526 | 0.0392 | 0.0581 | 0.0398 | 0.1063 | ||
| 36 | KrXXIII | a | 0.0982 | 0.0383 | 0.0213 | 0.0419 | 0.0489 | 0.0487 |
| b. | 0.1477 | 0.0516 | 0.0384 | 0.0565 | 0.0390 | 0.1033 | ||
| 37 | RbXXIV | a | 0.0972 | 0.0382 | 0.0211 | 0.0414 | 0.0496 | 0.0461 |
| b. | 0.1353 | 0.0476 | 0.0354 | 0.0509 | 0.0360 | 0.0933 | ||
| 38 | SrXXV | a | 0.0962 | 0.0381 | 0.0208 | 0.0409 | 0.0503 | 0.0437 |
| b. | 0.1338 | 0.0472 | 0.0351 | 0.0502 | 0.0357 | 0.0918 | ||
| Z | ION | M | ||||||
| 39 | YXXVI | a | 0.0953 | 0.0380 | 0.0207 | 0.0405 | 0.0508 | 0.0416 |
| b. | 0.1388 | 0.0490 | 0.0365 | 0.0523 | 0.0370 | 0.0956 | ||
| 40 | ZrXXVII | a | 0.0944 | 0.0380 | 0.0205 | 0.0400 | 0.0514 | 0.0397 |
| b. | 0.1473 | 0.0518 | 0.0387 | 0.0560 | 0.0391 | 0.1023 | ||
| 41 | NbXXVIII | a | 0.0936 | 0.0380 | 0.0204 | 0.0396 | 0.0519 | 0.0380 |
| b | 0.1481 | 0.0521 | 0.0389 | 0.0563 | 0.0394 | 0.1027 | ||
| 42 | MoXXIX | a. | 0.0928 | 0.0380 | 0.0203 | 0.0393 | 0.0524 | 0.0365 |
| b | 0.1478 | 0.0521 | 0.0389 | 0.0554 | 0.0393 | 0.1010 | ||
| 44 | RuXXXI | a. | 0.0914 | 0.0382 | 0.0202 | 0.0386 | 0.0534 | 0.0339 |
| b | 0.1213 | 0.0436 | 0.0325 | 0.0435 | 0.0330 | 0.0795 | ||
| 45 | RhXXXII | a. | 0.0907 | 0.0383 | 0.0201 | 0.0383 | 0.0538 | 0.0328 |
| b. | 0.1220 | 0.0439 | 0.0328 | 0.0435 | 0.0332 | 0.0794 | ||
| 46 | PdXXXIII | a. | 0.0900 | 0.0384 | 0.0201 | 0.0380 | 0.0543 | 0.0318 |
| b. | 0.1239 | 0.0446 | 0.0333 | 0.0439 | 0.0337 | 0.0802 | ||
| 47 | AgXXXIV | a. | 0.0894 | 0.0385 | 0.0201 | 0.0377 | 0.0547 | 0.0309 |
| b. | 0.1280 | 0.0458 | 0.0342 | 0.0450 | 0.0347 | 0.0821 | ||
| 48 | CdXXXV | a. | 0.0887 | 0.0387 | 0.0202 | 0.0374 | 0.0552 | 0.0301 |
| b. | 0.1312 | 0.0471 | 0.0352 | 0.0463 | 0.0355 | 0.0842 | ||
| 49 | InXXXVI | a. | 0.0882 | 0.0389 | 0.0202 | 0.0372 | 0.0557 | 0.0294 |
| 50 | SnXXXVII | a. | 0.0876 | 0.0391 | 0.0202 | 0.0369 | 0.0562 | 0.0287 |
| 51 | SbXXXVIII | a. | 0.0870 | 0.0393 | 0.0203 | 0.0367 | 0.0567 | 0.0281 |
| 52 | TeXXXIX | a | 0.0865 | 0.0395 | 0.0204 | 0.0364 | 0.0572 | 0.0275 |
| 53 | IXL | a | 0.0860 | 0.0398 | 0.0205 | 0.0362 | 0.0577 | 0.0270 |
| 54 | XeXLI | a | 0.0855 | 0.0401 | 0.0206 | 0.0360 | 0.0583 | 0.0265 |
In Table 2 (click here), we compare our two sets of f-values for the ![]() transition with a few theoretical results,
which seem to be the only data available in the literature. For the first
four ions, it is possible to compare our oscillator strengths with data
reported by Biémont, using the same HXR method as in the above transition
(Biémont 1986a), and with the f-values obtained with the
length and velocity forms of the dipole transition operator by Nahar &
Pradham (1993) within the Opacity Project. Their method of
calculation, the close coupling (CC) aproximation using the R-matrix method,
explicitly accounts for configuration interaction. For these ions, our
f-values appear to be in general good agreement with the other
theoretical results, again expected to be correct.
For the last several ions
we have used the energies obtained in our MCDF calculations for extracting
quantum defects to be used in RQDO procedure. This has lead to no breackage
in the steadily decreasing trend of the RQDO f-values with increasing
Z, which can be taken as a sign of consistency of the RQDO procedure. One
possible feature that may explain the discrepancies between the RQDO
oscillator strengths and those obtained by Biémont (1986a)
(which are, in no case, greater than 8%) is his reported perturbations
between the
transition with a few theoretical results,
which seem to be the only data available in the literature. For the first
four ions, it is possible to compare our oscillator strengths with data
reported by Biémont, using the same HXR method as in the above transition
(Biémont 1986a), and with the f-values obtained with the
length and velocity forms of the dipole transition operator by Nahar &
Pradham (1993) within the Opacity Project. Their method of
calculation, the close coupling (CC) aproximation using the R-matrix method,
explicitly accounts for configuration interaction. For these ions, our
f-values appear to be in general good agreement with the other
theoretical results, again expected to be correct.
For the last several ions
we have used the energies obtained in our MCDF calculations for extracting
quantum defects to be used in RQDO procedure. This has lead to no breackage
in the steadily decreasing trend of the RQDO f-values with increasing
Z, which can be taken as a sign of consistency of the RQDO procedure. One
possible feature that may explain the discrepancies between the RQDO
oscillator strengths and those obtained by Biémont (1986a)
(which are, in no case, greater than 8%) is his reported perturbations
between the ![]() and
and ![]() configurations, which have a non-negligible influence on the
configurations, which have a non-negligible influence on the ![]() transition probabilities. The mixing
between the
transition probabilities. The mixing
between the ![]() and
and ![]() terms of the
terms of the ![]() configuration, as detected by Biémont (1986a) from his analysis
of the energy data (Corliss & Sugar 1979a, b; Sugar & Corliss
1979, 1980) may also be responsible for the aforementioned
discrepancies.
configuration, as detected by Biémont (1986a) from his analysis
of the energy data (Corliss & Sugar 1979a, b; Sugar & Corliss
1979, 1980) may also be responsible for the aforementioned
discrepancies.
| Z | ION | RQDO | MCDF | Other theoretical values |
| 19 | KVI | 0.1348 | 0.1401 | 0.1384 |
| 20 | CaVII | 0.1258 | 0.1357 | 0.1321 |
| 21 | ScVIII | 0.1180 | 0.1309 | 0.1291 |
| 22 | TiIX | 0.1113 | 0.1262 | 0.1205 |
| 23 | VX | 0.1117 | 0.1217 | |
| 24 | CrXI | 0.1068 | 0.1174 | |
| 25 | MnXII | - | 0.1133 | |
| 26 | FeXIII | 0.0976 | 0.1094 | |
| 27 | CoXIV | 0.0937 | 0.1057 | |
| 28 | NiXV | 0.0911 | 0.1021 | |
| 29 | CuXVI | 0.0860 | 0.0986 | |
| 30 | ZnXVII | 0.0803 | 0.0952 | |
| 31 | GaXVIII | 0.0720 | 0.0919 | |
| 32 | GeXIX | 0.0697 | 0.0888 | |
| 33 | AsXX | 0.0691 | 0.0858 | |
| 34 | SeXXI | 0.0676 | 0.0830 | |
| 35 | BrXXII | 0.0697 | 0.0804 | |
| 36 | KrXXIII | 0.0660 | 0.0781 | |
| 37 | RbXXIV | 0.0523 | 0.0760 | |
| 38 | SrXXV | 0.0478 | 0.0742 | |
| 39 | YXXVI | 0.0436 | 0.0725 | |
| 40 | ZrXXVII | 0.0399 | 0.0711 | |
| 41 | NbXXVIII | 0.0366 | 0.0698 | |
| 42 | MoXXIX | 0.0335 | 0.0688 | |
| 44 | RuXXXI | 0.0288 | 0.0670 | |
| 45 | RhXXXII | 0.0267 | 0.0664 | |
| 46 | PdXXXIII | 0.0249 | 0.0659 | |
| 47 | AgXXXIV | 0.0234 | 0.0654 | |
| 48 | CdXXXV | 0.0220 | 0.0651 | |
| 49 | InXXXVI | 0.0232 | 0.0648 | |
| 50 | SnXXXVII | 0.0179 | 0.0647 | |
| 51 | SbXXXVIII | 0.0190 | 0.0646 | |
| 52 | TeXXXIX | 0.0182 | 0.0645 | |
| 53 | IXL | 0.0175 | 0.0646 | |
| 54 | XeXLI | 0.0165 | 0.0647 |

Figure 1: Oscillator strengths versus the reciprocal of the nuclear charge
for the ![]() transition in the silicon isoelectronic sequence. *: RQDO, this work.
transition in the silicon isoelectronic sequence. *: RQDO, this work.
![]() : MCDF, Huang (1985).
: MCDF, Huang (1985).
![]() : HXR, Biémont (1986a, b)
: HXR, Biémont (1986a, b)
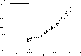
Figure 2: Systematic trends of the oscillator strength of the ![]() transition along the
silicon isoelectronic sequence. *: RQDO, this work.
transition along the
silicon isoelectronic sequence. *: RQDO, this work.
![]() : MCDF, Huang (1985).
: MCDF, Huang (1985).
![]() : HXR, Biémont (1986a, b)
: HXR, Biémont (1986a, b)
In Table 3 (click here) we include only our RQDO f-values given that an extense MCDF
calculation, using Declaux's code (1975), has been reported by Huang
(1985). For the ![]() transition, our RQDO results, which explicitly account for core
polarization effects, are close in magnitude to the HXR f-values reported
by Biémont (1986a, b), by Bromage (1980) and
Bromage et al. (1978), as well as other theoretical values,
which are claimed by their authors to be correct.
However, the MCDF
f-values from Huang (1985) show very large discrepancies
with the rest of the theoretical results displayed in Table 3 (click here).
These discrepancies increase with atomic number, being the MCDF oscillator
strengths too small. When comparing these MCDF data with those of our own
MCDF calculations (not shown in the Table 3 (click here)), the latter present
the same feature roughly the same characteristics as Huang's
(1985). This leads us to suggest that the MCDF procedure is not
adequate for this particular transition, possibly due to cancellation
effects in the transition integral. Biémont (1986b) also
attributes the large discrepancies observed between Huang's f-values and
his HXR f-values to an incorrect assignment of the
transition, our RQDO results, which explicitly account for core
polarization effects, are close in magnitude to the HXR f-values reported
by Biémont (1986a, b), by Bromage (1980) and
Bromage et al. (1978), as well as other theoretical values,
which are claimed by their authors to be correct.
However, the MCDF
f-values from Huang (1985) show very large discrepancies
with the rest of the theoretical results displayed in Table 3 (click here).
These discrepancies increase with atomic number, being the MCDF oscillator
strengths too small. When comparing these MCDF data with those of our own
MCDF calculations (not shown in the Table 3 (click here)), the latter present
the same feature roughly the same characteristics as Huang's
(1985). This leads us to suggest that the MCDF procedure is not
adequate for this particular transition, possibly due to cancellation
effects in the transition integral. Biémont (1986b) also
attributes the large discrepancies observed between Huang's f-values and
his HXR f-values to an incorrect assignment of the ![]() energy levels by Huang (1985).
We once more explain the
much less important discrepancies observed between the RQDO oscillator
strengths and the HXR ones (Biémont 1986a, b) to their explicit
inclusion of configuration mixing. This seems to be particularly important
between
energy levels by Huang (1985).
We once more explain the
much less important discrepancies observed between the RQDO oscillator
strengths and the HXR ones (Biémont 1986a, b) to their explicit
inclusion of configuration mixing. This seems to be particularly important
between ![]() level corresponding to the final
level corresponding to the final ![]() state, and the
state, and the ![]() level and more so as Z
increases (Biémont 1986a), as in the previous transition.
level and more so as Z
increases (Biémont 1986a), as in the previous transition.
For the singlet-singlet ![]() transition, we have calculated oscillator strengths using our semiempirical
procedure RQDO only. In Table 3 (click here) our f-values are compared with other
theoretical results. The most extense calculation is the MCDF one performed
by Huang (1985). This author has accounted for electron
correlation by including all relativistic configurations in the n=3
complex.
transition, we have calculated oscillator strengths using our semiempirical
procedure RQDO only. In Table 3 (click here) our f-values are compared with other
theoretical results. The most extense calculation is the MCDF one performed
by Huang (1985). This author has accounted for electron
correlation by including all relativistic configurations in the n=3
complex.
|
Z | ION | RQDO | MCDF | others | RQDO | MCDF | others | ||
| 19 | KVI | 0.4467 | 0.0762 | 0.6472 | 1.0901 | 1.061 | 1.0024 | ||
| 20 | CaVII | 0.3977 | 0.0826 | 0.5024 | 0.9873 | 0.9549 | 0.8934 | ||
| 0.678/0.674 | |||||||||
| 21 | ScVIII | 0.3850 | 0.0862 | 0.3991 | 0.8956 | 0.8640 | 0.8148 | ||
| 22 | TiIX | 0.3679 | 0.0876 | 0.3319 | 0.8160 | 0.7864 | 0.7431 | ||
| 23 | VX | 0.3480 | 0.0874 | 0.2825 | 0.7385 | 0.7197 | 0.6935 | ||
| 0.266 | 0.744 | ||||||||
| 24 | CrXI | 0.3067 | 0.0861 | 0.2891 | 0.6809 | 0.6617 | 0.6325 | ||
| 25 | MnXII | 0.2948 | 0.0839 | 0.2825 | 0.6297 | 0.6106 | 0.5902 | ||
| 26 | FeXIII | 0.2935 | 0.0810 | 0.2698 | 0.5862 | 0.5652 | 0.5383 | ||
| 0.268 | 0.582 | ||||||||
| 0.2761 | 0.5768 | ||||||||
| 27 | CoXIV | 0.3008 | 0.0775 | 0.2576 | 0.5474 | 0.5244 | 0.5024 | ||
| 28 | NiXV | 0.2692 | 0.0735 | 0.2350 | 0.5143 | 0.4878 | 0.4688 | ||
| 0.20 | 0.51 | ||||||||
| 29 | CuXVI | 0.2375 | 0.0691 | 0.4840 | 0.4547 | ||||
| 30 | ZnXVII | 0.2781 | 0.0644 | 0.4578 | 0.4251 | ||||
| 31 | GaXVIII | 0.2603 | 0.0593 | 0.4398 | 0.3988 | ||||
| 32 | GeXIX | 0.2398 | 0.0540 | 0.4194 | 0.3756 | ||||
| 33 | AsXX | 0.2189 | 0.0462 | 0.3998 | 0.3555 | ||||
| 34 | SeXXI | 0.1991 | 0.0419 | 0.3831 | 0.3382 | ||||
| 35 | BrXXII | 0.1775 | 0.0348 | 0.3654 | 0.3234 | ||||
| 36 | KrXXIII | 0.1635 | 0.0267 | 0.3532 | 0.3109 | ||||
| 37 | RbXXIV | 0.1511 | 0.0175 | 0.3505 | 0.3002 | ||||
| 38 | SrXXV | 0.1362 | 0.0083 | 0.3419 | 0.2912 | ||||
| 39 | YXXVI | 0.1224 | 0.0021 | 0.3340 | 0.2836 | ||||
| 40 | ZrXXVII | 0.1087 | 6.05(-5) | 0.3271 | 0.2770 | ||||
| 41 | NbXXVIII | 0.0956 | 0.0004 | 0.3208 | 0.2713 | ||||
| 42 | MoXXIX | 0.0834 | 0.0016 | 0.3151 | 0.2662 | ||||
| 44 | RuXXXI | 0.0512 | 0.0041 | 0.3115 | 0.2576 | ||||
| 45 | RhXXXII | 0.0428 | 0.0048 | 0.3070 | 0.2537 | ||||
| 46 | PdXXXIII | 0.0349 | 0.0050 | 0.3029 | 0.2501 | ||||
| 47 | AgXXXIV | 0.0274 | 0.0048 | 0.2993 | 0.2466 | ||||
| 48 | CdXXXV | 0.0209 | 0.0041 | 0.2960 | 0.2433 | ||||
| 49 | InXXXVI | 0.0148 | 0.0031 | 0.2931 | 0.2401 | ||||
| 50 | SnXXXVII | 0.0095 | 0.0020 | 0.2905 | 0.2370 | ||||
| 51 | SbXXXVIII | 0.0054 | 0.0011 | 0.2882 | 0.2339 | ||||
| 52 | TeXXXIX | 0.0023 | 4.44(-4) | 0.2863 | 0.2309 | ||||
| 53 | IXL | 0.0004 | 1.15(-4) | 0.2846 | 0.2280 | ||||
| 54 | XeXLI | 0.0000 | 2.24(-6) | 0.2832 | 0.2252 |
Our semiempirical f-values are in better agreement than in previous transitions with the values obtained with the quite much more complex procedures, even with the results obtained using the ample Multiconfigurational Dirac-Fock method, possibly due to the less delicate level perturbation situation here.
Finally, in Figs. 1 (click here) and 2 (click here) we compare the oscillator strengths corresponding to the last two transitions, respectively, in graph form. For that purpose, we have plotted the f-value for the entire group of isoelectronic ions against the reciprocal of the atomic number Z. These figures also serve the purpose of reflecting systematic trends in the individual f-values along the isoelectronic sequence, which have long been considered (Wiese & Weiss 1968) as a qualitative proof of correctness and allows, when they are regular enough, the interpolation or extrapolation of non-calculated data.