5. Automatic classification

We have attempted to classify the 355 LPVs based on three parameters characterizing their mean light curves: period P, amplitude A, and asymmetry factor f. Mennessier (1985) realized such classification on a smaller sample covering a shorter time span of observations. Ludendorff (1928) made an earlier classification of LPVs based on the shape of their visual light curves (see also Mattei 1983).

We used a dynamical clustering, which is a non-hierarchical analysis (Murtagh & Heck 1987), and point out that the optimum number of clusters from the inertia criterion seems to be six. From several random initial conditions the best partition was extracted.

Each cluster of the best partition is characterized by its position in (P, A, f)-space as given in Table 3 (click here). It turns out that P and A are independent parameters in this classification, but that f appears in linear combinations with P and A. The classification is realized in terms of the four variables P, A, 100f-5.9A, and 100f-0.0022P, which are discriminant parameters, and are easily determined from observations.

  
Table 3: The characteristics of the six best clusters as achieved from an automatic classification (dynamical clustering), n is the number of stars belonging to each cluster

5.1. Properties of stars in each cluster

5.1.1. Spectral types

The number of stars of each cluster according to their spectral type is given in Table 4 (click here). It is notable that 80% of C stars belong to cluster C3. Still, this cluster also contains M stars, so this classification is not sufficient to discriminate C-rich from O-rich LPVs. Note the similarity between clusters C2 and C4 (in which there are no carbon stars), as well as that between C3 and C5 (which contain most of the C stars and SRs respectively).

  
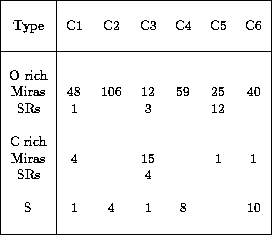
Table 4: Number of stars in each cluster according to different types

5.1.2. Maser emission

The contingency table of maser emissions and our clustering is given in Table 5 (click here). In each column the number of stars is indicated, followed (in parentheses) by 100 times the ratio of the observed frequency to that which is expected if the variables are independent:

where n is the total number of individuals, the total number in line i and the total in column j. Significantly high and low ratios are indicated by one or two underlines respectively.

  
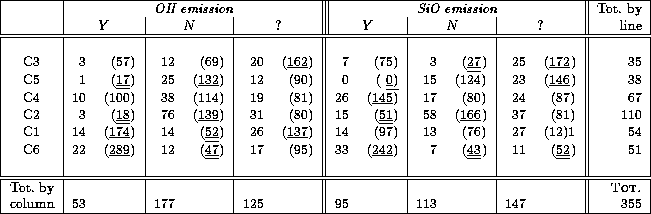
Table 5: Contingency table of our classification and maser emissions. Y and N respectively signify a "yes'' or "no'' to maser detection

As can be predicted, maser emission has not been searched for among C stars. The significant frequencies confirm that:

1. OH emission is related to longer period and asymmetric light-curves (C1 and C6) and not to short-period variables (C2 and C5).
2. SiO emission is related to longer period and large amplitude (C6 and C4) and not with short periods (C2 and C5).

5.1.3. Other classifications

Automatic classifications using the dispersions , , were performed by Brito et al. (1992). The aim of this paper was to check a method of symbolic clustering by comparing it to a classical method. Their results led to a six-cluster classification; the contingency table with ours is given in Table 6 (click here) (the numbers have the same meaning as in Table 5 (click here)). We conclude that:

1. S2 and S6, whose members are characterized by small or mean values of the three dispersions, are related to C3 and C5. This agrees with known properties of SR and C stars.
2. Mean or high values of dispersions (S4, S1, S5, S3) are mainly associated with clusters C1 and C6, which contain the most asymmetric light-curves.

  
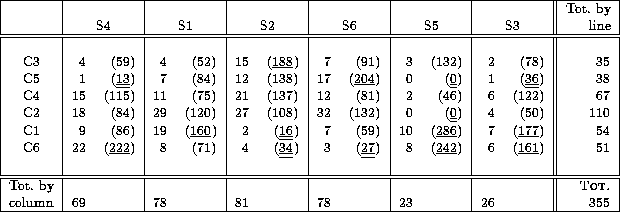
Table 6: Contingency table of our classification and the one obtained from the dispersions of light curve parameters