After the acquisition of the cluster sample our goal was to determine the apparent 
-magnitude
and other fundamental parameters for each of the program galaxies. Unfortunately, the du Pont
film (and plate) was not suitable for this purpose due to the lack of sensitometer marks.
Thus, we decided to do photometry with a first generation glass copy of the Schmidt plate
SRC 323J from the archive of the ESO headquarters in Garching. The plate is
equipped with 7 step sensitometer marks on its northern and eastern margin
allowing to establish the density-to-intensity transformation.
The part of the Schmidt plate 323J which coincides with the surveyed field
was digitized with the Perkin Elmer PDS 1010A 2-D micro-densitometer system
at the ESO headquarters. After the calibration of the instrument with an
unexposed area (plate fog) at the edge of the plate, 16 subfields covering
the survey region were scanned in the density mode with a 12 bit A/D
converter. 25 
m were chosen for the size of the squared beam aperture as
well as for the step size of the scan. With a plate scale of 67.5 arcsecs/mm
and a seeing of 2.3arcsecs for the particular ESO Sky Survey plate, this
led to a slight oversampling. The seeing value was derived from the faintest stars
on the plate. The scanning velocity is inversely correlated to the maximum reliable
density that can be registered by the system. We chose 
20mms
enabling us to measure densities up to D=3.1. This density limit is somewhat
higher than the expected saturation level due to photographic processes at
or 
21.5Barcsecs
. In this way, the dynamical range of
the plate was covered best.
Additionally to the science field the two strips of sensitometer marks were fully traced. In Fig.2 (click here) we show plots of their smoothed profiles averaged over 50 scanning rows. While the northern strip yields very well defined density steps, with the exception of the highest, the average profile of the eastern strip is of only poor quality. Several density steps show gradients superposed by strong defects. No accurate measurements of these density values were possible. This circumstance together with the fact that no log(I)-values were available for the eastern projector, neither in the UKSTU-Handbook (Tritton 1983) nor from the Royal Observatory in Edinburgh, constrained us to work with the northern marks only.
To establish the characteristic curve of the plate we used the bi-logarithmic
formula proposed by Llebaria & Figon (1981):
where 
of the original formula is replaced by the more convenient
quantity I=E/t. The different parameters have the following meaning: I
and D are the relative intensity and the density, respectively.
is the density at which the photographic plate becomes saturated,
is the zero-point density of the photographic emulsion, and C
is the zero point. The analytic curve was 
-fitted at the points defined
by the density values of the northern step marks and their corresponding
log(I)-values (Tritton 1983). As already mentioned above, the
highest step of the northern sensitometer mark was not very well defined.
Consequently, a first fit with this original density value was unsatisfactory,
i.e. the derived value of the fit parameter 
was lower than the highest
scanned density found on the plate. To overcome this problem empirically we
applied a 5% correction to the highest step value from 3.039 to 3.179 in
order to reach the highest plate density. Figure3 (click here) shows the curve which fits
best the finally used data points and in Table3 (click here) we list the best-fitting parameters.
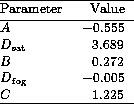
Table 3: Parameters of the characteristic curve
Figure 3: The scanned density values of the northern sensitometer marks versus the
corresponding log(I)-values (plus sign). For the fit of the characteristic curve (line)
we used the values indicated by circles. The highest measured density
had to be slightly corrected for this purpose
For an external quality check of the density-to-intensity transformation
Bender (from the CCD work of Bender 1994) kindly provided us with the major
and minor-axis V-band surface-brightness profiles of the bright
early-type galaxies NGC 4696, 4709, and 4729 in Centaurus.
These profiles were compared with azimuthally averaged profiles in the B-band
we derived for these galaxies (cf. next subsection). As no significant radial colour gradients are
observed for early-type galaxies in general (e.g. Reid et al. 1994),
our profiles should fit between Bender's major and minor-axis profiles after
applying an individual zero-point offset correction. This is illustrated
in Fig.4 (click here). Obviously a good transformation quality is achieved in the
non-saturated regime from 
Barcsec
(
) down
to 
Barcsec
. The accuracy at a fainter level,
between 25.0Barcsec
and 
Barcsec
(which relies mostly on the accuracy of the sky background estimation) can be
judged from the linear shapes of the surface-brightness profiles of
faint dwarfs shown in Fig.5 (click here).
Figure 4: The major and minor-axis surface-brightness profiles in the V-band
for NGC 4969, 4709, and 4729 are shown as lines. Our azimuthally
averaged surface-brightness profiles are added as dotted circles.
The best-fitting offset from the B-band to the V-band magnitude
system was determined individually for each galaxy
Each individual zero-point offset is the sum of the calibration constant of our instrumental
magnitude to the B-magnitude system and the B-V galaxy colour which could
be used to calibrate our magnitude system in principal. But neither 
nor
B-V
are very well known for the three galaxies (Sadler 1984; Poulain 1988;
Dressler
et al. 1991;
Longo & de Vaucouleurs 1983;
de Vaucouleurs et al. 1991; Prugniel et al. 1993).
The neighbourhood of each cluster galaxy image was disentangled interactively from surrounding stars. To do this we used procedures developed in the image processing program MIDAS. If possible, stars projected on a galaxy surface were eliminated by taking advantage of the symmetric property of the galaxy. The pixels of such a star were substituted by the pixels lying on the point symmetrical opposite of the galactic centre. In cases where this technique was not applicable, e.g. the opposite pixels were also contaminated by stars or the galaxy showed asymmetrical appearance, the underlying galactic ground was modelled by fitting locally a second order 2D-polynomial.
After the galaxy image was star subtracted we determined for the galaxy a growth curve based on
a visually selected centre. The pixel intensities were integrated in concentric round apertures
of increasing radius in steps of 1 pixel (=1.68'') outwards. Simultaneously, the sky intensity
was subtracted so the growth curve became asymptotically flat for sufficiently large radii and
a correct sky background determination. This first growth curve was used to define the maximum
radius where all light of the galaxy is included and the noise of the background starts to dominate.
A new galaxy centre was defined by the luminosity-weighted first moment of all pixels within the
maximum aperture and the second (final) growth curve 
was established for the galaxy.
Apart from few cases this growth curve was smooth enough to derive the corresponding instrumental surface-brightness profile:
The profile was approximated analytically in three possible ways depending on
the Hubble type of the galaxy. Classically, the light profiles of ellipticals or the spheroidal
components of disk galaxies were described by the 
-law (de Vaucouleurs 1948).
A more general approach represents the generalized exponential law (Sérsic 1968): 
or 
, where
the exponent remains free instead of being fixed at n=1/4. It has been shown recently
(Caon et al. 1993; Graham et al. 1996) that this formula offers a much better approach
to the observed profiles of elliptical galaxies. We were thus motivated to fit most of
these profiles by this analytic form. The shape parameters n are listed
in the CCC.
S0's and spirals consist of two different profile components. The inner bulge follows the de Vaucouleurs law as the ellipticals. The outer disk part shows a linear decay of the surface brightness corresponding to an exponent n=1 in the generalized exponential law. Consequently we fitted a two-component model at the profiles of these galaxies.
Profiles of some bright nucleated dwarf galaxies (dE, N and dS0, N) exhibit
a clear bipartition. In these cases we approximated the profile by a
two-component exponential model (Binggeli & Cameron 1991). Generally, a classical
exponential law was used for the dE's, dS0's, Im's, and BCD's as well as for some
dE, N's and dS0, N's. Note that the nuclei of dE, N's or dS0, N's in
Centaurus have a
typical size of 
. Therefore, the seeing effect and the discreteness
of the scanning process can easily destroy the central light excess in
the empirical surface-brightness profile.
The innermost radius limit for all fits was 3arcsecs and a lower limit in
instrumental surface-brightness was applied equivalent to 27Barcsec
.
For some bright galaxies the centre of the image was saturated due to photographical
limitation. Here, the fit was restricted to the undisturbed outer part of the profile
starting at an equivalent surface brightness of 21.5Barcsec
.
The model-dependent parameters 
and 
were derived
from the pure exponential outer part of a profile. As the surface brightness
scale is logarithmic, an exponential profile appears as a straight line. The
linear extrapolation of the best-fitting line into the centre yields
the central exponential surface brightness 
. The exponential
scale length 
of the galaxy corresponds to the slope of this line.
Moreover, we determined three model-independent parameters for each galaxy:
the instrumental total magnitude 
, the effective radius 
(radius containing half of the total light), and the mean effective surface
brightness 
. For those galaxies with no saturation
problems in the surface-brightness profile we analysed the observed growth curve
for this purpose. In particular, the asymptotic limit of the growth curve at maximum
aperture defined the total instrumental intensity of the galaxy.
For all other cases, the parameters were derived from the growth curve corresponding
to the best-fitting surface brightness model.
Figure 5: Selected non-smoothed mean surface-brightness profiles in order
of decreasing total apparent magnitudes are shown. The CCC numbers are listed,
along with the galaxy classifications. The points are plotted at 1'' intervals. Notice the
saturation effect in the inner part of the CCC130 profile and its correction
by the best-fitting model
As already mentioned above, there were few galaxies, mainly faint early-type dwarf galaxies, where the growth curve was so badly affected by sky background noise that a derivation of the surface-brightness profile would require to run a smoothing algorithm first. All structure parameters have been derived from the best-fitting model of an integrated pure exponential law into the noisy growth curve starting at r>3'':
with 
, I the intensity, and 
the
exponential scale length.
For illustration we present in Fig.5 (click here) an arbitrarily chosen collection of eight calibrated surface-brightness profiles. In the upper left diagram the saturation effect due to the limits of the photographic plate is clearly visible. A fit of a generalized exponential law to the undisturbed outer part of the profile was used to extrapolate into the central region.
All our magnitudes were corrected for the geometrical vignetting effect of the UKSTU Schmidt telescope. We used the experimentally determined vignetting function (cf. Dawe & Metcalfe 1982; Tritton 1983). In general, the correction factor varies on the photographic plate from 1.0 at the centre to 1.25 at 4 degrees off axis. At the position of the Centaurus cluster on plate 323J a typical correction of 3% had to be applied.
Because of the difficulties to quantify the effect of the desensitization of
hypersensitized plates ("Malin effect''), no correction was applied for
this additional effect. It has been studied in detail by
Campbell (1982) and a maximum error of less than 
is quoted by
Dawe & Metcalfe (1982).
The goal was to transform the instrumental magnitudes
into CCD B-magnitudes. For this purpose
two sets of independent data were used from the literature. A selected
sample of bright galaxies was taken from the Surface Photometry Catalogue of the
ESO-Uppsala Galaxies (Lauberts & Valentijn 1989 hereafter LV). These magnitudes proved to
be in good agreement with the standard RC3 system (Paturel et al. 1994).
The selection criteria we applied to find those galaxies which are most reliable for
the calibration were twofold: First, the central part of the surface-brightness profile
must not be affected by saturation effects. Second, our
derived value for 
should not differ too much from the effective diameter 
given by LV. The
motivation for the second constraint is based on an existing discrepancy
between LV and other authors about the 
values of an early-type
galaxy sample (cf. Fig. 9 in LV). Based on this uncertainty we arbitrarily
fixed the allowed maximum deviation between 
and 2
at 15%.
By this selection we expect to take into consideration only the uncontroversial
galaxy data of both studies. The two constraints were met by 10 galaxies.
LV offers only few galaxies fainter than 
. Thus, we supplemented
the calibrator sample with a CCD-based data set of 22 dwarf galaxies
(Bothun et
al. 1989 hereafter BCS89). This second sample covers well the magnitude interval
and will improve the calibration accuracy at the faint end.
The two data sets of LV and BCS89 galaxies are collected in Table4 (click here).
Figure 6: The upper graph shows the calibration diagram based on 32
selected galaxies in common with LV (circle) and BCS89 (triangle).
The indicated line is not a fit, but a line with unity slope representing
a perfect relation between two magnitude systems. Obviously, this line is
very well approximated by the data points. The residual diagram for our
-magnitudes is given in the bottom panel
Figure 7: 
-magnitudes of all galaxies in common with LV. Filled
circles are
galaxies used for the magnitude calibration. Open circles are galaxies required
individual corrections for central saturation effects
We converted the CCD B-magnitudes from the BCS89 sample to the bandpass
IIIa-J (
) using the colour equation 
as determined by
Metcalfe
et al. (1995). The approximately equivalent relation 
was
applied on the 
-magnitudes of LV. The calibration diagram
is shown in Fig.6 (click here). A
linear fit quantifies the transformation rule to be
. If
restricted to the magnitude range of
particular interest between 
and 21, the fitted line differs at most
from a transformation rule with a unity slope. Based on this good agreement
we assumed an underlying relation 
and determined the zero point
with ZP=-23.23. This value was applied to transform our instrumental magnitudes
into 
-magnitudes. The rms scatter in Fig.6 (click here) is 
which translates
to an uncertainty of the calibration zero point of 
.
Subsequently all 
-magnitudes were converted into B-magnitudes using the colour
equations given above where the measured colours were available. The average colour of
the BCS sample 
was used where colours had not been measured. The
last value is about equivalent to B-R=1.49 and comparable to the mean B-R colour of
for all LV galaxies in common (not only the calibrators).
Figure 8: Comparison of the model- depending parameters 
and
for a sample of early-type dwarfs in common with BCS89. The
solid lines represent perfect agreement between the two data sets
A weakness of photographic plates is the relatively small dynamic range they
cover. Long-time exposures are leading to saturation effects on central parts
of bright galaxies (cf. Fig.4 (click here)). The surface-brightness profile of such a
galaxy had to be extrapolated to the centre in a way as described before. To get an
idea how well this procedure worked, we compare in Fig.7 (click here) the 
-magnitudes
of the 10 uncorrected LV calibrators with those of other 28 galaxies in common with
LV which required a saturation correction. We found good statistical agreement between
the two samples, 
and
with only a slight systematic error for
the corrected sample of 
. This result shows the reliability of
our correction procedure within the expected magnitude error as described below.
Furthermore, we note that the complete LV sample covers a wider colour range
0.8<(B-R)<1.7 than the calibrators. Apparently the transformation rule between the
instrumental and B-magnitude systems seems to work well for all these galaxies.
The photometric accuracy of the instrumental magnitudes was estimated from
the residuals illustrated in the bottom diagram of Fig.7 (click here). First
of all it is satisfactory to see that there are no systematic magnitude
differences between our magnitudes and those of the bright and faint calibrator
samples, respectively: 
and
. We conclude
that the global
errors of our 
-magnitudes for brighter galaxies are comparable
to the typical
uncertainty 
for LV magnitudes (Paturel et al. 1994). We further
propose an error of 
for galaxies fainter than 
.
BCS89 published the model parameters 
and 
for their
22 faint galaxies which can be used to estimate the accuracy of other structure parameters.
In Fig.8 (click here) we plot the scale length and central exponential surface brightness data
of our studies. Obviously, good agreement is found for 
. The
typical error is 
and no systematic offset is evident in
the data. In the case of 
we find a mean difference of 
with a standard deviation of 
.
Most of the dwarf elliptical galaxies exhibit in first order a pure
exponential surface-brightness profile (e.g. Binggeli & Cameron 1991) which
relate
the effective radius and the scale length by the equality
.
Taking advantage of this formula we estimate the error for 
to be roughly the same as that of 
. The error of
may be 
combining the uncertainties of
and 
.
Acknowledgements
This paper is part of the PhD thesis of one of the authors (HJ). He would like to thank his supervisors G.A. Tammann and Bruno Binggeli for their interesting ideas and invaluable advice. We are most grateful to Ralf Bender who made available to us galaxy surface-brightness profiles as well as to the ESO head quarter in Garching for giving access to the PDS plate-scanning machine. We thank Ken Freeman and the referee Dr. E. Bertin for having read the manuscript and having improved the origin version by many suggestions. HJ thanks the Swiss National Science Foundations for financial support.
