4. Estimation of the cluster luminosity function. The initial mass function

4.1. The luminosity function LF

In view of the contamination of field stars for 15.5 mag, we applied a statistical treatment of data to estimate the cluster LF. The method relies upon the removal of field stars in the diagram of Fig. 5 (click here)a. To carry out the procedure a comparison area was measured at from Cr 272 which diagram is shown in Fig. 8 (click here). The lack of a fast routine precluded us to assess the completeness of our photometry; however, star counts per magnitude bins shown in Table 4 (click here) are indicating that in the cluster and the comparison field, the completeness is quite similar. Anyway, we are confident that down to mag (three magnitudes above the detection limit) the completeness should be reasonably acceptable.

  
Figure 7: The vs. diagram. Symbols as in Fig. 4 (click here). The Schmidt-Kaler ZAMS (1982) and the isochrones (Maeder & Meynet 1988) are superposed. Numbers above the isochrones are the log of age. The vertical right axis shows the scale. The cross is indicating the position of star V659 Cen from Fernie et al. (1995) data. Open circles are the brightest stars of the neighbor open cluster Hogg 16 (Vázquez & Feinstein 1991b)

  
Figure 8: The V vs. B-V diagram of field stars

Before removing stars, the comparison field counts were increased by a factor of 4.5 to compensate the different sizes of the areas we measured. Figures 5 (click here)a and 8 (click here) were subdivided into bins of size mag and = 0.25 mag. In particular, the counts per bins of Fig. 8 (click here) were smoothed by means of the product of a marginal distribution and a relative distribution ; in this way, we obtained expected field counts which were then subtracted bin per bin from Fig. 5 (click here)a. With the left counts we constructed the V distribution of statistical cluster members.

   

10-11 3 -

11-12 12 -

12-13 13 3

13-14 28 4

14-15 67 11

15-16 116 27

16-17 186 35

17-18 282 72

18-19 354 80

19-20 127 3

20-21 8 2

21-22 2 -

22-23 1 -

Note: The column containing the counts of field stars is not scaled (see text).

   

11-12 -2.2, -1.2 0.846 0.180 5 1.44

12-13 -1.2, -0.2 0.666 0.180 5 1.44

13-14 -0.2, 0.8 0.502 0.148 15 2.01

14-15 0.8, 1.8 0.362 0.132 16 2.08

15-16 1.8, 2.8 0.239 0.114 45 2.60

16-17 2.8, 3.8 0.135 0.094 39 2.62

17-18 3.8, 4.8 0.047 0.082 33 2.60

Note: The first and second column contain the V and ranges whithin which the counts of Col. 5 were performed. Columns 3 is the log of the stellar mass according to Scalo (1986) and Col. 4 is the mass logarithm difference. Column 6 is the IMF obtained with a least squares fitting where data of the last bin were not taken into account. The parameters of the least squares method, the fitting slope "x", the slope error "Se" and the regression coefficient "R" are given in the bottom of the table.

This distribution is still affected by photometric errors based upon Poisson statistics of counts in a digital aperture which, as shown in Fig. 3 (click here), increase at faint magnitudes, and by photometric uncertainties of the transformation equations and the internal photometric errors (altogether ). After reducing the counts in each bin to the central frequencies we estimated that the influence of all these errors together causes the counts in each bin to be decreased by less than 4% in relation to the original ones. The final impact of these errors on the LF estimate is however negligible when comparing to the Poisson errors of the counts in every bin that were between 10-20 times larger. After all these corrections we obtained the cluster LF shown in Col. 5 of Table 5 (click here).

Is this LF representative of the whole cluster LF? To answer this we used the Digitized Sky Survey plates, DSS, to compute the apparent size of the cluster (shown by the circle in Fig. 1 (click here)) firstly. We started by counting stars in a large area including Cr 272. Taking concentric annuli around a centroid (determined with the bright cluster members) we found that at from it the cluster stellar density merges into the general stellar field density. Thus, we adopted as the cluster size.

Our second step was to re-calibrate the star magnitudes obtained from the DSS plates using a CCD photometric sequence in Cr 272. In this way we produced a set of magnitudes with a detection limit around and typical errors of 0.5 mag. We had to deal, however, with some blended and/or saturated stars uniformly distributed across the plate. Next, the sample was subdivided into two groups shown in Fig. 9 (click here)a: the first one contains all DSS stars found within the cluster boundaries (the circle of Fig. 1 (click here)) while the second is composed by only those stars found in the whole area covered by our survey. If we assume that the cluster members are similarly distributed in the two samples we would not expect to find any significant difference between them. These two samples were then compared by means of a test, which demonstrated that they are the same with more than 90% reliability, at least down to . Therefore, the secures that our estimate of the LF shown in Table 5 (click here), performed in the area covered by our five frames, represents the whole cluster LF.

  
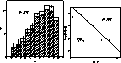
Figure 9: a)  The mag distribution computed with all stars detected in the DSS plate within the circle in Fig. 1 (click here) (clean histogram) and with the stars detected in the zone covered by the five frames (dashed histogram). The vertical scale is logarithmic and the bars are the Poisson errors.   b)   The IMF of Cr 272. The solid line (slope 1.8) is the least squares fitting in which computation the less massive point was not taken into account

4.2. The initial mass function (IMF)

We derived the initial mass function from the cluster LF through a known mass-luminosity relation. To compute the slope of the mass function we performed a least squares fitting using the expression = .

We adopted the mass-luminosity relation found by Scalo (1986), shown in columns two and three of Table 5 (click here); but, previously we compared it to a mass-luminosity relation derived from Schmidt-Kaler (1982) data. We found a reasonable agreement between the latter and Scalo's with typical differences in and, consequently, in of -0.018 and 0.008 respectively when . Any of these two mass-luminosity relations leads therefore to slope-values differing by no more than a few hundredths.

To avoid incompleteness effects in the determination of the IMF slope we just considered the range , this is from V =10 to V= 16.5 mag where we have maximum certainty on statistical memberships and photometric completeness. Table 5 (click here) includes in the last column the value derived from the LF together with the corresponding slope value, x=1.8.

The cluster IMF is graphically shown in Fig. 9 (click here)b. At level, it is steeper than the corresponding to a Salpeter (1955) law with x=1.35 and just at level there is a weak approximation to a Salpeter law. When it is compared to average slopes obtained for groups of open clusters of distinct ages (Tarrab 1982), it is also steeper than the expected for clusters of 13 My (from x=0.3 to x=1.5) and even a bit more than the resulting average slope of "composite" cluster IMFs (). We want to mention that, on the other hand, the slope of the IMF of Cr 272 resembles typical slope-values mainly found in the outer galaxy field (Conti 1992).