Figure 6: a-c) Plots showing how small gain differences in the radiometers
can lead to a bad path correction. a) Propagation delays (in arbitrary units) to two
antennas as a function of time, alternating between the calibrator (C)
and target object (X). The abrupt changes are the result of a
difference in elevation between C and X (C has lower elevation in this
case). Also shown is the difference between these quantities, which is
the required path correction. This also has small discontinuities
(arrowed), since the path correction is different for the lines of
sight to X and C. b) The derived path correction if 
. c) The resulting error in the path
correction. The average error level is removed by phase referencing, but the
steps remain
Any radiometry system, whether it measures fluctuations in the noise level of existing receivers, or consists of separate,
dedicated instruments, measures a signal that is related to the amount
of emission E from the water vapor. This is converted into the path
excess S through a gain factor g, i.e. S = g E. The fluctuations
in the amount of water vapor along a line of sight can be typically of
order a few percent of the total water vapor column (Paper I), so that
the fluctuating part of S is small compared to its absolute value. The latter scales linearly with the airmass and in the Owens Valley,
site of the millimeter array run by Caltech, ranges from 
to
100 mm in the zenith direction.
The path excess derived from a single radiometer is given by 
, where 
is an estimate of the true gain factor: 
. The error 
includes uncertainties associated
with the instrument (gain, bandpass, spillover, etc.), and also
uncertainties in the atmospheric model used to convert emission into
path delay (e.g. temperature profile, altitude of the turbulence).
Ideally, the path excess should be measured to within 
;
when observing at 230 GHz (
), the required accuracy is therefore
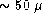m. Since 
can be 
(50 mm zenith delay at 
elevation), it
is necessary that 
for this absolute
measurement.
For an interferometer with radiometers on antennas 1 and 2, the
differential path correction 
is estimated by 
. The calibration requirement in this case is that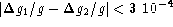 
, i.e. the gain factors have to agree
with each other to within 0.03%. The errors in the gain factors,
and 
, can be substantial, so long as they are
the same for all radiometers. It follows that the uncertainty in the
atmospheric model is largely unimportant for this differential
measurement. However, a small quantity (the difference in the
effective path lengths) is being estimated by subtracting two large
numbers (
and 
) which are measured independently, and the
level of calibration needed is still daunting. These ideas are
illustrated schematically in Fig. 6. The difference signal in Fig. 6a is small compared to the individual measurements, and a small error in the relative calibration of the radiometer gains generates a path correction (Fig. 6b) that is in error by
the amount shown in Fig. 6c.
In practice, this stringent calibration requirement can be relaxed
slightly, since it is only necessary to reference the phase on the
target source X to the phase on the calibrator C, i.e. it is sufficient to measure
the quantity 
as an estimate
of the phase change that water vapor introduces between observations of
the target and calibrator. Phase referencing then removes the error that is
common to both target and calibrator measurements, and only the steps in
Fig. 6c remain.
The difference in the water vapor column between the lines of sight to
the target and the calibrator can still be substantial, however. The
difference in path excess, 
, to an antenna for
sources at elevation 
but separated by a small elevation
offset 
is given by
where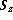 
is the path excess in the zenith direction. The worst case
is for low 
and high 
. For example, for
, 
and 
mm,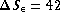 
mm. The requirement is now that the
radiometers must be calibrated to the level of 
with respect to each other, i.e. all
radiometers in the system must give the same value for the path delay from a given column of water vapor to within 0.1%. Two methods that
attempt to achieve this are outlined in Sect. 3.4 (click here).
The value of 
chosen for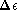 
is typical (in many
cases optimistic) for existing millimeter arrays. Arrays proposed for
the future (e.g. the National Radio Astronomy Observatory Millimeter Array
and the Japanese Large Millimeter and Submillimeter Array) have
substantially higher sensitivity, and therefore have access to a much
larger number of calibrator sources. If 
is
used in the example above, then only 2% precision is required in the
agreement between the radiometers.
The method just described assumes that radiometry is used to correct
the phase changes due to water vapor introduced in moving from the
target to the calibrator and back (the small discontinuities in 
in Fig. 6a), in addition to correcting the
fluctuations during each on-source period. It is the former that
demands tight calibration of the radiometers, and so it is instructive
to investigate the level of phase errors remaining if only the
on-source fluctuations are removed. In this case, the average phase
correction for each on-source period is made equal to zero.
Figure 7 (click here) shows the result of doing this, for a case where
the time 
spent on the target is four times longer than the time
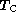spent on the calibrator. The plot is similar to
Fig. 4, except that the radiometry corrects all
fluctuations with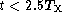 
for the target and 
for
the calibrator. The
residual rms phase for this specific example can be estimated from the
diagram: the uncorrected (aliased) area is approximately 40% of the total for
the calibrator, corresponding to an rms phase error of 
at
230 GHz.
It is also possible to estimate the level of calibration needed for the radiometers in this case.
The rms phase with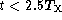 
that is being corrected by the
radiometry while observing the target is 
, i.e. an rms path correction of 
m. Path
corrections of 
mm would not be uncommon, so that an
accuracy of 50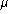 
m requires that 
%.
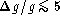By reducing decorrelation and increasing the coherence time of the interferometer, this partial radiometric correction offers a substantial improvement over phase referencing alone. Using radiometry to its full potential, however, requires a method of achieving the much more stringent calibration requirements outlined in 3.2 (click here).
Figure 7: Phase power plots showing the result of correcting on-source
fluctuations only. This example has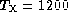 
s and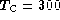 
s. The residual phase error is dominated by the aliased contribution from the calibrator
To ensure that the full radiometric phase correction does not do more
harm than good, all radiometers need to be calibrated to have the same
sensitivity to water vapor to within 1 part in 
(Sect. 3.2 (click here)), i.e. if all the radiometers were to look at the
same column of water vapor (difficult to arrange in practice) then they must give the same reading to
within 0.1%. Although the response of radiometers to hot and cold
loads can be determined to this level of precision, small differences
in the bandpass shapes, spillover, scattering, etc., will inevitably
introduce systematic uncertainties in the response to water vapor. The errors
introduced will be a function of elevation and the prevailing
atmospheric conditions (e.g. temperature profile, altitude of
turbulence), both of which vary with time. There may also be a residual
gain variation of the radiometers themselves that is not removed by a
hot and cold load calibration. The relative calibration of the
radiometers should therefore be made against a column of water vapor on
the sky, frequently enough to follow variations in the response. Two possible
calibration schemes have been identified.
For a given baseline, windspeed and thickness of the turbulent layer,
there is a timescale 
beyond which there is very little
fluctuation power. The data presented in Paper I indicate that for a
100 m baseline, during typical conditions in the Owens Valley, there is
very little power for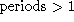 
hour. This timescale is longer for
the 500 m model shown in Fig. 1 (click here), but this does
not include the effects of an outer scale to the turbulence, which will
reduce the power on long timescales.
The radiometer gains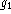 
, 
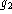, etc., should therefore be scaled to
ensure that the phase corrections derived for each baseline
(Fig. 6b) average to zero, over periods exceeding
(Fig. 2 (click here) for factor of 2.5). This effectively
calibrates out all variations in 
, 
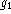, etc. with period
greater than 
. By also monitoring over a long period how the difference between
radiometer measurements on a baseline vary as a function of elevation
and azimuth, the effects of different spillover patterns can also be
reduced.
This method assumes that the antennas are at the same altitude and that the atmosphere can be considered planar over the area of the array. If these conditions are not satisfied, the long term average of the atmospheric phase fluctuations will be non-zero, but it may still be possible to estimate the offsets to the required level of precision. The long averaging times needed for long baselines means that this technique is likely to be more practical for short baselines.
Another possibility is to observe two bright calibrators whose
positions are well known and well separated in elevation (thereby emphasizing the steps in Fig. 6). In the
absence of atmospheric fluctuations the phase measured by an
interferometer should be the same for each source, assuming that each
is at the phase center and that baseline errors are negligible. This
should also be the case after radiometry has been used to correct for
atmospheric fluctuations, and the radiometer gain factors can be scaled
to ensure this. Because of the 
ambiguity in phase, there are
many scalings that satisfy this condition. The correct relative scaling
can be found by measuring several bright calibrators at different
elevations initially, and then subsequently correcting for drifts by
using just two calibrators.
An observing cycle that uses two calibrators (in addition to the target source) has the advantage that while one is used as a phase reference to remove instrumental drifts, the other one can be mapped in parallel with the target, as a useful check on the phase correction and imaging procedure.
This method can be used to remove variations in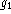 
, 
, etc.,
with periods exceeding twice the observing cycle time. The
disadvantages are that time must be spent observing an object that is
not of direct interest, and the method will not correct errors
introduced by different spillover patterns.
There are several other possibilities that could improve phase correction without the stringent radiometer calibration described above.
The technique of phase self-calibration (e.g. Readhead et al. 1980) can be used to remove
phase errors that are not measured directly. The use of radiometry for
correcting fluctuations during each on-source period means that
self-calibration can be applied to periods of data up to the on-source
time 
. If the instrumental drift is slow, then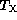 
can be made
large, and it will be possible to self-calibrate on much fainter objects
than was possible without radiometry; radiometry effectively increases the
coherence time of the interferometer.
Another possibility is to filter out the frequencies in the derived
phase correction that result from the error pattern shown in
Fig. 6c, before the correction is applied to the data in post processing.
The power spectrum of this error signal consists of peaks centered on
frequencies of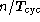 
(where n is a positive integer), widths that depend on the variation in
over time, and strengths proportional to
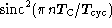. By removing those frequencies
where the error phase power exceeds the atmospheric phase power, the
phase error can be reduced substantially. This technique will be more
successful for shorter baselines where there is less power on long
timescales, and when the gain factors of the radiometers vary only
slowly with time, giving narrower peaks in the error power spectrum. It
is also important that the observations of the target and calibrator
are as regular as possible.
An increase in the array sensitivity through larger antennas, a greater
number of antennas, or more sensitive receivers, for example, allows
fainter calibrators to be used that can be found much closer to the
target. This reduces the size of the steps in 
and 
in
Fig. 6a and therefore reduces the error introduced by
differences in the radiometer gains. The same is true for a site that
has a lower column of water vapor above it. Phase correction using
radiometry will therefore be much easier for the future generation of
millimeter arrays, with many antennas at a drier, high altitude site,
than for the existing arrays.
If an average radiometric path correction is derived and applied to the
incoming signals for contiguous time intervals of duration 
,
then all fluctuations with 
can be corrected. In
the ideal system, the correction would be made in real-time, either by
applying appropriate phase offsets to the local oscillators at each
antenna, or by applying the offsets in the correlator. The limiting
value of 
is then set by the sensitivity of the radiometry
system, and could easily be less than 1 second. This form of correction
is irreversible, however, so that a bad radiometer measurement could do
more harm than good to the astronomical data. Until water vapor
radiometry becomes a reliable technique, it would be prudent to apply
as much of the correction as possible offline. Offline corrections will
also be needed to account for gain changes in the radiometers, as might be determined from the two calibration procedures described above.
At the Owens Valley Millimeter Array, continuum data are recorded every
10 s, so that with a purely offline correction, fluctuations with
s go uncorrected. Reference to Fig. 7 of Paper I
indicates that there is generally little phase power on these
timescales in the Owens Valley, so that an offline correction every
10 s would be adequate in most cases for the continuum data. The much
larger quantity of spectral line data is typically recorded at
intervals of 1 to 5 minutes, however. A purely offline correction is
much less effective in this case, unless the sampling time can be
reduced substantially.
Figure 8: a-d) The effect of residual phase errors on the ability to resolve
a small object. a) Phase power distributions as a function of fluctuation period t for four different
baseline lengths. The hatched region indicates the fluctuations
contributing to the phase error for each integration on the
calibrator. b) Visibility amplitude 
from one integration as a
function of baseline length for an unresolved point source of unit
flux, with (dashed line) and without (solid line) phase fluctuations. The shaded region shows the
distribution of amplitudes that might be expected, scattered about the
average value. c) Amplitude for one integration, corrected for
decorrelation by dividing by the corresponding calibrator amplitude.
d) The amplitude expected after vector averaging over many
integrations, with radiometry used to correct the decorrelation in each
integration