The usual observing procedure for millimeter arrays is to interleave
observations of the target object with a point-like calibrator. This is
known as phase referencing. An observing cycle usually consists of
several integrations of duration 
on the target, followed by a
single integration on the calibrator. For example, there might be four
5-minute integrations on the target followed by a 5-minute integration
on the calibrator, giving a cycle time 
of 25 minutes. The
amplitude and phase measured on each baseline for the calibrator change
with time, as a result of instrumental drifts and atmospheric
fluctuations. A complex gain curve is fitted to the calibrator
observations as a function of time, and is then removed from the
measurements of the target object.
The next two sections quantify how phase fluctuations get folded into this observing procedure. Some contribute to a decorrelation (i.e. reduction in the visibility amplitude) within each integration, some are effectively removed, while others result in phase errors in the complex visibility measurements.
The complex visibility sampled by an interferometer can be written as
where the 
is the visibility
intrinsic to the brightness distribution on the sky, and 
is the variation in the phase introduced by the atmosphere and
instrumental drifts. Variations in the amplitude gain have been ignored.
After integrating for time 
, the averaged visibility is
described by 
, where f (
) reflects a reduction in the amplitude through decorrelation, and 
is a phase error.
Rapid fluctuations tend to get averaged out and
contribute little to 
but dominate in f; conversely, fluctuations with
periods much longer than 
have very little effect on f and a large impact on 
. It
can be shown (see Appendix) that the total phase power remaining after
averaging the fluctuations over 
is given by
where 
is the spectral density of the phase fluctuations at the output of the correlator (units: rad
Hz
).
Figure 2 (click here) shows
the sinc
function plotted on a logarithmic horizontal scale, and
how it is well approximated by a step function that becomes zero for
. The rest of the phase power goes into the decorrelation of the measured amplitude:
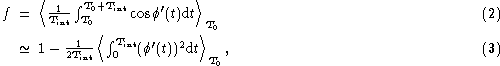
where 
represents the phase fluctuations with period
, the angled brackets denote an ensemble average over all values of 
, and the approximation is valid for 
. The second integral gives the power of 
, and can be expressed as an integral over the relevant frequencies of the power spectrum, so that
Changing the variable of integration from 
to 
gives
which shows that the area of the distribution in Fig. 1 (click here) with
is a measure of the decorrelation, 1-f.
Figure 2: 
is well approximated by a step function with the
transition at 
The visibility amplitudes measured for the calibrator also exhibit decorrelation, which can be quantified as a function of time for each baseline and then used to correct the corresponding amplitudes on the target object. Although this restores the average amplitude to the correct level, the amount of decorrelation is somewhat random from one integration to the next, and the uncertainty in the corrected amplitude is increased (see Figs. 8 (click here)a and b). Note also that decorrelation is fundamentally a baseline-based quantity and cannot be expressed as a combination of antenna-based contributions in the same way that is possible for phase errors.
The phase measured on the target for a given baseline is referenced to the corresponding phase measured on the calibrator, a technique that eliminates most slow drifts in the instrumental response. The calibrator is chosen to be both bright enough to give sufficient signal-to-noise in a single integration, and as close to the target as possible to reduce position-dependent errors (e.g. from uncertainty in the relative locations of the antennas).
The cycling time between observations of the calibrator is 
.
This sampling rate can follow any component of 
(the phase variation remaining after integration) with a period longer
than the Nyquist limit of 
. These fluctuations constitute
the true "slow" component. A slow component fitted to the calibrator phases
will not represent the true slow component, since there are errors
introduced to each calibrator measurement by a "fast" component, comprising those
fluctuations with a frequency exceeding the Nyquist limit. This is
illustrated in Fig. 3 (click here). The error caused by the fast
component (shaded) looks like a slow component. This is the result of
aliasing. The error component is white phase noise up to a
high frequency cut-off of 
.
Figure 3: Illustration of how phase fluctuations from the fast component
(
) cause an error in the fitting of the slow
component (
). The fast component is effectively
aliased into a slow error component
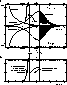
Figure 4: a) Phase power plot showing the contributions from
the atmosphere and the instrument (schematic only). The upper and lower
halves represent the calibrator and target measurements, respectively.
The phase variance in the diagonally hatched region causes
decorrelation of the amplitudes measured in time 
. Phase
fluctuations in the "bricked" zone are correlated between the
target and calibrator and are removed by phase referencing. The residual
phase fluctuation power in the target observations after phase
referencing comprises equal contributions from the target and the calibrator (blank regions in lower and upper halves, respectively).
b) Spectrum of the residual phase errors. The contribution from the calibrator is actually aliased to lower frequencies, so that it has a white noise spectrum up to a cut-off frequency of
(the sharp distribution is a result of the
logarithmic horizontal scale)
The fitted slow component is subtracted from the phases measured on the
target object as a function of time. This removes the effects of all
phase fluctuations with a period longer than 
, but leaves
the phase fluctuations from the target and calibrator for which 
, as
illustrated in Fig. 4a. After phase referencing, there remain equal contributions to the phase error from the target and calibrator measurements. Since the calibrator contribution is aliased to lower frequencies, the spectrum of the phase errors has the appearance depicted in Fig. 4b.
The specific example shown in Fig. 4 uses the atmospheric model of Fig. 1 and
has 
s
and 
s. For an observing frequency of 230 GHz, the phase
variance from fluctuations with 
on each of the target
and the calibrator is 
, corresponding to 
50%
decorrelation. The total phase error 
is 
, consisting of equal contributions from the calibrator (the
aliased component) and target measurements.
One method for reducing the aliased component is to increase the shortest
period 
of the
curve fitted to the calibrator phases (Fig. 3 (click here)), so that it
becomes over-sampled and no longer passes through all of the
measurements. Only fluctuations with period 
are
removed, so that the blank area in Fig. 4a corresponding to the uncorrected component is increased. Careful consideration of the effect of over-sampling, however, shows that the area of the aliased component on the calibrator is reduced by a factor 
, which can potentially more than offset the original increase.
The optimum choice of 
, 
and 
depends on the phase power distribution (which depends in turn on the
baseline length and orientation, windspeed, thickness of the turbulent
layer, etc.) as well as instrumental constraints. Two cases are
discussed briefly.
When 
is of order 1000 s, the spatial offset between the
target and calibrator is unimportant for the cancellation of
atmospheric fluctuations; the calibrator might as well be coincident
with the target, as long as the elevation is not too low. This point is illustrated in Fig. 5 (click here). The
wavelength of any fluctuation that is part of the slow component is
much larger than the separation 
of the lines of sight to target and calibrator as they pass
through the turbulent layer. It is then sufficient to subtract the
fitted phase as a function of time on the calibrator from the measured
target phases without worrying about the time offset 
, so that for the slow component of the phase error, 
.
Phase referencing becomes less effective at low elevations. There are two
reasons for this: 
becomes larger, and, more significantly,
the amplitude of large-scale phase fluctuations is proportional to
the airmass 
. Although fluctuations with
are correlated between target and calibrator, they are
stronger for the object at lower elevation. The fractional error in
the phase referencing correction is 
, where 
is the average of the two elevations and 
is the difference.
Another important point is that the impact of phase fluctuations does not increase indefinitely as the baseline gets longer. This is discussed further in Sect. 4 (click here).
Figure 5: A water vapor fluctuation (part of the slow component) at
average height 
with wavelength 
. The
distance between the lines of sight to the target (X) and calibrator
(C) at height 
is 
. For w=5 m s
, 
s,
, 
and 
km,
values of 
km and 
km are obtained
In principle, 
(and therefore also 
and 
)
can be reduced to timescales of order 10 s, below which there is very
little phase fluctuation power. In this regime, the separation of the lines
of sight to the target and calibrator, 
, is comparable to the
wavelength of the smallest fluctuation that can be sampled,
. For such fluctuations, it is no longer a good
approximation to say that 
; instead, a time lag
needs to be introduced: 
, where in the
one-dimensional case 
. The two-dimensional reality
requires that 
and w are treated as vectors, with 
. There is then a residual, uncorrected
phase error associated with the separation of the target and calibrator
perpendicular to the wind direction.
The time overhead associated with rapid switching between sources is generally prohibitive for existing arrays - calibrators can be over 
from the target and the antennas are not designed to be agile - but fast
phase calibration is being seriously considered for future arrays (e.g. Holdaway 1992; Holdaway & Owen 1995).