A solution lies in taking the one-dimensional scan to pieces in
a Fourier analysis. Fourier theory (e.g. Bracewell 1965)
indicates that any continuous function
may be represented as the sum of sines and cosines, i.e.
where the function F representing the phased amplitudes of the
sinusoidal components of f is known as the Fourier Transform (FT).
If the function is sampled N times at uniform intervals
in the spatial (observed) frame, the total length in the
t- direction is 
, and
the result is
the continuous function multiplied by the ``comb" function,
producing a function f'(t) which (with the interval in
spatial frequency as 
)
may be represented (e.g. Gaskill 1978)
either as a sum of sines and cosines
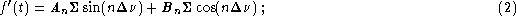
or as a cosine series
where amplitudes 
and phases 
are given by
In the latter formulation, obtaining the FT
produces - by virtue of the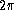 
cyclic nature of sine and cosine -
a ``Fourier-Transform plane" for
f'(t) which shows the amplitudes
mirror-imaged about zero frequency, with a sampling in spatial frequency
at intervals of
and a repetition of the pattern at intervals
of 
.
There are three criteria for successful discrete-sampling.
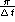. (Consider
the silly case of a signal which is a spatial sine wave of
wavelength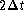 
: sampling at
intervals of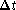 
finds points of
identical amplitude and thus does not carry information on amplitude or
phase of this spatial frequency.) Thus the sampling interval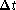 
sets
the highest spatial frequency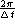 
which can be present;
if higher frequencies are present in the data, this sampling rate
loses them.
At the same time, the sampling theorem
(Whittaker 1915; Shannon 1949) indicates that any
bandwidth-limited function can be specified exactly by regularly-sampled
values provided that the sample interval does not exceed a critical length
(which corresponds approximately to half the FWHM resolution),
i.e. if the instrumental half-width is B,
if 
.
to be effectively zero. If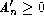 
for components of frequency this high,
the positive high-frequency tail of the repeating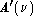 
tangles up with the negative tail of the symmetric function
repeating about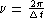 
to produce an
indeterminate transform.
. Such
low-frequency spatial components may be real
as in the case of a stellar spectrum, or
may be instrumental in origin as for sky scans with a single-beam radio
telescope. In either case, to have any chance of distinguishing these
from those of the signal, the scan length must exceed the width
of single resolved features by a factor preferably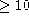 
.
In practice most data satisfy these properties. By design, sampling is
frequent enough to maintain resolution, to obtain spatial frequencies beyond
those present in signal, and to avoid aliasing. By design we take
spectra over ranges substantially greater than the width of the
features. Consider for instance the FT of the spectra in the upper panels
of Figs. 1 (click here) and 2 (click here), whose 
are shown
in upper panels of Fig. 3 (click here) and Fig. 4 (click here). Only half the
interval of the FT is shown in these plots,
up to 
; the amplitude of the components
has drained away very satisfactorily.
It is therefore appropriate to consider what can be done to
such scans via harmonic analysis, filtering in the Fourier (frequency)
plane, and reconstruction.
Figure 3:
Upper panel: The amplitudes of the Fourier components of the spectrum in
Fig. 1, top. Central panel: The amplitudes of the Fourier components of the
patched spectrum (with the least-squares approximation subtracted) of
Fig. 1, middle. Note the change in scale, due to the removal of the
massive low-frequency signal present in the lines.
Lower panel: The same amplitude plane
after application of a half-Gaussian taper of scale 
channels. This is the set of amplitudes used in the reverse FT
which produces the baseline shown in Fig. 1, lower panel
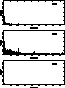
Figure 4:
The FT amplitudes of the complete scan (upper panel), the patched
scan (central panel), and the filtered result from which the baseline is
constructed (lower panel), as described in the caption for Fig. 3
To fit a continuum or remove a baseline, one could in principle consider an optimum filter for removing the prevalent low-frequency components. The difficulty is the well-known property for the FT of a Gaussian to be a Gaussian in the Fourier plane; even unresolved lines thus have very low frequency components. The result is that the harmonic components which govern the baseline are also required for the signal. Indeed simply building a baseline by reverse-transforming the few lowest-frequency components from the transform of the spectrum will produce baselines with gross distortion in regions of signal due to the low-frequency signal components.
However, it is straightforward to ``patch out" regions of signal, as shown in the central panels of Figs. 1 (click here) and 2 (click here). A simple linear interpolation across suspect or manifestly ``bad" (line) regions is easily selected and for the purpose interactive graphics can be used. Such a process is remarkably stable against the choice of the extent of the patches, except for extreme curvature of the baseline.
The next step is to take the FT of this ``patched" array, and then to filter the low-frequency components from this. A formal method can be used, such as the filtering described by Martin (1959); but a simple and effective approach is to apply a savage half-Gaussian taper to the amplitude plane. (Any filter applied needs a taper to prevent ringing effects.) Finally the continuum is reconstructed with the inverse transform of the patched/filtered data.
The FT (amplitude) of the patched arrays are shown in the central
panels of Figs. 3 (click here) and 4 (click here).
The heavy half-Gaussian filter applied
in this instance has a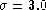 
wave-numbers. The lower panels of
Figs. 3 (click here) and 4 (click here) show
the savagery of the filtering which, when the inverse
transform is applied, yields the highly satisfactory
continua in the lower panels of Figs. 1 (click here) and 2 (click here).
The cyclic nature of the FT technique always means that the ends of the scan must match, so that an overall slope must be removed at the outset. A simple least-squares fitting technique, or very heavy smoothing to estimate a zero-order approximation to the continuum, can be used for this purpose, as shown in the central panels of Figs. 1 (click here) and 2 (click here).
To summarize, the baseline-finding technique advocated here consists of