We employed the standard LTE line analysis program WIDTH6 of R.L. Kurucz adapted by V. Tsymbal for using on IBM PC. Atmospheric models for G-K giants were interpolated within the grid of models given by Bell et al. (1976) and by Kurucz (1979) for dwarfs. For some high luminosity cool stars additional atmospheric models were computed in 1992 by I. Bikmaev using the MARCS code of Gustafsson et al. (1975). The metallicity nearest to the derived iron group abundance was used to derive the final model used for a program star.
Figure 3: The spectra of four program stars along with Procyon near CI 6587.62
Å. Measured features include NiI 6586.31 Å, CI 6587.62 Å, FeI 6591.31 Å,
FeI 6592.92 Å, and FeI 6593.88 Å
The theoretical equivalent width of each line is computed assuming at start the
solar abundance, and the abundance is modified iteratively until the
equivalent width matches the observed one. We determined a giant's
abundances relative to normal G8 giant 
and a dwarf's
abundances relative to Procyon (F5IV-V). For differential abundances
the standard notation 
is used.
There 
, n(x) is the number density of an
element x, and m= the number of lines used. Because the goal of
this study was to identify also mild barium stars, which possess
small s-process overabundances, accurate abundances were required,
therefore, a particular care was taken to ensure a consistency in
the determination of the atmospheric parameters and abundances.
Since the analysis is a differential one, and abundances are
measured relative to those of a similar star, the effects of
systematic errors in the height of the continuum, possible line
blanketing effects in red giants, uncertainties in quantities of the
oscillator strengths, and non-LTE effects are lessened. In order to
improve the accuracy of adopted atmospheric parameters, excitation
temperature, spectroscopic gravity, and microturbulent velocity were
derived using differential abundances of each line relative to the
corresponding line in the standard star instead of absolute
abundances for all iron group elements. We have found that this
improvement led to a high degree of internal consistency in the
analysis. Therefore, we expect that a large number of lines for
stars, great homogeneity of data, and the improvements of the
analysis will ensure a high internal accuracy of the atmospheric
parameters and chemical composition.
Figure 4: a) and b) The comparison of equivalent-widths between
this paper and others for standard stars: a) 
, b)
Procyon
The atomic oscillator strengths were taken from Luck & Bond (1985), Thevenin (1989, 1990), and Gurtovenko & Kostyk (1989) and will be given separately together with the measured equivalent widths. Since the analysis is done differentially with respect to a standard, accurate oscillator strengths are not so critical.
Effective temperatures, 
, were estimated from the
colors using the calibration by Bell & Gustafsson (1989) for giants
and calibration by Bikmaev (1992) for dwarfs. Photometric colors
were taken from the literature. We used the (R-I) broad-band
Johnson system colors taken from the Yale Bright Star Catalogue
(Hoffleit 1982) for giants. These near-infrared colors are
unaffected by the possible violet opacity in peculiar red giant
stars. (B-V) colors were used for most dwarfs. We used the line
excitation equilibrium for the iron group metal lines as an
additional check for temperature determination. To cancel the
possible non-LTE effects, especially for lines of low excitation
potential, we used the differential abundance relative to the
standard. The relation between differential abundances for lines of
the iron group elements and excitation potential is illustrated in
Fig. 5 (click here) for two giants and one dwarf. As can be seen a large number
of lines and a small scatter ensured the low internal errors for our
excitation temperatures and reflect a good quality for the data. We
compared (Table 2 (click here)) our spectroscopic temperatures (
)
with those that can be deduced from colors (R-I) or (B-V). The
agreement between spectroscopic and photometric temperatures is good
for all of the program stars, excluding HD 130255, for which the
excitation temperature is much higher (
) than the
color temperature. In this case we adopted the excitation
temperature also for 
because it is more consistent
with the spectral class. On the whole, the effective temperatures
can be determined to 
.
Table 2: The colours, effective temperatures derived from the colour indices,
excitation temperatures, and the final adopted atmospheric parameters for all
program stars. The last column indicate the averaged abundances of s-process
elements scaled to the metallicities
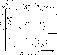
Figure 5: The differential abundances of FeI (
), FeII (+), TiI
(
), TiII (
), CrI (
), and CrII (
)
versus excitation potential relation for three program stars
illustrating the estimation of the spectroscopic temperatures
Gravities 
, were derived requiring both ionized and neutral iron group
element lines to yield the same abundance. It should be kept in mind that
spectroscopic gravities may be affected by departures from LTE when we use
XI/XII ionization equilibrium for the determination, therefore, we used the
differential abundance relative to the standard again. The error in 
as
determined from iron group lines is approximately 
, when g is
measured in 
.
We have derived microturbulent velocities, 
, in the conventional way
of adjusting 
, to eliminate any trend of elemental
abundance with equivalent width. The differential elemental
abundances relative to standard, derived from individual lines of
iron group elements, were computed for a range of 
values. Plots of abundance as a function of equivalent width for
all choices of microturbulence, showed where the dependence
vanished. Typical examples illustrating the 
determination for three stars are illustrated in Fig. 6 (click here). The
microturbulent velocities can be determined to 
.
Figure 6: The differential abundance versus equivalent width relation for
three program stars illustrating the estimation of the microturbulent
velocity. Signs indicate: (
) FeI, (+) FeII, (
) TiI,
(
) TiII, (
) CrI, (
) CrII
The analysis of uncertainties in the derived abundances due to errors in the
model parameters shows that a combination of uncertainties in effective
temperature of 150 K, of 0.3 in surface gravity, and of 
in
microtrubulent velocity would lead to errors no more than 0.2 dex in the derived
abundances for most elements. Since we used existing models for metal abundances
closest (
) to those of the real metallicities there could be
errors due to the model's approximation. We examined errors in the derived
abundances due to uncertainties in model metal abundance [A] of 
. We concluded that these uncertainties lead to errors in the abundance for
most elements no more than 0.1 dex. Since we used the abundances of s-process
elements (barium) normalized to the metallicities (XII) the influence of the
model's approximation to the final results is even less (
). The
independence of wavelength of the differential chemical abundances estimated
from different lines of neutral iron, illustrated in Fig. 7 (click here) for three program
stars, shows that we correctly defined the continuum.
Figure 7: The differential abundance of iron [FeI] versus wavelength
relation for three program stars illustrating a correctly defined continuum