This category includes the late A, the F and the early G stars. We did not
explore the cooler stars although Kurucz models now exist for them, because
their calibration is a delicate matter and was already explored by
Grenon
(1978, 1982) and Grenon & Golay (1979). The philosophy of
the present calibration is roughly the same as in KN90: it uses the d vs.
B2-V1 and the 
vs. B2-V1 diagrams, which are sensitive to effective
temperature, surface gravity and metallicity.
The B2-V1 index is mainly sensitive to 
, while the
reddening-free parameter d is sensitive to both 
and log
.
The new Kurucz models seem more realistic than the previous ones in the sense
that the synthetic B2-V1 indices computed from them are closer to the
observed values.
Figure 9: Inverted and corrected grid log
vs. 
for the
intermediate stars having [M/H] = -1.0. The iso-pT and iso-pG lines
are the vertical and horizontal lines respectively
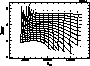
Figure 10: Same as Fig. 9, but for [M/H] = 0.0, i.e. solar metallicity
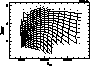
Figure 11: Same as Fig. 9, but for [M/H] = +1.0. Notice that the metallicity
effects are non-negligible at the low-
end of the grid
In the d vs. B2-V1 diagram, however, there was a conspicuous change in slope
of the iso-log
lines for 
at high
gravity and 
at log
.
This change in slope seems to be linked with the onset of convection in the
superficial layers of the star's envelope, and was especially conspicuous in
the 
vs. b-y diagram of Strömgren's photometry (see e.g. Kurucz
1991). Since then, a conceptual error has been detected in the ATLAS9 code
by Dr. F. Castelli (1996). The changes in slope occur when the
convective flux is zero at the last depth in the model because the convection zone
is wholely contained in the atmosphere. The program computed convection
differently depending on whether the last value was zero or not. The program has
now been changed to be consistent and the change in slope has been greatly reduced
or removed. Kurucz has recomputed the convective models and fluxes and will
distribute them on CD-ROMs (Kurucz 1996a, b). We have computed new
Strömgren and Geneva colours (the new Geneva colours were kindly computed
for us by Dr. David Bersier). Figure 14 (click here) shows a comparison between the new grid
(full lines) and the ``old'' one (i.e. before the change to ATLAS9, dotted
lines) in the d vs. B2-V1 diagram for solar metallicity:
there is a significant difference, the new grid looking much smoother.
The grids represented in this figure have not been corrected to match any
standard star. Although the differences involve essentially the cool stars,
the ``intermediate'' grids are also concerned in the vicinity of their
cool edge, i.e. for 
up to 8750 K. Therefore
the intermediate grids have also been recomputed.
Now, although the problem of the slope discontinuity of the iso-log
lines
has been solved in the models, yet another problem remains in the observed
main sequence of the Hyades. The same grid for the new models is represented
in Fig. 15 (click here) together with the observed main sequence of the Hyades cluster:
one clearly sees a sudden change of slope in the observed sequence around
B2-V1 = 0.16 or 
K, which is not reproduced by
the models. This feature is not seen only in the Hyades, since it is present
also in the Praesepe cluster. It had not been noticed by KN90, because these
authors used only the Pleiades cluster, where the scatter is larger.
Though the internal structure models foresee a very small and
gradual decrease of log
with increasing mass and decreasing
on the isochrone, they are quite unable to account for
the sharp decrease around 7000 K the observed sequence would imply if the
atmosphere models were entirely realistic. Therefore, something is missing
in the atmosphere models.
Figure 12: Difference between the photometric and fundamental effective
temperatures for the intermediate stars (assumed to have solar metallicities).
The solid line is the mean and the broken lines define the rms scatter
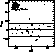
Figure 13: Difference between the photometric and fundamental log
values
for the intermediate stars (assumed to have solar metallicities).
The solid line is the mean and the broken lines define the rms scatter
The standard stars with known 
are listed in Table 9 (click here) with their
sources. They are taken essentially from Blackwell & Lynas-Gray (1994), who
relied on the infrared flux method. We did not use temperature estimates based
on spectrophotometry, since they generally use a fit to the same Kurucz models
and are therefore not fundamental nor independent from our photometric approach.
The difference between the interpolated 
and the fundamental one
is shown in Fig. 16 (click here). The interpolation was done taking luminosity
effects into account, using log
estimates
essentially from the previous version of our calibration, i.e. from KN90. The
conspicuous gap seen between 
and 7900 K is that of
Böhm-Vitense (1970), corresponding to the onset of convection (see
also Mendoza 1956; Böhm-Vitense & Canterna 1974;
Jasniewicz 1984). Since this gap represents a kind of physical
discontinuity, we have fitted two different functions to either side of it: a
horizontal straight line for the hot side (and the gap itself), and a regression
line for the cool side. The correction in 
takes the form:
Figure 17 (click here) compares the fundamental and photometric values of 
.
The rms scatter of the differences amounts to 54 K. The
scatter induced by photometric errors is negligible in comparaison with errors in the fondamental data. The contribution are respectively
7% and 93%.
The standard stars with known log
are listed in Tables 10 (click here) and 11 (click here), and
belong to the Hyades and IC 2391 open clusters respectively. Their log
values have been determined from the models of Schaller et al.
(1992) assuming ages log
for the Hyades and log
for IC
2391. The needed effective temperature was estimated from the previous calibration
of KN90; the interstellar reddening was considered negligible for the Hyades,
while a marginally significant colour excess E(B2-V1) = 0.005 (North &
Cramer 1981) was assumed for IC 2391. In Tables 10 (click here) and 11 (click here), the last two
columns give the log
values and their uncertainty respectively, obtained from
the grids corrected by Eqs. (14-15) above, not from the uncorrected grids.
This holds for all tables where standard stars are listed, for all three
physical quantities 
, log
and [M/H].
The difference 
between the interpolated and fundamental
values is represented in Fig. 18 (click here)a for the Hyades and IC 2391 clusters, as a
function of 
, the corrected effective temperature. A dip about
0.3 dex deep is clearly visible at 
,
which reflects the change of slope of the observed sequence mentioned above.
Since the members of the Hyades cluster draw an iso-metallicity line in the
vs. 
diagram (except for the Am stars of
course), it is not possible to explore the possible effects of metallicity
with these stars alone. Using other old clusters is of little help because
their range in metallicity is small. Therefore, we used the numerous field F
and G stars studied spectroscopically by Edvardsson et al. (1993,
hereafter EAGLNT93), which span about 1.2 dex in [Fe/H] and have empirical surface
gravities derived from Strömgren photometry. Even if their log
values
are not fundamental stricto sensu,
they are much better than nothing as shown in Figs. 18 (click here)b, c and d.
In Fig. 18 (click here)b, where only the stars of EAGLNT93 with 
are
shown together with those of the Hyades, one sees that the field stars of
EAGLNT93 are very well superposed on the Hyades, which tends to validate
a posteriori the surface gravities given by EAGLNT93. In Figs. 18 (click here)c
and d are represented the EAGLNT93 stars with 
, and 
: clearly, the correction
is very much dependent on metallicity for these cool stars.
Fortunately, the metallicity dependence becomes vanishingly small at high
effective temperatures (i.e. 
K), so that the correction
of log
can be safely defined by the cluster stars in that range of
.
Figure 14: Comparison between the models before (dotted lines) and after
the correction (solid lines) proposed by Castelli (1996). Notice the much
smoother iso-log
lines. These grids are the original ones, i.e. they
have not been corrected to fit any standard star
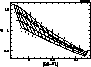
Figure 15: Comparison between the models after the correction, and the
observed main sequence of the Hyades cluster. Notice how the observed
sequence crosses the line log
near 
K.
The grid is not corrected to fit any standard star
The correction is not very simple, and we had to fit several different
functions of the type:
where 
stands for the interpolated and corrected effective
temperature. The coefficients a, b and c are listed in Table 12 (click here).
For 
K, we fitted a straight line rather than
a parabola, so that the c coefficient is identical with zero there.
Strictly speaking, this correction is valid only in the case of
unevolved stars. The surface gravity of F giants will not be estimated
correctly with this calibration. We made many different attempts to extend
the validity of our calibration to giants, using e.g. very old clusters or
well-classified field F giants, but none proved satisfactory. The present calibration in terms of log
must then be
considered as being limited to unevolved, or only very slightly evolved stars.
As a rule of thumb, we may say that it is valid for log 
. The
comparison between the interpolated and fundamental values is shown in Fig. 19 (click here). The rms scatter of the differences is 
dex. But the
scatter is larger for the cool stars than for the hotter ones, because the
iso-log
lines come closer together as 
diminishes. The
stronger dependence on metallicity effects for cool stars probably also contributes to the larger 
.
Figure 16: Difference between interpolated and fundamental 
values vs. fundamental 
for the cool stars.
Notice the gap of Böhm-Vitense between 7400 and 7900 K. The correction is
fitted by a horizontal line at high 
and across the gap,
and by a regression line at low 
.
See Table 9 for the key to symbols
Figure 17: Difference between photometric and fundamental 
values vs. B2-V1 for the cool stars. The solid line is the mean and the
broken lines define the rms scatter. See Table 9 for the key to symbols
Figure 18: a) Difference between interpolated and fundamental log
values vs. photometric 
for the Hyades. Notice the conspicuous
dip at 
K. b) Same as a), but for
field stars of EAGLNT93 having [M/H] > 0.1 (triangles), for the hotter
Hyades stars (full dots) and for members of the young cluster IC 2391 (crosses).
c) Same as b), but for field stars of EAGLNT93 having
-0.1 < [M/H] < +0.1. d) Same as b), but for field stars of
EAGLNT93 having -0.5 < [M/H] < -0.3. Notice the very strong metallicity
effect
Figure 19: Difference between the photometric and fundamental values of
log
vs. B2-V1 for the cool stars. The solid line is the mean and the
broken lines define the average rms scatter. Notice the larger scatter at
large B2-V1. In the key to symbols, ``Ed'' stands for ``Edvardsson et al.
(1993)''
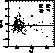
Figure 20: Difference between the photometric (i.e. interpolated and corrected
by Eq. (16)) and fundamental values of [M/H] vs. photometric [M/H], for
stars with 
K. Notice the remaining trend
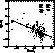
Figure 21: Difference between the interpolated and fundamental [M/H]
vs. photometric 
. The regression line corresponding to Eq. (16)
is shown. The key to the symbols is explained in Table 14; ``Ed'' stands for
``Edvardsson et al. (1993)''
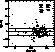
Figure 22: Difference between the photometric and fundamental [M/H] vs.
B2-V1 for the cool stars. The symbols are the same as in Fig. 18.
The solid line represents the mean while the broken lines define the
rms scatter
As in KN90, the metallicity is determined using the 
vs. B2-V1 diagram.
Fortunately, the recent Kurucz models are much more realistic in this diagram
than were the preceding ones. In Fig. 10 (click here) of KN90, one sees how the grid of
iso-
and of iso-[M/H] lines folds again as [M/H] increases
from +0.5 to +1.0; at the same time, 
varies strongly as
[M/H] increases (at given B2-V1). Such complicated behaviour induced severe
problems for the grid inversion as well as in the final 2-d interpolation of the
physical quantities, even though KN90 dropped the most perturbing points.
Furthermore, it was impossible to obtain straightforward estimates of the
physical parameters of Am stars. On the contrary, the new models show no more
folding, i.e. the iso-
curves now have a monotonous behaviour
and they are, furthermore, remarkably straight.
The standard stars used have been taken essentially from the huge
work of EAGLNT93, which contains homogeneous,
high-resolution spectroscopic results for
189 F and G stars. 157 of these stars have been measured in
the Geneva photometric system, which allows an excellent calibration of our
diagram in terms of [Fe/H] (we consider here [Fe/H] to be equivalent to
[M/H], although it is not quite true for very metal-deficient stars). These
standard stars are listed in Table 13 (click here). Some other, hotter objects taken from
other sources (Perrin et al. 1977; Cayrel de Strobel et al. 1992 and
especially Burkhart & Coupry 1989)
are listed in Table 14 (click here). To correct the grid, we had to use a more complicated
method than that of KN90. We first defined a preliminary correction 
as a function of 
(the interpolated and corrected
), which is the only step KN90 had done. A plot of 
vs 
does not show any trend, only a zero point-shift
where the subscript 0 refers to this zeroth-order correction,
while 
is the temperature obtained by interpolation in the
grids corrected by Eq. (14). This correction is shown in Fig. 21 (click here).
In a second step, we plotted the residual 
against the spectroscopic values [Fe/H]: there is a clear trend, as shown
in Fig. 20 (click here). This trend varies slightly with effective temperature,
according to the relation:
where 
is the interpolated metallicity, corrected by
Eq. (17) above; this relation was found using a least-squares fit.
Therefore the difference 
is not so much a function of B2-V1
or temperature, but chiefly
of metallicity [M/H] itself. The latter dependence had been
overlooked by KN90, essentially because of the much smaller number of standard
stars they used. This correction allows us to obtain
a photometric metallicity of the Hyades cluster which agrees well with the
accepted spectroscopic value: we obtain [M/H] = +0.08, while Cayrel et al.
(1985) give 
for the same stars.
It is now possible to treat Am and other metallic stars like any other stars:
for the typical Am star 63 Tau = HR 1376, we obtain
K, log 
and 
. The effective
temperature we find is in excellent agreement with
the value 
K estimated by Smalley
(1993a), who uses the infrared flux method and corrects for the presence
of a cool companion. The surface gravity agrees perfectly with that obtained by
Smalley (1993b) from the 
colours (log g = 4.13). Our
metallicity is a bit smaller than, but still agrees well with that of
Smalley (1993b) who found 
. Notice that
he adopted 
K, which seems too high, and lowering
would imply a lower [M/H] as well. On the other hand,
Burkhart & Coupry (1989) found [Fe/H] = +0.4 on the basis of
high-resolution spectroscopy, in very good agreement with our estimate.
The difference between our photometric [M/H] and the fundamental [Fe/H]
values is shown in Fig. 22 (click here). The average rms scatter of the differences
amounts to 
, which is similar to, though slightly larger
than the scatter found by EAGLNT93 (their Eqs. (13-15)) for the
differences between their [Fe/H] values and the [M/H] values derived from
photometry. When only the stars studied by EAGLNT93 are
considered, our rms scatter drops to a value quite similar to theirs.
Therefore the capability of the Geneva system to estimate metallicities is
excellent; in this regard, this system is quite competitive with the
one.
The inverted and corrected grids are shown in Figs. 23 (click here) and 24 (click here). Figure 23 (click here)
is a log
vs. 
diagram, showing the solar-metallicity grid
with lines of iso-B2-V1 and iso-d parameters. Figure 24 (click here) is a [M/H] vs.
diagram for log
, showing the iso-B2-V1 and
iso-
lines.
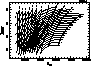
Figure 23: log
vs. 
diagram for the cool stars with solar
metallicity, showing the inverted and corrected grids with iso-d and
iso-B2-V1 lines. B2-V1 varies here between -0.125 and +0.475 and d
between 0.5 and 2.0. Notice the tightening of the lines around
K, which reflects the change in slope of
the observed Hyades' sequence
Figure 24: [M/H] vs. 
diagram for the cool stars with
log
, showing the inverted and corrected grids with iso-
and
iso-B2-V1 lines. B2-V1 varies between -0.05 to +0.50 by steps of
0.05 magnitudes. 
varies between -0.18 to -0.58 by steps of 0.04
magnitudes