Energy levels for Ba I lines have been taken from
Moore (1971). Roig & Tondello (1975) have been studied the spectrum of Ba II in
absorption, by
flash pyrolysis. They found a general agreement with previous results
obtained in emission spectra (see the critical compilation of Moore
1971) but fifteen new levels have been established as well. For Ba II
lines, energy levels were taken from Moore (1971), but values for
8-12p
P
, 10f
F
and
11f
F
, have been taken from Roig & Tondello (1975). Oscillator strengths have been
calculated by using the method of Bates 
Damgaard (1949) and
the tables of Oertel 
Shomo (1968). For higher levels, the
method described by Van Regemorter et al. (1979) has been used.
2
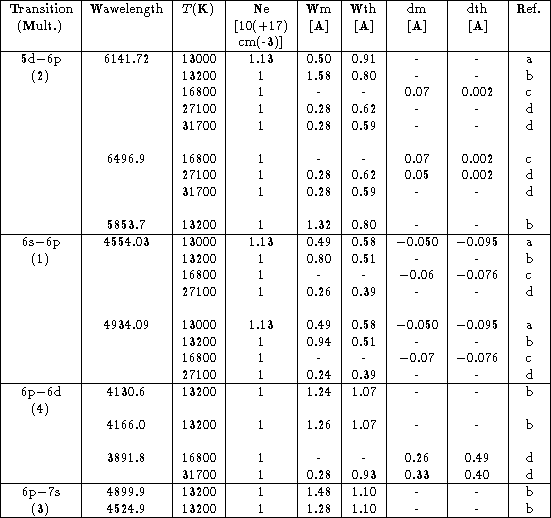
Table: Experimental Stark full widths at half maximum (Wm)
and shifts (dm) in Å
compared with
theory. The Wth and dth are present semi - classical calculations.
Experimental values: (a) - Fleurier et al. (1977);
(b) - Jaeger (1969);
(c) - Puric & Konjevic (1972); (d) -
Hadziomerspahic et al.
(1973)
In addition to electron-impact full halfwidths and
shifts, Stark-broadening parameters due to proton-, and
He II- impacts have been calculated. Our results for 14
Ba I multiplets and 64 Ba II multiplets are shown in
Tables 1 and 2 (accessibles only in electronic form) respectively,
for perturber densities 10
- 10
cm
and temperatures 
K for Ba I and 
K for Ba II. We also specify a
parameter c (Dimitrijevic & Sahal-Bréchot
1984), which
gives an estimate for the maximum perturber density for which
the line may be treated as isolated when it is divided by the
corresponding full width at half maximum. For
each value given in Table 1, the collision
volume (V) multiplied by the perturber density (N) is much
less than one and the impact approximation is valid
(Sahal-Bréchot 1969a,b). Values for
NV > 0.5 are not given and values for 
are denoted by an asterisk. Tabulated Stark
broadening parameters are linear with perturber density
for perturber densities lower than 
cm
.
When the impact approximation is not valid,
the ion broadening contribution may be
estimated by using the quasistatic approach
(Sahal-Bréchot 1991; Griem
1974). In the region between, where
neither of these two approximations is valid, a unified
type theory should be used. For example in Barnard et
al. (1974), a simple analytical
formula for such a case is given. The accuracy of the results obtained decreases when broadening by ion interactions becomes important.
In Table 3 (click here) our results are compared with the experimental results
(Jaeger 1969; Puric & Konjevic 1972;
Hadziomerspahic et al.
1973; Fleurier et al. 1977) critically selected by Konjevic &
Roberts (1976); Konjevic & Wiese (1976, 1990)
and Konjevic et al.
(1984a,b). One can see that large differences between particular
experiments and between theory and experiment exist. An agreement
exists between widths of Fleurier et al. (1977), whose experiment was
critically estimated by Konjevic et al. (1984b) to have the highest
accuracy among Ba II experimental data, and our results for
6s
S - 6p
P
multiplet. For the shift, the best agreement is with the
results of Puric & Konjevic (1972) for the same multiplet.
Our results for Stark width are in agreement with the semiclassical calculations
of Cooper & Oertel (1967) as well as with the
semiclassical calculations by using
the theoretical approach developed by Griem et al. (1962) and further
improved and described in detail by Jones et al. (1971) and Griem
(1974), performed by W.W. Jones (private
communication in Konjevic & Wiese 1976), and Puric et al. (1978).
Our Stark width calculation are also in agreement within the error bars
of the methods with various semiempirical calculations (Hadziomerspahic et al. 1973; Fleurier et al. 1977; Dimitrijevic
& Konjevic 1981) as well as with simple Stark width estimates of
Lakicevic (1983), on the basis of the Stark broadening parameter
dependence on
the ionization potential from the lower level of the corresponding
transition. For Ba I
6s
S - 6p
P
Lakicevic
(1983) obtained FWHM 
Å
at an electron density of 
= 10
cm
and
electron
temperature T=20000 K, and our result is 0.30 Å. For Ba II
6s
S - 6p
P
multiplet for the same plasma conditions, Lakicevic
obtains FWHM 
Å and our result is 0.43 Å.
Our results for the shift are in agreement within the error of the method with the semiclassical calculations of W.W. Jones (private communication in Konjevic & Wiese 1976), but in strong disagreement with calculations of Gorchakov & Demkin (1978), performed within the semiclassical approach of Vainshtein & Sobel'man (1959), with the semi the empirical calculations of Puric & Konjevic (1972) and with the simple estimates of Lakicevic (1983). New high precision measurements of Stark broadening parameters for Ba I and Ba II lines will be of interest for the development of theoretical methods for heavy atoms and ions.
Acknowledgements
This work is a part of the project ``Astrometrical, Astrodynamical and Astrophysical Investigations", supported by Ministry of Science and Technology of Serbia.