Figure 1: Example lightcurve of 97 Klotho with data from the 1992 apparition. The magnitudes are measured relative to the fitted HG phase curve
As a by-product of the phase curve fitting described above we obtain the residual rotational variation. The resulting lightcurves, obtained by folding the data with the assumed or determined rotation period, show a clear signal only if the amplitude is quite high. Note that this method will not work well if changes of the synodic period causes phase shifts during the apparition that are a significant fraction of a rotation cycle. In addition, the problem associated with the strange sampling of the present data must be stressed.
We obtain the best lightcurves for the long-period asteroids (34) Circe and (97) Klotho (see Fig. 1 (click here)). We also tried to calculate a period for (570) Kyhthera from the Carlsberg data, but we obtained no unique results.
![]()
Figure 1: Example lightcurve of 97 Klotho with data from the 1992 apparition.
The magnitudes are measured relative to the fitted HG phase curve
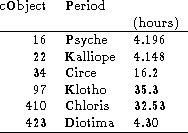
Table 1: Estimated rotation periods

Figure 2: Four example phase curves illustrating a variation of sampling
frequency and scatter in the magnitude measurements.
Note that 27 Euterpe seems to have a linear phase curve
and 28 Bellona may have a steep opposition spike.
However, the data is not really good enough for that kind of
detailed analysis
The period estimations of the lightcurve give fitting errors of only a few percent. This may be misleading in cases where aspect changes cause the synodic period to vary. However, the known periods for (16) Psyche, (22) Kalliope, (410) Chloris and (423) Diotima produced the best lightcurves after Fourier- fitting to the known periods. If the other periods from the Fourier-fit were chosen it was not possible to produce any kind of lightcurve. Most of the periods from the Fourier-fitting are thus artifacts of the sparse data points, and thus the only reliable indicator of the goodness of fitting is the goodness of the produced lightcurve. The estimated rotation periods are presented in Table 1 (click here).