The reduction method which is developped in the following is based on an analytic expression of the fringe packet by means of a Fourier analysis. It does not rely on any model and is thus valid for any geometry of the source. The first part of this section is dedicated to the definition, the calculus and the computation of the phase function. In the second part the problem of reduction is addressed.
Figure 4: Algorithm for the correction of the piston effect
Figure 5: Sequence of functions computed to resample the
interferograms with an opd corrected of the piston effect as defined
by the algotihm of Fig. 4 (click here)
The modulated part of the interferogram as defined by Eq. (6) can be written
as the product of a slowly varying positive function, the envelope, by a rapidly
oscillating function:
where 
is the phase function. 
can be defined in different ways as
it is the argument of a cosine function. For the purpose of the correction
algorithm it will be a monotonic, strictly increasing function. It is not
continuous and makes jumps of 
when the envelope becomes zero and has no
derivative.
The interferogram of Sect. 2 was defined in wide band but is band limited as
the light is filtered. For 
, a wavenumber within the support of the
one-sided spectrum or the spectrum defined for positive wavenumbers, I define the
shifted spectrum S by:
The complex spectrum is now expressed with the shifted spectrum:
This yields a new expression for Eq. (6):
where 
is the Fourier transform operator. Let us now consider the
inverse Fourier transforms of the hermitian and anti-hermitian parts of the
shifted spectrum, noted respectively E and O, and defined as:
leading to a new expression for the interferogram:
O(x) and E(x) are both functions with real values and are odd and even
respectively when the shifted spectrum is real. The expressions of the envelope and
the phase function are straightforward:
The phase function can be mathematically defined as long as the
envelope does not become zero. The problem of properly unwrapping this function
will be adressed in the next section. An interesting property can be derived
from Eq. (16): the interfringe is constant in the interferogram as long as
the O function is a constant and is 0, which is equivalent to saying that the
shifted spectrum is an even function. The expression of the phase function does
not depend on the choice of the wavenumber 
. This property will be
used in Sect. 4.2 and is demonstrated in the appendix at the end of the paper.
As defined by Eq. (16), the phase function is not continous as the 
function is not continuous and returns values in the interval
. The phase is first unwrapped to eliminate
discontinuities larger than 
. The function that is obtained is globally
strictly increasing. Some discontinuities still remain that are not due to the
function. They occur at each zero of the envelope when its first
dervative is not defined. The mathematical function then makes jumps of 
or
. In reality these jumps are not resolved when working with finitely sampled
interferograms. It is not possible to eliminate them: a pistoned phase function
can reproduce a positive unresolved leap. But a negative unresolved leap-like
variation cannot be due to piston as variations induced by piston are supposed to
be smaller than variations of the nominal opd. To insure the final phase
function to be monotonic, the negative leaps are rectified. Numerically, when
the negative leap has been detected, 
is added to the phase function after
the leap, the leap itself is transformed into a positive leap by a symmetry with
respect to the tangent before the leap. The error made on the phase function
after the symmetry is negligeable because the phase function is very close to a
straight line when it is continuous (the interfringe is almost constant). After
these transformations, the computed phase function is monotonic but is defined
with a random additive constant proportional to 
. The value of this constant
is fixed this way: the value of the phase function must be in 
around
the white light fringe.
The piston signal 
is a noise on the variable x, the opd. The idea
to correct pistoned inteferograms is to reduce noise on the opd as statistical
data reductions are usually processed. The main difficulty is to express the opd
as a function of something, that is to say to invert Eq. (16) or part of
this equation. To do this it is necessary to find a one-to-one function of opd.
This function is the computed phase function which will be thereafter mixed up
with the mathematical one, although they are quite different as explained in
Sect. 4.1.3. Let us note 
the p realization of a piston
sequence. The corresponding interferogram, envelope and phase function are
indexed with p. From the unicity property of the phase function and the
envelope, the expression of the pistoned interferogram is:
with:
is invertible as 
is strictly increasing and so is a
one-to-one function. The opd as a function of the phase function can be defined and
is noted 
. The reduced opd function 
is the
average of the realizations of the pistoned opd functions. For an infinite number
of realizations the reduced opd function converges to the nominal opd function.
For N realizations of the piston the residual piston in the reduced
interferogram is thus reduced by a factor 
, the reduced inteferogram
being eventually:
For sake of clarity the correction algorithm is summarized in Fig. 4
and the functions used in the reduction process are plotted in
Fig. 5. Let us
assume that N interferograms have been recorded: 
, each of length 
corresponding to a fixed nominal
opd window width 
or spectral resolution 
with 
. The sampling frequency is at least twice the higher spectral
frequency to obey the sampling theorem.
Let us consider the two-sided spectrum obtained by discrete Fourier transforming
the interferogram. The frequency samples are
where
is the Nyquist frequency. 
is
extracted from positive frequencies, 
from negative
frequencies and conjugated. The sum and the difference of the two are computed.
and 
long zero sequences are added before and after the two
lists to produce the 
and 
functions of Sect. 4.1.2 with 
(half the Nyquist
frequency). After inverse Fourier transform of these two, the phase function is
computed as explained in Sect. 4.1.3.
The previous step yields N pistoned phase functions. They are all defined in
the same temporal window (corresponding to an opd window width 
) but they
do not vary in the same range as the piston randomly shifts the interferograms
position in the window. For each realization i of the phase function, the maximum
and minimum 
of the function are computed. The
common range of variation of all the phase functions is determined to be:
, where
and
. This is the maximum common range
on which opd functions 
can be defined. The phase functions are
linearly interpolated on
producing a sampled opd
function 
for each
interferogram i (the index 
means that the opd function definition
is relative to the phase function whereas the sampled inteferograms
are defined for the set of nominal opds
). The error
introduced by the linear interpolation process is very negligeable because the
pistoned phase functions have variations between two sampling opds that are linear
with a very good approximation as long as the sampling frequency is chosen far
greater than the first cut-off frequency of piston.
The opd functions are then reduced by processing:
yielding an estimation of the opd fluctuations for each interferogram:
The reduced set of opds width 
is smaller than the nominal width
which means the spectral resolution has been decreased by the
reduction process.
The result of the three previous steps is the estimation of the opd as a function
of the nominal opd: 
. The reduced interferograms
or unpistoned interferograms are the following sets of samples:
where the 
are interpolated from the samples
. These sequences are then interpolated to yield regularly
sampled interferograms.
The correction algorithm that has just been presented is used to reduce simulated
pistoned interferograms. The source has a 
K blackbody spectrum and it is
seen through a K filter. It is unresolved with a constant visibility modulus of
one and with a constant visibility equal to zero. Most of the energy is in the
range 
to 
cm
. The number of samples is 1024 and the
parameters are those listed in Table 1. The length of the sequences and the
spectral resolution are the same as in Sect. 3.6. 100 interferograms have been
simulated. Figure 6 shows the result of the reduction. The left view of Fig. 6
is the corrected interferogram. The spectrum of the corrected interferogram
(full line), the original spectrum (square dots), and the spectrum of the pistoned
interferogram (dashed line) are on the right view. In Fig. 7 are plotted one
of the simulated piston sequences (dashed line) and the approximation of the error
signal (full line) as a result of the reduction process. See Sect. 5 for
comments.
Figure 6: Corrected interferogram and spectrum for an infinite S/N. Top view:
corrected interferogram. Bottom view: spectrum of the corrected interferogram
(full line), original spectrum (open circles)
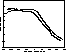
Figure 7: A simulated piston sequence (dashed line) and the error
signal output by the reduction program (full line)
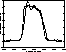
Figure 8: Spectrum after reduction and summation of 100 interferograms with
S/N=100 (the dashed curve is the original spectrum)
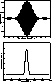
Figure 9: Simulated interferogram in a narrow K band and spectrum
Figure 10: Spectra of interferograms reduced with the narrow band method for three
different S/N ratios. Top view: S/N=100. Middle view: S/N=50. Bottom view:
S/N=20. (The dashed curve is the original spectrum)
The expression of the interferogram given in Eq. (2) requires to assume that
the intensity in the two arms does not fluctuate.
This situation prevails when using single mode
fibers (Coudé du Foresto & Ridgway 1991; Coudé du Foresto et al.
1992)
because all coherent photons injected in fibers do interfer and
because fibers allow to momitor the fluctuations of photometry in the
two arms. The
photometric fluctuations are corrected during data reduction and interferograms
are renormalized.
These variations are low frequency variations
(usually of the order of 
Hz) and the interferograms can be scanned at higher
frequencies allowing for a correct filtering to remove these
variations if fiber optics are not used. Yet, the visivility transfer
function is allowed to vary with time as long as the variations are
achromatic. This then only changes the amount of modulated energy but
it does not change the phase function. In other words, Eq. (2) can be
supposed reliable for the correction algorithm.
The correction simulation of the previous section was carried out assuming an
infinite signal-to-noise ratio. The S/N ratio is defined as in Brault
(1985):
assuming a white noise with rms fluctuations 
in the temporal
domain, the S/N ratio is the ratio of the white fringe amplitude and
: 
. The local S/N ratio is thus
rapidly decreasing in the interferogram with distance to the white light fringe.
For the spectrum simulated in this paper, the S/N ratio at the top of the
first side lobes is only 
of the Brault signal-to-noise ratio. Figure 8
shows the modulus of the spectrum after correction of 100 interferograms with
S/N=100. After correction of piston, spectra have been averaged to reduce the
additive noise. The spectrum correction quality is very degraded
because the phase function computed for a local S/N ratio less than 1 is not
reliable. Besides, the phase function is very sensitive in the zones where the
envelope of the interferogram is zero. As a matter of fact the sign of the
interferogram can randomly change there producing random 
phase shifts. The
more random phase shifts the more different phase functions from one interferogram
to the other. Although the main lobe is corrected with a good quality, additive
noise is a disaster to correct other lobes when the S/N ratio is not very high,
hence the great difference between the corrected spectrum and the original
brightness density. Nevertheless, the correction can be improved. The
interferometer has two outputs which are theoretically complementary because the
input energy is conserved. The detection of the complementary interferogram can be
done differently to use it as a correction interferogram. The use of a narrower K
filter for the second output will increase the coherence length of the beams, thus
widening the envelope of the second interferogram, and will take the first side
lobes away, the first lobe width being proportionnal to the inverse of the
spectrum width. Assuming the amount of noise is the same in the two arms of the
interferometer, the S/N ratio for the narrow filter interferogram is the S/N ratio
times the ratio of collected energy through the K and narrow K filters. The
spectrum seen through the narrow K filter with a 
cm
spectral
resolution is shown in Fig. 9. The S/N ratio for the narrow band interferogram
is approximately degraded by a factor of 5 with respect to the S/N ratio for the
regular K filter interferogram. Series of 100 simulated pistoned interferograms
have been corrected and averaged for S/N ratios of 100, 50 and 20. The resulting
spectra are presented in Fig. 10.
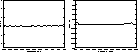
Figure 11: Visibility modulus (left view) and visibility phase (right view) for
an infinite S/N ratio
It is to be noticed that if filters of adjustable width are available
then it is possible to adapt the width of the narrow filter to
optimize the final spectral resolution. As a matter of fact, for large
S/N ratios in wide band the width of the narrow band can be
chosen so that the S/N ratio of the narrow band signal is for example
20 (or larger). The width of the narrow filter is then 
times smaller than that of the wide filter and the resolution of the
wide band spectrum is increased by the same factor. If the method is
systematically applied then the final resolution is inversely
proportional to the S/N ratio of the wide band signal.
The reduction algorithm has to be adapted when a common origin independent of the interferograms is not known with a precision better than one tenth of a wavelength. A common origin is required for all interferograms to define the position functions. It is very convenient to set the position where the phase function is zero as the origin because it can be very accurately determined. The same algorithm can then be applied, the only difference being that the visibility phase is determined to within a constant and does not allow image reconstruction. Accurate phase recovery will be adressed in another paper.
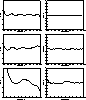
Figure 12: Visibility moduli (left views) and phases (right views) for S/N of:
100 (top views), 50 (middle views) and 20 (bottom views)
The correction algorithm of Sect. 4.2.2 has led to the irregularly sampled
interferograms of Formula (22). The derivation of spectral information from these
sequences is not straightforward. The usual way is to interpolate the irregularly
sampled sequences at regularly spaced opds to get regular samples and compute
their discrete Fourier transform. The interpolating process introduces an extra
noise all the more important as the sampling frequency is lower. This numerical
noise can be reduced by oversampling the original sequences to get better
estimates when interpolating. The corrected low resolution spectra presented in
this paper were obtained using this method. The method fails when high resolution
information is mandatory. Oversampling would increase the number of samples
without increasing resolution, and very long sequences cannot be oversampled
indefinitely. Besides, the residual noise would destroy part of the high
resolution information. A method overcoming interpolation drawbacks is necessary.
An algorithm has been developped by Feichtinger et al. (1994)
to compute spectra from non-uniform samples. The algorithm is iterative and thus
slower than the Fast Fourier Transform algorithm. 25 iterations, which
is roughly 
floating point operations, are needed to
reconstruct the spectrum from 2300 samples with a high accuracy (the normalized
error is less than 
). The time required by the restoration algorithm
increases with the size of the gaps in the samples. The number of iterations would
thus increase with the strength of piston.