This section is dedicated to the characterisitics of piston. The features are used in paragraph 3.6 to simulate piston and pistoned interferograms.
Figure 1: Differential piston power spectrum
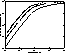
Figure 2: Effective standard deviation of piston for temporal
sequencies of finite length. The standard deviation is normalized to unity for
a sequence of infinite duration. Curves are plotted for three different wind
speeds: 10m s
(full line), 20m s
(dashed line) and 30m s
(dashed and dotted line)
, fried parameter
and baselength D. Its expression in meters is:
refers to the opd fluctuation standard deviation.
It is interesting to realize the importance of this effect. Assuming
correct seeing conditions for observing with 
cm at 2.2
m and
that the interferometer baseline is 
m, the standard deviation for opd
fluctuations is 
that is about 9 fringes in the K photometric band
(to be compared to the coherence length of 10 fringes) and an error of 56 radians
on visibility phase measurements.
Since 
is proportionnal to 
, 
does not depend on
wavelength and piston is an achromatic effect. The reduction method proposed in
this paper mainly relies on this critical property of atmospheric differential
piston.
Let us now focus on the evolution of differential piston with time. A theoretical
average spectrum is given in Conan et al. (1992) for an infinite outer
scale. It is a three-slope spectrum in Log-Log representation with cut-off frequencies
depending on the average speed of turbulent layers v as defined in Roddier
(1981),
also depending on the baselength D and the diameter of the pupils d. These
frequencies have the following expressions:
and the slopes are typical of a Kolmogorov turbulence: 
, 
and
. Considering parameters given in Colavita et al. (1987) for
observations carried out at the Mark III interferometer with a 
m baselength,
a 
m s
average wind speed and 
cm apertures, cut-off
frequencies are 0.6 and 
Hz which is in good agreement with the piston
power spectra published in this paper (the data are in the range 
Hz
and do not display the third slope feature).
The idealized temporal and statistical properties given before are correct to a certain
extent. They require the outer scale of turbulence (scale at which turbulent
energy is introduced in the atmosphere) to be infinite. The relation in Eq.
(7) saturates for baselines larger than the outer scale and energy in the power
spectrum saturates at low frequencies. Recent measurements of the outer scale at
the SUSI interferometer site in Australia (Davis et al. 1995) for
baselines ranging between 5 and 
m state values of about a few meters.
Piston measurements show that relation (7) departs from linearity in Log-Log
coordinates (Fig. 3 of that paper) - for the 
m baseline, the measured
piston standard deviation is 
m whereas the expected value is in the range
m, depending on seeing conditions - and power spectra level out for
frequencies below 
Hz. Although there is a controversy about the
outer scale (references can be found in Davis et al.) it turns out that a finite
range is more likely than an infinite one and that methods based on predictions
from the power spectrum at low frequency that found an infinite outer scale are
not reliable because they are consistant with a wide range of results. Direct
measurements with different baselines are definitely likely to be a good basis
for a good understanding of the properties of piston. As a consequence, the power
spectrum used in this paper, taking into account a finite outer scale, is a
four slope spectrum in a Log-Log diagram with a low cut-off freqeuncy at 
Hz
and the two cut-off frequencies predicted by Conan et al. (1992). It is plotted
in Fig. 1.
Prediction of piston standard deviation by Roddier (1981) applies to sequences of
infinite duration. In real life, interferometric scans are finite in length and,
since piston speed is not infinite, standard deviation on a finite length is
necessarily lower than the prediction. For a sequence of duration T frequencies
below 
are atttenuated thus decreasing standard deviation. In
Appendix A the analytical expression of standard deviation is given as a function
of scan duration. The result is plotted in Fig. 2 for observing parameters
given in Table 1 for three wind speeds (10, 20 and 
) spread
across the range of observed speeds in good astronomical sites (E. Gendron,
private communication). Standard deviation for infinite sequence lengths is
normalized to unity. With 
and for durations in the range 
s
standard deviation is proportionnal to 
whereas it is
proportionnal to 
for shorter durations. In short, attenuation of
piston variations becomes important for sequences shorter than
.
It is interesting to derive the coherence time of piston to get a rough estimate
of the time scale necessary for a piston peak-to-peak variation. In the same
conditions as those used above, the coherence time is found to be:
which means that piston varies slowly and that it has to be determined on long
sequences to be averaged out.
Both piston amplitude and temporal behavior are well known thus allowing
realistic simulations as will be shown in the next section.
Interferometer sensitivity to piston is wavelength dependent. The shorter the
wavelength, the higher the fringe frequency for a given fringe speed, hence the
higher the effective piston coherence time. But, as far as piston amplitude is
concerned, the shorter the wavelength the higher the relative amplitude of optical
path fluctuations. It is of a great interest to know whether a numerical piston
correction
method is more efficient improving amplitude or time coherence. Let us consider
sinusoidal optical path fluctuations as in Brault (1985) of frequency 
and
amplitude 
. In the spectral domain, these fluctuations produce two
symmetric replicas of the spectrum shifted by 
and 
and of
relative height 
. This simple example shows that it is more profitable to
reduce piston amplitude to achieve spectrum restoration as the noise introduced by
piston is proportionnal to its amplitude. It also demonstrates that infrared
wavelengths are more suitable for DFI than visible wavelengths.
The simulations presented in this paper are in the K photometric
band centered at 
m. The simulated interferometer is the fibered
recombination unit FLUOR at the focus of the IOTA interferometer as explained
in Perrin et al. (1995). The characteristics of the inteferometer are listed
in Table 1. The source is supposed to be unresolved at any wavelength in the
band yielding a constant visibility of 1. The spectrum is a spectrum of a
blackbody at 
K seen through a K filter.
Table 1: Simulation parameters
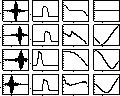
Figure 3: Simulations of interferometric observations with atmospheric optical
path fluctuations. Each line corresponds to a different piston
sequence. For each sequence the interferogram, the modulus of the
spectrum, the phase of the spectrum and the piston perturbation are plotted
There are 1024 samples per sequence. Given the average wind speed v, the
scanning frequency 
, I first compute a Gaussian sequence of average 0 and
of standard deviation 1. This sequence is filtered with the piston power spectrum
given in Sect. 3.2 and is normalized to a standard deviation of
attenuated by the factor given by curves in Fig. 3. The
length of each sequence is 
m corresponding to a scan duration of
ms and yielding an attenuation factor of 0.57 and a standard deviation
of 
m. This final sequence is the opd fluctuation as a function of opd
x: 
. I then compute the nominal interferogram I(x) given in
Eq. (4) and normalized to an average of 1. Eventually, the pistoned
interferogram is 
. In interferometers, the
zero opd is computed relative to the knowledge of the metrology of the
system. It is known to within a constant which is the instrument
opd. We assume in the following that the instrument opd is zero (we
only consider the errors due to the atmosphere).
Figure 3 displays a set of four
interferograms simulating an observation of a 3500K blackbody spectrum star
with a resolution of 
cm
. On each line the first graph is the
interferogram followed by the modulus of the spectrum, the phase of
the spectrum and the piston
sequence. The speed of the fringes is 
mm s
yielding a fringe
frequency of 
Hz. The wind speed is 
m s
. The observing
conditions are supposed to be quite good with 
cm at 
m, hence
a seeing of 
arcsec. These parameters are hereafter referred to as the
nominal parameters and are listed in Table 1.
The first interferogram is
not pistoned. When comparing the pistoned ones to this one it is obvious that the
speed of the fringes is varying, some fringes being stretched while others are
compressed (hence the analogy with the mechanics term ``piston''), and that the
whole interferogram is shifted with a random position offset. The shape of the
modulus of the spectrum has changed. When piston is accelerating in the main lobe
of the interferogram, fringes are compressed which increases their apparent
frequency. The spectrum support is then shifted to higher frequencies and enlarged
as the envelope of the fringes is tightened. This is what can be seen on the
second sequence. The opposite behavior is seen on the third sequence where piston is
decelerating. The first derivative of piston thus shifts the interferogram in the
frequency domain. Higher orders even destroy low resolution information as shown
by the simulations. In the fourth sequence, the main lobe of fringes is only slightly
pistoned as it has been recorded during a phase when piston was flat. Its support
is in the correct range but the spectral information is destroyed. Concerning phase,
it is constant in the original interferogram whereas it is a function of
wavelength in the pistoned ones. It is dominated by a linear component because of the position
offset, but some higher order terms are introduced and are due to the asymmetry of
the interferograms.
These simulations clearly show that there is a poor
correlation between successive pistoned spectra and that spectral information such
as line strength cannot be recovered in a direct manner. Let us now focus on a
method to retrieve spectral information.