

Up: Correction of the
The aim of this section is essentially to provide the
reader with a few classical notations as well as basic concepts of
interferometry. Paragraph 2.1 is a brief theoretical tutorial on inteferometry.
The purpose of the Double Fourier interferometric mode probing both temporal and
spatial coherence properties of sources is explained in paragraph 2.2.
Eventually, paragraph 2.3 adresses the aim of this paper, that is to say the
nature of the disturbances generating optical path fluctuations.
Equations derivations are classical
and can be found in litterature (Goodman 1985 for example).
Nevertheless, I intend to give a fundamental subset of equations whose accurate
knowledge is mandatory for a good understanding of the remaining of the article. Let us
consider two pupils 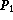 and
and  of an interferometer and the corresponding
sampled complex amplitudes of an astronomical wavefront
of an interferometer and the corresponding
sampled complex amplitudes of an astronomical wavefront  and
and
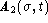 , where
, where  is the wavenumber and t is time. The two
amplitudes are combined and sent to a detector. The monochromatic energy
detected
at the output of the combiner is proportional to the average squared modulus (on
a time scale far greater than the period of the wave) of the sum of the two
fields:
is the wavenumber and t is time. The two
amplitudes are combined and sent to a detector. The monochromatic energy
detected
at the output of the combiner is proportional to the average squared modulus (on
a time scale far greater than the period of the wave) of the sum of the two
fields:

For sake of simplicity, all multiplicative coefficients (detector
gain, interferometer transmission, etc ...) will be set to one and their
expressions will be dropped in the following equations. The monochromatic energy
collected by the two pupils (which is proportionnal to the spectrum of the
source) is supposed to be the same and the normalized total energy over the
bandwidth is noted 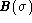 . Equation (1) is then rewritten as:
. Equation (1) is then rewritten as:
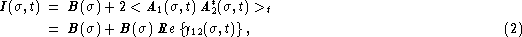
where  is the complex degree of coherence of
the two beams coming from the source and collected by the two pupils of the
interferometer. For a monochromatic radiation, it has a simple expression as a
function of the delay
is the complex degree of coherence of
the two beams coming from the source and collected by the two pupils of the
interferometer. For a monochromatic radiation, it has a simple expression as a
function of the delay  between the two beams (Goodman 1985):
between the two beams (Goodman 1985):

where v is the rate of change of opd. 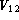 is the coherence factor
of the two beams or fringe visibility and is wavelength dependent. The value of
visibility is determined by the geometrical aspect of the source and by the
geometrical characteristics of the baseline. It is the Fourier transform
of the intensity distribution of the source at a spatial frequency equal
to the vector baseline over wavelength according to the Van Cittert-Zernike theorem
(Born & Wolf 1980; Goodman 1985).
Visibility
is the coherence factor
of the two beams or fringe visibility and is wavelength dependent. The value of
visibility is determined by the geometrical aspect of the source and by the
geometrical characteristics of the baseline. It is the Fourier transform
of the intensity distribution of the source at a spatial frequency equal
to the vector baseline over wavelength according to the Van Cittert-Zernike theorem
(Born & Wolf 1980; Goodman 1985).
Visibility is the observable measured by
interferometers.
is the observable measured by
interferometers.
It is equivalent to express delay either as a temporal delay  or as an
optical path difference x as the ratio of the two is the speed of the fringes
v. In wide band, Eq. (2) becomes:
or as an
optical path difference x as the ratio of the two is the speed of the fringes
v. In wide band, Eq. (2) becomes:

It is necessary to compensate delay of one the two beams with respect to the other one when
recording the interferogram because the coherence length, in wide band, is only
a few fringes. Monochromatic waves coherently interfere around the
equal optical path position when the optical paths of the two beams are matched by
a delay line.
The first term in Eq. (4) will be left aside in the following and I will only
consider the second one which is the modulated part of the interferogram. When
the complex spectrum is defined as the hermitian part of the spatio-temporal source
spectrum (modulus is an even function and phase is an odd function of
wavenumber):

the
modulated part of energy, noted  , gets a more convenient expression:
, gets a more convenient expression:

In other words, the Fourier transform of the modulated
interferometric signal is the complex spectrum of the astronomical source.
A few different ways of doing
interferometry (mostly depending on measured quantities) exist (see review by M.
Shao 1992). Some interferometers recombine beams in the pupil plane
whereas others are image plane oriented. Here, no distinction will be made between
these two different philosophies. Some interferometers (type I) are operated in the
long exposure mode, that is to say that a servoed delay line sets the optical path
difference (thereafter opd) to a constant value allowing the integration of the
interferometric signal to achieve high signal to noise (S/N) ratios on fringe
modulation. The value of the opd can be varied to scan through the whole interferogram.
Type II interferometers can be considered as short
exposure interferometers. The interferogram is acquired during a continuous scan
of the opd which is produced either by the Earth's rotation or by a
translating retroreflecting unit moving at a constant speed or by a combination
of the two. Integration is then no longer possible. Type I interferometers are not
opd fluctuation sensitive as the opd is servoed, whereas many factors can
introduce opd fluctuations in type II interferometers (this point will be
adressed in Sect. 2.3). Type II interferometers are
dedicated to spectral data analysis for they
naturally reach a higher spectral resolution while type
I data are reduced in direct space. These type II
interferometers are called Double Fourier
Interferometers (hereafter DFI) because they both probe
spatial and temporal coherence properties of the
light emitted by astrophysical sources (Itoh & Ohtsuka
1986; Mariotti & Ridgway 1988). Spatial information
is contained in the modulated energy of interferograms
as shown in Sect. 2.1 and is wavelength dependent. The
Fourier transform of the interferogram sequence yields
the source temporal spectrum rescaled by the visibility
function. It has been shown (Ridgway et al. 1986) that
an accurate knowledge of the visibility-wavelength relation would have fruitful astrophysical implications, as well as visibility as a function of spatial frequency. DFI allows the determination of the visibility as a function of wavelength and is the interferometric mode that is mostly concerned in the following of the paper.
As shown in
Eq. (6) an interferogram can be considered as a
temporal sequence whose Fourier transform is
proportionnal to the spectrum of the source. The two
conjugate variables are the opd (or time) in the direct
space and wavenumber (or frequency) in the Fourier
space; one shifts from one set of conjugate variables
to the other by multiplying or dividing by the speed of
the fringes. Thus opd varies linearly with time. This
is what one should expect in an ideal interferometer.
In reality this occurs in a different way. Opd does not
vary linearily with time. Some opd distortions are
introduced and have mechanical and atmospheric sources.
Vibrations of static optics on the beam path change its
length and make it oscillate. But they can be lowered
to an inoffensive magnitude by increasing the
stiffness of the optics and by absorbing vibrations.
Non-linearities in the motion of the retroreflecting
stage of the delay line cause opd to fluctuate but they
can also be cancelled out by servoing the speed of the
carriage supporting the retroreflector. Some fiercer
fluctuations are generated by atmospheric turbulence.
Here we assume that atmospheric perturbations of
wavefronts are reduced to the 0-order ones (the
spatially averaged pertubations on the pupil) and that
higher orders have been filtered out by using monomode
fibers for example (Coudé du Foresto & Ridgway
1991; Coudé du Foresto et al. 1992), by data
reduction or with adaptive optics. The 0-order term is
known as ``piston effect'' and opd fluctuations are
due to differential piston between two apertures of
the interferometer. But piston and differential piston
stand for the same physical phenomenon.
Opd
fluctuations result in the loss of the Fourier
relation between the spectrum and the interferogram sequence preventing physical information recovery from the spectrum. Figure 3 of Sect. 3 shows four simulated low resolution spectra. The first one is computed from an opd fluctuation free interferogram whereas the others simulate observed spectra with regular turbulence conditions. It is obvious that without any piston correction no accurate information can be extracted from these spectra. Besides, piston introduces a random shift of the central fringe of the interferogram preventing measurement of the exact phase of visibilities, the accurate knowledge of which being essential to reconstruct a high resolution image of the source.
If most sources of optical path fluctuations have negligeable effects, atmospheric
turbulence effects at optical wavelengths must be taken into account. It is
possible to artificially increase the length of coherent interferogram by
scanning at a high speed. Rapid scanning freezes piston but it does not
reduce its amplitude. Besides, fast scanning reduces the
instrumental visibility (hence the S/N ratio of the modulated signal) as the
detector response decreases with increasing frequencies. Turbulence opd fluctuations thus
turn out to be a strong limitation to optimum information extraction in optical
astronomical interferometry. In the following Sects. I will expose a method to
correct ``pistoned'' interferograms to retrieve the modulus of the spectrum and
the phase to within a constant. This method does not take into account the
possibility to retrieve the exact phase of visibilities and does not address
the issue of image reconstruction in interferometry.


Up: Correction of the
Copyright by the European Southern Observatory (ESO)
web@ed-phys.fr