The model contains many free parameters, which may be divided into two broad categories: physical (mass-loss rate, absorption cross-sections, etc.), and geometric (e.g., binary phase, binary separation). In Sect. 7 (click here) (et seq.) the parameter sensitivity of the Raman-scattered lines is investigated by examining the changes to the Raman-line polarization spectrum resulting from changes in the system parameters. Since there is such a large number of free parameters it is not feasible to construct a complete grid of models, as this would require an impracticable computational expense. Instead we have constructed a benchmark reference model, and have studied the effects of changing the free parameters of that model.
Figure 2: Results for the reference model (
6825 Åline),
viewed at quadrature (Sect. 6): a),
b) are the normalized
Q, U images, scaled linearly over the range -1,+1:
c), the I image,
logarithmically scaled over a range of three decades; and
d), 
, scaled linearly over
the range 0,+1.
The O VI source is at +5,0, and the cool component (visible
as an occulting body in the I image) is at 0,0
The mass-loss rate of the red-giant star is expected to be an important
free parameter. Mass-loss rates for such stars are not generally
well known, but
Seaquist & Taylor (1990) used VLA 6-cm radio
observations to estimate values for several of the stars surveyed in
Paper I.
These mass-loss rates
are summarized in Table 2 (click here); they
cluster about a value of order 
yr
.
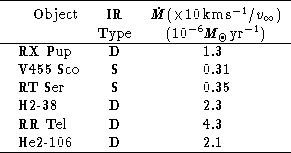
Table 2: Radio mass-loss rates for symbiotic stars (from Seaquist &
Taylor 1990)
There are, evidently, selection effects in operation,
since high mass-loss rates are required before the radio emission, which
originates in the volume of the red-giant wind ionized by the hot component,
becomes detectable. However, there are other lines of evidence which suggest
that the cool components in symbiotic systems undergo relatively high mass-loss
rates compared to
local bright M giants (Kenyon & Fernandez-Castro
1987; Kenyon 1988), and are
more similar to those of the `Bulge-like' M giants (Whitelock & Munari 1992).
We adopt 
for the reference model.
An explicit value is required for the photospheric radius (and for the
wind acceleration) in order to translate the mass-loss rate into a
density, through Eq. (1 (click here)). We adopted a value of
for the red-giant radius (e.g., Vogel 1991). For a
red-giant mass of 
, a mass ratio of 
1, and a
binary period of 
1 year (a `short-period', S-type system), the binary
separation factor, 
, is then 
5.
The overall scattering geometry is unaffected by simple scalings;
that is, similar results will be obtained for models which have the same
values of both 
and 
.
The outflow velocities of the red-giant winds are poorly known. A
canonical value of 10 kms
, based on CO lines formed at large
distances from the photosphere, is frequently adopted in the literature
(cf., e.g., Loup et al. 1993), but may not be appropriate for the
giants in symbiotic systems. For our reference model we adopt a
constant-velocity outflow, with 
kms
. The constant-velocity model allows a simple
analytical derivation of the path length for given optical depth between
any two arbitrary points in the flow (cf. Eq. 11 (click here)), and
the relatively high outflow speed more clearly reveals the velocity
structure in the lines. Moreover, there is some evidence in the
observations for relatively high-speed winds, as discussed below.
The opacities of the atmospheres of red giants are difficult to
calculate, due to the large number of molecular transitions. Recent
calculations by Allard & Hauschildt (personal communication) suggest
that the absorption opacity in the red (
7000 Å) is negligible,
and in the UV is in the range 0-10 (in units of the scattering
cross-section). The opacities in the UV and at the Raman wavelengths
are set to zero for the reference model, although the effects of finite
absorption at both wavelengths are investigated later.
There is direct observational evidence for fast winds from the hot
component in a few symbiotic systems, with outflow speeds of order
kms
(e.g., Nussbaumer et al. 1995). If the
OVI source arose in material with such large velocities, any
structure in the Raman lines would be completely smeared out (and the
lines would be enormously broad). The presence of resolved structure in
the Raman lines (Paper I) therefore immediately indicates that most
parent photons arise in material which has relatively small, HII-region-like thermal (and `turbulent') broadening, rather than
originating throughout a hot-component wind. This inference is
confirmed by recent observations of relatively narrow OVI
resonance lines in RR Tel (Espey et al. 1995).
Available observations of the OVI doublet in symbiotic
systems do not resolve the line widths, but high-resolution IUE
observations of resonance lines of other highly-ionized species, such as
NV, suggest line widths 
60 kms
FWHM
(e.g., Kindl et al. 1982; Penston et al. 1983). The profiles not
unusually show structure which may be of a P-Cygni nature (e.g., Viotti
et al. 1983; Michalitsianos et al. 1988)
or which may be associated with intrasystem absorption
(Shore & Aufdenberg 1993). For simplicity, we adopt a gaussian
distribution for the velocities of particles giving rise to the
OVI photons (other frequency distributions may easily be
specified), using the GASDEV subroutine of Press et al. (1989) to
calculate the deviates. In order to emphasize the structure resulting
from velocity fields in the red-giant wind, we take the lines in the
reference model to have a relatively low FWHM, 20 kms
, and a
mean value of zero (although we explore the consequences of adopting
other values).
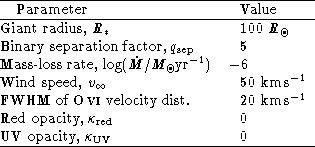
Table 3: The adopted parameters for
the reference model