

Up: Analysis of isoplanatic high
Subsections
The accuracy of the PSF estimate is primary in StarFinder, since the PSF
array is used as a template for all the stars in the image to be analyzed.
The user selects the most suitable stars, which are background subtracted,
cleaned from the most contaminating sources around, centered with sub-pixel
accuracy, normalized and superposed with a median operation. The centering
is performed by an iterative shift of the stellar image in order to cancel
the sub-pixel offset of its centroid (see
Christou & Bonaccini 1996).
The median operation, which is performed pixel-by-pixel, is preferred to
the mean because it is less sensitive to anomalous pixels (outliers) which
might appear in one or more stellar images among the selected ones. The
retrieved PSF is post-processed in order to reject any
residual spurious feature and to smooth the noise in the extended halo.
The PSF extraction procedure also reconstructs the
core of saturated stars by replacing the corrupted pixels with the central part
of the PSF estimate. Accurate positioning is achieved by means of
a cross-correlation technique, while the scaling factor is determined
with a least squares fit to the wings of the star to
repair. For a detailed description of the procedure, see Sect. 3.5.
At first we build a list of objects, the presumed stars, which satisfy the
condition
where i(x,y) is the observed intensity, b(x,y) the background emission
and t a fair detection threshold.
The presumed stars are analyzed one
by one by decreasing intensity. To illustrate a generic step of the
analysis, we consider the (n+1)-th object in the list, after the examination
of
the first n. A small sub-image of fixed size is extracted around the
object (Fig. 1, left).
![\begin{figure}
\par\includegraphics[width=14cm,clip]{1908f1.eps}\end{figure}](/articles/aas/full/2000/20/ds1908/Timg6.gif) |
Figure 1:
Left: sub-image extracted from a simulated stellar field. The
crosses indicate the objects within the region of interest: a central star (to
be analyzed in the current step), a brighter source (already known), a fainter
one (to be examined later) and the PSF feature of a much brighter star,
represented by the structure in the upper-left part of the sub-image.
Right: corresponding sub-region
extracted from the stellar field model, containing one replica of the PSF for
each star detected so far |
This sub-image may contain brighter stars
formerly analyzed, fainter objects
neglected in the current step and features of other stars lying outside the
sub-image. The information on the brighter sources is recorded in a synthetic
stellar field (Fig. 1, right), defined as the sum of two terms:
a superposition of PSF replicas, one for each star detected up to this point,
and an estimate of the background, assumed to be non uniform in
general.
The local contribution due to the brighter stars and the background, derived
from the synthetic field, is subtracted from the sub-image.
If a statistically significant residual remains, it
is compared to the central core of the PSF by means of a correlation
check. If the correlation coefficient is higher than a pre-fixed threshold then
the object of interest is rated similar to the PSF and accepted. The
accurate determination of its position and relative flux is attained by means of
a local fit, in which the observed sub-image is
approximated with the multi-component model described in Sect. 3.6.
The actual size of the fitting region is comparable to the diameter of the
first diffraction ring of the PSF. This choice ensures that the information
represented by the shape of a high-Strehl PSF is included in the fitting process
to achieve better accuracy and prevents the growth of the number of sources to
be fitted together. For the central object of our example a single component fit
is performed and the contribution due to the brighter stars is considered as a
fixed additive term. A multi-component fit is performed when
the star is in a very compact group, at separations comparable to the
PSF FWHM.
If the fit is acceptable, the parameters of the new detected star are
saved and those of the already known sources,
which have been possibly re-fitted, are upgraded. The new star and an upgrade of
the re-fitted sources are added to the synthetic field.
This analysis is performed for each object in the initial list (a flow-chart
illustrating the operations of StarFinder is in Fig. 2).
![\begin{figure}
\par\includegraphics[width=14cm,clip]{1908f2.eps}\end{figure}](/articles/aas/full/2000/20/ds1908/Timg7.gif) |
Figure 2:
Flow-chart of the algorithm for stars detection and analysis |
To achieve
a better astrometric and photometric accuracy, at the end of the examination of
all the objects, the detected stars are fitted again, this time considering all
the known sources. This step may be iterated
a pre-fixed
number of times or until a convergence condition is met.
At the end of the analysis, it is possible to stop the algorithm or instead
perform a new search for lost objects removing the detected stars and using
an upgraded background estimate. It should be
stressed that this image subtraction is just a tool to highlight significant
residuals. Any further analysis is performed on the
original frame, in order to take into account the effects arising from the
superposition of the PSFs of neighboring sources. Generally, after
2-3 iterations of the main loop, the number of
detected stars approaches a stable
value.
A binary star with different separation values (Fig. 3) has
been simulated to show how the code works with crowded sources.
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{1908f3.eps}\end{figure}](/articles/aas/full/2000/20/ds1908/Timg8.gif) |
Figure 3:
Simulated binary stars at various separations. From left to right,
top to bottom the separation is 2, 1, 0.75, 0.5 times the PSF
FWHM. For all the images the flux ratio is 2:1 |
With a separation of 2 PSF FWHM the two components are well separated and the
code analyzes them with the standard procedure described in the previous
sub-section. In the other cases (separation from 1 to 0.5 PSF FWHM) the
secondary component is not detected as a separate relative maximum and
it is lost. However, if the separation is not as small as 0.5 FWHM, a further
iteration of the main loop enables the algorithm to detect the fainter
component by subtracting the brighter one. This strategy forces the
two stars to pass the correlation test, the principal component as a
presumed single object and the secondary in a subsequent iteration of the
loop.
In a way the iteration of the main loop is a de-blending strategy,
because it enables the algorithm to detect stars whose intensity peak
is not directly visible in the observed data.
This strategy fails when:
- the binary is very noisy and the two components have similar flux. In a
similar situation the principal component may not pass the correlation test,
preventing also the detection of the secondary in a further iteration. These
noisy blends may be recovered at the end of the overall analysis;
- The two components are almost equally bright and have a separation close
to the lower limit (1/2 PSF FWHM). The residual corresponding to the
secondary after subtracting the principal component may have a distorted shape
and might not pass the correlation check.
The latter case may be handled by a method based on a thresholding
technique. The object is cut at a prefixed level, about 20% below
the central peak, and transformed to a binary array, setting to 1 all the pixel
above the threshold and to 0 the pixels below. If the area of the pixels with
value 1 is more extended than the PSF, the object is considered a blend and
the secondary star may be detected by subtracting the brighter one;
then a two-component fit allows accurate astrometry and photometry of the
two sources. This strategy can be iteratively applied to multiple blends.
It should be stressed that the area measurement is not reliable when the
value of the cutting threshold is comparable to the noise level: for this
reason the de-blending procedure is applied only to objects with a suitable
signal-to-noise ratio. Moreover the area measurement is reliable when the
data are adequately sampled. This de-blending procedure is applied at the
end of the last iteration of the main loop, when all the resolved sources
have been detected: in this way the probability that a single object may
appear artificially blurred because of the contamination of still unknown
sources is largely reduced.
In a normal case, like the simulated field of
Sect. 4.1, two or three iterations of the main loop find almost all
(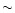 99%) the
stars that StarFinder may detect. The de-blending procedure described above
adds
99%) the
stars that StarFinder may detect. The de-blending procedure described above
adds 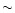 1% more stars, without additional false detection. The number of
lost objects belonging to the first category described above is negligible
(
1% more stars, without additional false detection. The number of
lost objects belonging to the first category described above is negligible
(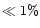 ).
).
Normally we perform two or three iterations of the main
loop and apply the de-blending strategy only in very crowded fields.


Up: Analysis of isoplanatic high
Copyright The European Southern Observatory (ESO)
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{1908f3.eps}\end{figure}](/articles/aas/full/2000/20/ds1908/Timg8.gif)
![]() 99%) the
stars that StarFinder may detect. The de-blending procedure described above
adds
99%) the
stars that StarFinder may detect. The de-blending procedure described above
adds ![]() 1% more stars, without additional false detection. The number of
lost objects belonging to the first category described above is negligible
(
1% more stars, without additional false detection. The number of
lost objects belonging to the first category described above is negligible
(![]() ).
).