![$\displaystyle %
c(a,b) =
\frac{\sum_{x,y}\left[ i\left( x,y\right) -\bar{\imath...
...ht]^{2}}\sqrt{\sum_{x,y} \left[ p\left( x-a,y-
b\right) -
\bar{p}\right] ^{2}}}$](/articles/aas/full/2000/20/ds1908/img11.gif) |
(2) |
StarFinder includes an automatic procedure to repair known bad pixels, which are replaced with the median of the good data points in a suitable neighborhood. The use of this procedure is particularly recommended in the extraction of the PSF. Indeed the stellar images, which will be combined to form the PSF, are centered with sub-pixel accuracy by means of an interpolation technique and the presence of bad pixels may produce unpredictable interpolation errors. Even if replaced, the bad pixels are excluded from any further computation concerning the correlation coefficient and the fitting process.
A reliable estimate of the background is necessary to define the detection condition and to compute the correlation coefficient of the presumed stars with the PSF.
A straightforward technique to estimate the background is to smooth the image by median filtering, replacing each pixel with the median computed over a suitable neighborhood, of size comparable to the characteristic width of a stellar image. This method tends to over-estimate the background underneath strong peaks. A more accurate approximation, even in crowded fields, is described in Bertin & Arnouts (1996). The image is partitioned in sub-regions arranged in a regular grid and a local estimate is calculated for each sub-patch by means of an IDL implementation of the DAOPHOT SKY routine (Stetson 1987), due to Landsman (1995). This array of sky measurements is smoothed by median filtering and interpolated onto the same grid of the input image.
It should be stressed that the background computation is unavoidably affected by the presence of bright sources. In general a more accurate estimate can be obtained after the analysis of the stellar field, when the most contaminating sources are known and can be subtracted.
The estimate of the noise is useful to define the detection threshold and to compute the formal errors on the retrieved astrometry and photometry.
The overall effect of photon and instrumental noise can be computed if the required parameters (detector gain, read-out-noise, dark current, etc.) are known. Otherwise an estimate of the mean background noise can still be obtained by means of histogram fitting techniques (Almoznino et al. 1993; Bijaoui 1980). Assuming that the intensity of the sky radiation is distributed normally around a typical value, the histogram of the observed intensity levels should be quite similar to a Gaussian distribution, whose mode and standard deviation represent respectively the sky value and the associated noise. Actually the contamination due to the stellar sources produces a high-intensity tail and an artificial broadening of the histogram, which prevents an accurate estimate of the background noise. This problem can be partially overcome by removing the signal from the image, leaving only the pixel-to-pixel variations associated to pure noise: a reasonable estimate of the signal to subtract for this purpose can be obtained by smoothing the data with a median filtering technique. After this operation the histogram is symmetric around its mode and the background noise standard deviation can be estimated by means of a Gaussian fit to the histogram itself.
False detections, associated to noise spikes or residual PSF features of
bright stars, are recognized on the basis of their
low correlation coefficient with the PSF, which represents a template for
each true star in the image. The correlation coefficient (Gonzalez & Woods
1992) is defined as
![$\displaystyle %
c(a,b) =
\frac{\sum_{x,y}\left[ i\left( x,y\right) -\bar{\imath...
...ht]^{2}}\sqrt{\sum_{x,y} \left[ p\left( x-a,y-
b\right) -
\bar{p}\right] ^{2}}}$](/articles/aas/full/2000/20/ds1908/img11.gif) |
(2) |
The correlation coefficient is computed on the core of the PSF: typically the central spike of the diffraction pattern is considered, out to the first dark ring. A fair correlation threshold must be fixed in order to discriminate and reject unlikely detections, without losing faint stars contaminated by the background noise; a value of 0.7 or 0.8 is acceptable in most cases.
The correlation coefficient represents also an effective tool to select the stars with the highest photometric reliability, since generally a very high correlation value is associated to resolved single sources.
Saturated stars provide precious information on the PSF halo, so it may be useful to include them, appropriately reconstructed, in the PSF extraction process. In addition, the repaired saturated stars can be recognized by the star detection algorithm and their contribution be taken into account during the analysis of near and fainter sources.
The core of a saturated star is replaced with a shifted scaled replica of a
preliminary estimate of the PSF. The repaired star is defined as
![\begin{displaymath}%
i_{\rm rep.}(x,y)=
\left\{
\begin{array}{ll}
i(x,y) & \mbo...
...m]
f p(x-x_{0},y-y_{0}) & \mbox{otherwise}
\end{array}\right.
\end{displaymath}](/articles/aas/full/2000/20/ds1908/img14.gif) |
(3) |
This procedure has been applied to the brightest star (IRS 7) of the Galactic
Center
image shown in Sect. 4.2. This source is not
saturated in the original data, but it has been artificially corrupted
by an upper cut at half maximum. The repair procedure
is able to reconstruct the original peak with an error of ![]() 5%,
imposing a positioning accuracy of 1/2 pixel.
5%,
imposing a positioning accuracy of 1/2 pixel.
A sub-image centered on the star of interest is extracted and
approximated with the model
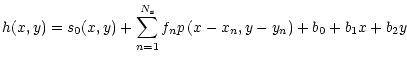 |
(4) |
| (5) |
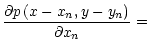 | |||
![$\displaystyle {\rm FT}^{-1}\left[ {\rm FT}\left[ p\left( x,y\right) \right]{\rm...
...-i2\pi
\left(ux_{n}+vy_{n}\right) /N}\left(-i \frac{2\pi u}{N} \right)\right] =$](/articles/aas/full/2000/20/ds1908/img19.gif) |
|||
![$\displaystyle {\rm FT}^{-1}\left[ \left( -i\frac{2\pi u}{N}\right) {\rm FT}\left[ p\left(x-x_{n},y-
y_{n}\right) \right] \right]$](/articles/aas/full/2000/20/ds1908/img20.gif) |
(6) | ||
![\begin{figure}
\par\includegraphics[width=13cm,clip]{1908f4.eps}\end{figure}](/articles/aas/full/2000/20/ds1908/Timg21.gif) |
Figure 4:
Synthetic field image with 1000 sources. The PSF Strehl ratio is
|
A band-limited function in
one dimension is Nyquist-sampled if the step size
fulfills the condition
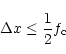 |
(7) |
Even though the interpolation of the PSF array is allowed only on Nyquist-sampled data, the cubic convolution technique seems to produce acceptable results even with marginally under-sampled images. Tests performed on Airy diffraction patterns, with a sampling step twice as large as the critical sampling step size, indicate that the interpolation-induced oscillations amount to a few percent of the image peak, as opposed to 10-20% of other interpolation techniques like Fourier shift or bicubic splines.
Copyright The European Southern Observatory (ESO)