

Up: Period changes in W Sextantis
The eclipsing binary DK Cyg
(also BD
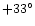 4304, HIP 106574, AN 1.1927, FL 3231;
4304, HIP 106574, AN 1.1927, FL 3231;
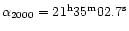 ,
,
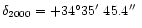 ,
,
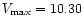 mag; Sp. A8V)
is a well-known W UMa-type binary with a period of about 0.4707 days.
It was discovered to be a variable by
Guthnick & Prager (1927).
The first photoelectric observations were made by
Hinderer (1960).
Binnendijk (1964) in his photometric study derived linear light
elements:
mag; Sp. A8V)
is a well-known W UMa-type binary with a period of about 0.4707 days.
It was discovered to be a variable by
Guthnick & Prager (1927).
The first photoelectric observations were made by
Hinderer (1960).
Binnendijk (1964) in his photometric study derived linear light
elements:
and found the change of the secondary minimum depth.
The period study of DK Cyg was published by
Paparo et al. (1985). They showed that the orbital period was increasing and
calculated the first parabolic light elements:
The next photoelectric study was published by Awadalla (1994)
who refined the light elements:
and confirmed the light curve variability.
See also that paper for further details and a historical
review of other observations.
The first spectroscopic study and radial velocity curve analysis
was presented by
Rucinski & Lu (1999) who found
q = m2/m1 = 0.325.
Recently, updated linear ephemeris of DK Cyg was presented by
Kiss et al. (1999):
All photoelectric times of minimum light published in
Hinderer (1960),
Binnendijk (1964),
Paparo et al. (1985),
Agerer (1988, 1990, 1992),
Awadalla (1994),
Agerer & Hübscher (1995, 1996) and
Hegedüs et al. (1996),
as well as new timings given in Table 1 were incorporated
in our analysis. One additional time of primary minimum was obtained
by J. Strobl at the Jindrichuv Hradec Observatory,
Czech Republic,
with a CCD camera SBIG ST6 and a 16 cm Newtonian telescope. Other numerous
visual and photographic estimations obtained by the AAVSO, BAV and BBSAG
observers were used with less weight.
A total of 95 times of minimum were incorporated in our
analysis. Using the method of least squares we derived the following light
elements with a quadratic term:
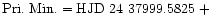
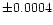
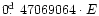 +
+
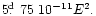
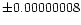
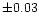
The O-C residuals for all times of minimum with respect
to the linear ephemeris are shown in Fig. 1.
![\begin{figure}
\centering
\includegraphics[width=8.5cm,clip]{DKCYG.EPS}\end{figure}](/articles/aas/full/2000/20/ds10133/Timg24.gif) |
Figure 1:
O-C residuals for the times of minimum of DK Cyg
with respect to the linear light elements.
The continuous curve represents the parabolic approximation.
The individual photoelectric times are denoted by dots,
photographic or visual estimations by circles |
The non-linear fit,
corresponding to the light elements given above, is plotted as
a continuous curve. The period increase resulting from these elements
is
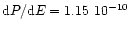 day/cycle or
day/cycle or
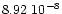 day/year or 0.8 seconds/century.
Because the long-term increase in orbital period is usually explained
by mass transfer from the secondary to the primary component, we calculated
the value of this supposed mass transfer for DK Cyg. If the mass
transfer is conservative with no magnetic field we determine the mass
transfer rate
day/year or 0.8 seconds/century.
Because the long-term increase in orbital period is usually explained
by mass transfer from the secondary to the primary component, we calculated
the value of this supposed mass transfer for DK Cyg. If the mass
transfer is conservative with no magnetic field we determine the mass
transfer rate
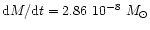 /year for
a total mass of the system
/year for
a total mass of the system
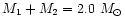 and the mass ratio
q = 0.325 (Rucinski & Lu 1999).
and the mass ratio
q = 0.325 (Rucinski & Lu 1999).


Up: Period changes in W Sextantis
Copyright The European Southern Observatory (ESO)
![]() 4304, HIP 106574, AN 1.1927, FL 3231;
4304, HIP 106574, AN 1.1927, FL 3231;
![]() ,
,
![]() ,
,
![]() mag; Sp. A8V)
is a well-known W UMa-type binary with a period of about 0.4707 days.
It was discovered to be a variable by
Guthnick & Prager (1927).
The first photoelectric observations were made by
Hinderer (1960).
Binnendijk (1964) in his photometric study derived linear light
elements:
mag; Sp. A8V)
is a well-known W UMa-type binary with a period of about 0.4707 days.
It was discovered to be a variable by
Guthnick & Prager (1927).
The first photoelectric observations were made by
Hinderer (1960).
Binnendijk (1964) in his photometric study derived linear light
elements:
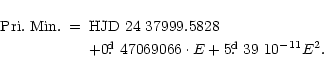
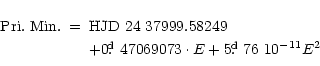
![]()
![]()
![]() +
+
![]()
![]()
![]()