The eclipsing binary V401 Cyg
(also BD
![]() 3592, HIP 95816, AN 88.1929, FL 2747, P1824;
3592, HIP 95816, AN 88.1929, FL 2747, P1824;
![]() ,
,
![]() ,
,
![]() 10.8 mag; Sp. F0)
is a relatively well-known W UMa-type binary with period of about 0.58 days.
It was discovered to be a variable by
Hoffmeister (1929) and for a long
time it was misclassified as RR Lyrae type variable with period 0.2895 days.
Lurye (1947) found its eclipsing binary nature and derived the light
elements with the correct period:
10.8 mag; Sp. F0)
is a relatively well-known W UMa-type binary with period of about 0.58 days.
It was discovered to be a variable by
Hoffmeister (1929) and for a long
time it was misclassified as RR Lyrae type variable with period 0.2895 days.
Lurye (1947) found its eclipsing binary nature and derived the light
elements with the correct period:
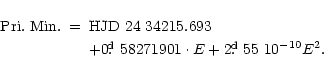


![\begin{figure}
\includegraphics[width=8.5cm,clip]{401CYG.EPS}\end{figure}](/articles/aas/full/2000/20/ds10133/Timg37.gif) |
Figure 2: O-C graph for V401 Cyg. See legend for Fig. 1 |
The B and V light curves of V401 Cyg published by Purgathofer (1964),
as well as our R light curve, have been used simultaneously for the
determination of the geometric and photometric elements using the Binary
Maker 2.0 reduction software (Bradstreet 1993).
This program, based on the Wilson-Devinney algorithm, is used for
a preliminary analysis of light curves by graphically producing models
of close binaries. First, the observed points
ordered in phase were combined into 177 normalized binned points in each
colour. Based on the GCVS's spectral classification of the primary
component, F0, and the colour index
B - V=0.36 mag (Purgathofer 1964),
the temperature was adopted to be T1=6700 K.
The other adopted parameters are the
gravity-darkening coefficients g1 = g2,
the albedoes A1 = A2 and
the linear limb-darkening coeficients x1 and x2.
We adjusted the following parameters:
the mass ratio
q = M2/M1,
the potential function ![]() ,
,
![]() ,
the temperature of the secondary component T2,
and the orbital inclination i.
The final solution is given in Table 2; the uncertainty in the
inclination is about
,
the temperature of the secondary component T2,
and the orbital inclination i.
The final solution is given in Table 2; the uncertainty in the
inclination is about ![]() degrees and the difference in temperature
is known to about
degrees and the difference in temperature
is known to about ![]() ,
both dependent on the mass ratio.
,
both dependent on the mass ratio.
![\begin{figure}
\centering
\includegraphics[width=7.0cm,clip]{401LCV.EPS}\end{figure}](/articles/aas/full/2000/20/ds10133/Timg50.gif) |
Figure 3: V light curve of V401 Cyg obtained by Purgathofer (1964). The continuous line represents the light-curve solution with parameters given in Table 2. The shift of the secondary minimum from the phase 0.5 is clearly visible |
![\begin{figure}
\centering
\includegraphics[width=7.0cm,clip]{401R.EPS}\end{figure}](/articles/aas/full/2000/20/ds10133/Timg52.gif) |
Figure 4: A plot of the differential R-magnitudes of V401 Cyg obtained during the secondary eclipse at JD 24 51738 |
Copyright The European Southern Observatory (ESO)