

Up: Blind source separation and
After a set of tests we noticed that the previous tools were not
sufficient to select the best BSS. We introduced another test
based on the mutual information between the sources.
Let us consider two sources S1 and S2. Their entropies are
defined as:
| E(S1) |
= |
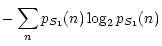 |
(16) |
| E(S2) |
= |
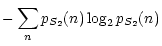 |
(17) |
where
pS1(n) and
pS2(n) are the probabilities of the
pixel value n respectively in sources S1 and S2.
The entropy of the couple S1 and S2 is:
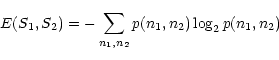 |
(18) |
where
p(n1,n2) is the joint probability of pixel value n1for S1 and n2 for S2. If the sources are independent:
|
E(S1,S2)=E(S1)+E(S2).
|
(19) |
The quantity:
|
I(S1,S2)=E(S1)+E(S2)-E(S1,S2)
|
(20) |
is called the mutual information between S1 and S2. It is
the information on S1 knowing S2 and inversely (Rényi
1966). From Eqs. (16-18) and
(20)
I(S1,S2) can be written as:
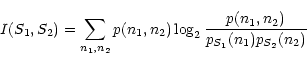 |
(21) |
which is the Kullback-Leibler divergence between the joint
probability and the probability obtained from the marginal
probabilities (Comon 1994). If the sources are independent, the
joint probability is the product of the marginal ones and this
divergence is equal to 0.
Then, the mutual information of a set of l sources is defined as
a generalization of Eq. (21). We have:
The observed SMI can be derived from Eq. (22). We
have to extract from experimental data an available estimation of
the probability
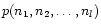 .
This probability is
obtained from the number of pixels having a value n1 in source
S1, n2 in source S2,
.
This probability is
obtained from the number of pixels having a value n1 in source
S1, n2 in source S2,  ,
nl in source Sl.
Then we distribute the pixels among Kl cells, where Kcorresponds to the number of levels per source.
,
nl in source Sl.
Then we distribute the pixels among Kl cells, where Kcorresponds to the number of levels per source.
As Kl increases exponentially with the number of sources, the
mean number of pixels per cell decreases rapidly with l, and
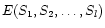 is badly estimated. In order to avoid this
difficulty, we notice that we do not need to compute the exact
value
is badly estimated. In order to avoid this
difficulty, we notice that we do not need to compute the exact
value
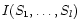 ,
but only to say for which mixing matrix
A or its inverse B=A-1, the mutual information is minimum.
We can write the approximation:
,
but only to say for which mixing matrix
A or its inverse B=A-1, the mutual information is minimum.
We can write the approximation:
We obtain the sources from the images from a linear
transformation, since the entropy of the source set
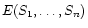 is the entropy of the image set
is the entropy of the image set
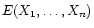 plus the logarithm of the Jacobian of the
transformation:
plus the logarithm of the Jacobian of the
transformation:
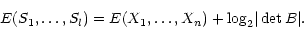 |
(24) |
We obtain:
Equation (23), and consequently
Eq. (25) are true only as a limit for an increasing number
of pixels. This number must be such that it allows one to get an
experimental PDF with a very small sampling interval. Then it is
sufficient to minimize the function (Comon 1994):
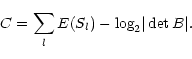 |
(26) |
We applied Eq. (26) and the optimal set of sources
was not the one retained by visual inspection. The drawback in
Eq. (26) is that we never have enough pixels to
validate it. We preferred to define SMI by summing the pairwise
mutual information values, as explained below.
The entropy depends on the coding step between two levels:
- -
- If the step is too small the
number of pixels per cell is too low and then the estimation is
not available;
- -
- If the step is too large, the entropy is too small, the PDF is smoothed
and it is not
sensitive to non-Gaussian features.
Then the SMI determination is achieved in four steps:
- 1.
- For each source i we determine the mean value mi and the standard
deviation
 after a
after a 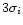 clipping. In this
algorithm we compute iteratively these parameters and we reject
the values outside the interval
clipping. In this
algorithm we compute iteratively these parameters and we reject
the values outside the interval
![$[m_i-3\sigma_i,m_i+3\sigma_i]$](/articles/aas/full/2000/19/ds9958/img71.gif) .
After a few iterations (4 to 5) the algorithm converges. In
the case of a true Gaussian distribution, the obtained mean is
correct, while the
.
After a few iterations (4 to 5) the algorithm converges. In
the case of a true Gaussian distribution, the obtained mean is
correct, while the 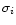 bias is of the order of
bias is of the order of 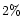 .
If we
are not dealing with a Gaussian distribution, these parameters
define a Gaussian kernel of the PDF, and we will measure more
values outside the interval
.
If we
are not dealing with a Gaussian distribution, these parameters
define a Gaussian kernel of the PDF, and we will measure more
values outside the interval
![$[m_i-3\sigma_i,m_i+3\sigma_i]$](/articles/aas/full/2000/19/ds9958/img71.gif) than
for a Gaussian PDF;
than
for a Gaussian PDF;
- 2.
- The histogram Hi(k) of source i is determined with a cell size
equal to this deviation
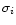 .
We evaluate the entropy of the
source Ei by:
.
We evaluate the entropy of the
source Ei by:
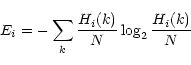 |
(27) |
where N is the number of pixels;
- 3.
- We determine then the mutual histogram Hij with the
same cell size, and we compute the resulting entropy Eij. The
mutual information between i and j is equal to:
This mutual information is independent of the cell size, for
values smaller than 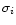 ,
for a large number of pixels. A
faint bias is introduced for a small number of pixels per cell. It
is a possible compromise to choose a cell size equal to
,
for a large number of pixels. A
faint bias is introduced for a small number of pixels per cell. It
is a possible compromise to choose a cell size equal to
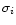 ;
;
- 4.
- We quantify the quality of each separation by the sum:
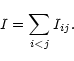 |
(29) |
We note that I only takes into account the pixel PDF. Therefore
it favors the algorithms based on PDF, such as KL, JADE and
FastICA, and penalizes SOBI.


Up: Blind source separation and
Copyright The European Southern Observatory (ESO)
![]() is badly estimated. In order to avoid this
difficulty, we notice that we do not need to compute the exact
value
is badly estimated. In order to avoid this
difficulty, we notice that we do not need to compute the exact
value
![]() ,
but only to say for which mixing matrix
A or its inverse B=A-1, the mutual information is minimum.
We can write the approximation:
,
but only to say for which mixing matrix
A or its inverse B=A-1, the mutual information is minimum.
We can write the approximation: