| Mc(ti) = | |||
| (25) |
In the second group of experiments we
used the parameters of a two-harmonic fit to the real light curve
of ER Vul, which were estimated previously
(You 1999). The corresponding amplitudes and error levels
are given in Table 2 and the light curves
are shown in Fig. 2.
The most important difference between
the two groups of simulations is the relatively low amplitude
of the first harmonic in the second group.
Finally, to the computed trigonometric polynomials
we added normally distributed uncorrelated noise Ni(0,1)
which
we computed using a random number generator:
To test the new method, both the multichannel PDM and
the single channel PDM were applied for all channels
of the two groups of simulations. In the first place,
we wanted to compare the detection capabilities of
the multichannel method to that of the single channel analysis.
This is why we chose a relatively narrow period search range
![]() and
and
![]() .
In this way the real period buried in the noise
will basically "compete'' only with the random fluctuations.
A more comprehensive search where spurious periods are taken into account
seriously is described afterwards.
.
In this way the real period buried in the noise
will basically "compete'' only with the random fluctuations.
A more comprehensive search where spurious periods are taken into account
seriously is described afterwards.
For the smoothing criterion L(tij), we adopted
![]() and
for the selection criterion
g(tij,P) we set
and
for the selection criterion
g(tij,P) we set
![]() according to the above adopted models.
These are typical values and do not depend strongly
on the data to be analysed.
according to the above adopted models.
These are typical values and do not depend strongly
on the data to be analysed.
| Set | Noise |
|
|
|
|
|
|
|
| 1 | 0.01Ec | 1.43 | 1.53 | 1.63 | 1.78 | 0.698 | 0.69810094 | 0.69809942 |
| 2 | 0.1Ec | 0.41 | 0.49 | 0.60 | 0.77 | 0.698 | 0.69810094 | 0.6981014 |
| 3 | 0.25Ec | 0.03 | 0.08 | 0.22 | 0.35 | 0.698 | 0.69809550 | 0.6980980 |
| 4 | 0.5Ec | -0.25 | -0.19 | -0.05 | 0.06 | 0.698 | 0.69810094 | 0.6980991 |
| 5 | 0.75Ec | -0.45 | -0.34 | -0.22 | -0.10 | 0.698 | 0.69810094 | 0.698099 |
| 6 | 1.0Ec | -0.53 | -0.49 | -0.39 | -0.23 | 0.698 | 0.69807374 | 0.698075 |
| 7 | 1.25Ec | -0.68 | -0.57 | -0.47 | -0.36 | 0.698 | 0.69809006 | 0.698088 |
| 8 | 1.5Ec | -0.75 | -0.65 | -0.55 | -0.40 | 0.697 | 0.69811130 | 0.698109 |
| 9 | 1.75Ec | -0.79 | -0.71 | -0.57 | -0.48 | 0.697 | 0.69810586 | 0.698108 |
| 10 | 2.0Ec | -0.84 | -0.82 | -0.65 | -0.53 | 0.698 | 0.69816081 | 0.698162 |
| 11 | 2.25Ec | -0.88 | -0.83 | -0.72 | -0.58 | 0.697 | 0.69816570 | 0.698166 |
| 12 | 2.5Ec | -0.94 | -0.88 | -0.76 | -0.66 | -- | -- | -- |
| Set | Noise |
|
|
|
|
|
|
|
| 1 | 0.01Ec | 1.75 | 1.98 | 1.92 | 1.91 | 0.698 | 0.69809688 | 0.698099296 |
| 2 | 0.1Ec | 0.96 | 1.33 | 1.29 | 1.27 | 0.698 | 0.69809688 | 0.69809935 |
| 3 | 0.25Ec | 0.61 | 0.97 | 0.91 | 0.90 | 0.698 | 0.69810232 | 0.69810025 |
| 4 | 0.5Ec | 0.32 | 0.66 | 0.60 | 0.61 | 0.698 | 0.69809688 | 0.6980982 |
| 5 | 1.0Ec | -0.01 | 0.32 | 0.28 | 0.31 | 0.698 | 0.69809688 | 0.6980982 |
| 6 | 2.0Ec | -0.31 | 0.02 | -0.02 | 0.02 | 0.698 | 0.69809688 | 0.6980978 |
| 7 | 3.0Ec | -0.45 | -0.14 | -0.12 | -0.19 | 0.698 | 0.69810232 | 0.6981013 |
| 8 | 4.0Ec | -0.66 | -0.24 | -0.27 | -0.31 | 0.698 | 0.69810776 | 0.698108 |
| 9 | 5.0Ec | -0.71 | -0.35 | -0.39 | -0.39 | 0.698 | 0.69811321 | 0.698111 |
| 10 | 6.0Ec | -0.75 | -0.44 | -0.44 | -0.50 | 0.698 | 0.69808464 | 0.698083 |
| 11 | 7.0Ec | -0.83 | -0.53 | -0.53 | -0.53 | 0.698 | 0.69810097 | 0.698100 |
| 12 | 8.0Ec | -0.92 | -0.59 | -0.60 | -0.55 | 0.698 | 0.69811865 | 0.698116 |
| 13 | 9.0Ec | -0.95 | -0.64 | -0.63 | -0.67 | 0.698 | 0.69810232 | 0.698104 |
| 14 | 10.0Ec | -0.97 | -0.67 | -0.70 | -0.72 | -- | -- | -- |
Tables 3 and 4
show the recovered periods
![]() from the multichannel PDM
for the first and the second groups of simulations, respectively.
As a noise level indicator, we define
a logarithmic signal to noise ratio as
from the multichannel PDM
for the first and the second groups of simulations, respectively.
As a noise level indicator, we define
a logarithmic signal to noise ratio as
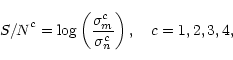 |
(27) |
 |
Figure 4: Detection levels in the PDM search for the second group of simulations. For details, see Fig. 3 |
 |
Figure 6: Set of PDM spectra computed for the single channels and for the combined multichannel of set 12 (noise level 8.0 Ec) in the second group of simulations |
In Figs. 3 and 4, these results are depicted graphically. We can see the clear difference between detection levels for the PDM search. The main peak in the spectra for the U, B, V and R channels "sinks'' into the noise significantly earlier than the main peak in the combined spectrum. As an illustration, we depict some actual spectra in Figs. 5 and 6. Here, it needs to be remarked that the deepest minimum at 0.698 in the (V) spectrum of Fig. 6 was produced accidentally by random fluctuations in the data set 12. In the second group of simulations, the V channel has already stopped working from the set 7 (Fig. 4), for which Fig. 5 shows its last correctly working spectrum.
Our simple tests with the restricted period search range well demonstrate that the expected improvement in precision and in period detection capability indeed takes place.
For a wider search range this nice picture is spoilt by
spurious periods. We applied PDM for the range of periods
![]() and
and
![]() to obtain the single
channel and the combined
spectra
which are depicted
in Fig. 7. All five
spectra show
the four most significant minima at periods 0.349, 0.537, 1.161 and 0.698.
The correct period P=0.698 is always detected but it is far from the
best one! If we look at the corresponding data window which is
computed as in Deeming (1975), we see that
our data spacing is nearly periodic with
to obtain the single
channel and the combined
spectra
which are depicted
in Fig. 7. All five
spectra show
the four most significant minima at periods 0.349, 0.537, 1.161 and 0.698.
The correct period P=0.698 is always detected but it is far from the
best one! If we look at the corresponding data window which is
computed as in Deeming (1975), we see that
our data spacing is nearly periodic with
![]() and
consequently every peak in the spectrum
is echoed multiple times.
Using Eq. (19), we can identify spurious periods
which are actually echoes of the real period. We summarize the results
of the identification of all the nine spurious periods shown in
Fig. 7 in Table 5.
and
consequently every peak in the spectrum
is echoed multiple times.
Using Eq. (19), we can identify spurious periods
which are actually echoes of the real period. We summarize the results
of the identification of all the nine spurious periods shown in
Fig. 7 in Table 5.
| No. |
|
Pr,l,s | (r,l,s) |
| 1 | 0.3490423 | 0.3490497 | (1, 2, 0) |
| 2 | 0.5365817 | 0.5369987 | (1, 2, -1) |
| 3 | 1.1614638 | 1.1634916 | (1, 2, -2) |
| 5 | 1.0733655 | 1.0739974 | (2, 2, -1) |
| 6 | 0.5169787 | 0.5171110 | (2, 2, 1) |
| 7 | 0.8743941 | 0.8726323 | (1, -2, 4) |
| 8 | 0.4107931 | 0.4106471 | (1, 1, 1) |
| 9 | 1.7493248 | 1.7452646 | (1, -1, 2) |
| 10 | 0.4662043 | 0.4654024 | (1, -2, 5) |
 |
Figure 7: PDM spectra of set 5 (noise level 1.0Ec) in the second group of simulations. In all five spectra the real period is fourth ranked according to the depth of a peak. All others are spurious and can be identified according to Eq. (19) |
The spurious period of 0.349 with the deepest minimum occurs at the location where P1, 2, 0 = 0.34904965; the spurious period 0.537 with the second deepest minimum occurs at the location where P1, 2, -1 = 0.53699869 and finally the spurious period of 1.161 with the third deepest minimum occurs at P1, 2, -2 = 1.1634916. Because the amplitudes of the second sinusoidal function is much larger than those of the first one in the simulated model (Table 2), the model curve resembles that of only one sinusoidal function with half the correct period. Thus, this results in the large significance of the first three spurious periods and also for P2,2,-1 and P2,2,1which occur due to fitting with only the (r = 2) sinusoidal function (see explanation in Sect. 2.4).
This is a very important observation. The interplay of the real periodicity with a periodicity in the time point distribution can totally change the general appearance of the spectra. Even when we use all available information (as in the case of the multichannel search), the spurious periods can still complicate our analysis. Paradoxically enough, the improved detection capability of multichannel methods increases also the ability to detect spurious periods. So, when working with real data we must always carefully inspect the spectra using the information from the corresponding data windows to reveal the real periods.
In the last two columns of Tables 3 and 4 the refined periods obtained with LM and NLM are given. Figures 8 and 9 show the final refined periods computed with MPA for the two groups of simulations. For comparison, the results from the search using the best single channel (with highest S/N) are also given (if available). We see that MPA gives as a rule more precise estimates for the main period than those from only the best single channel.
Because the differences between standard least squares methods for the single channels and for the multichannel are minimal, we are not going here into the details of computation. There are only two important additional considerations to be taken into account. The first one is the correct choice of the frequency step for the LM and the correct frequency bracketing for the final NLM refinement. Because of the improved detection capability of the multichannel method, we can in principle choose somewhat larger step sizes for LM and somewhat narrower brackets for a final period improvement. This is certainly true for exact periodicities. But in real life situations, the periods can be slightly varying and, as a result of this, the minima around the periods can have less regular profiles.
 |
Figure 9: Multi and single channel search results for the second group of simulations. See detailed explanations in Fig. 8 |
The second consideration is the error estimation for the final computed periods. In the ideal case of exact periods with reasonably even sampling and full time coverage, the error estimates based on the curvature of WRSS(P) can give good estimates for period errors. But for more complex cases, bootstrap type procedures must be involved (see Jetsu & Pelt 1999). The bootstrap for multichannel methods must take into account the special structure of the input data and will only work if the residuals are uncorrelated. It is reasonable to reshuffle residuals for each channel separately with correct reweighting to ensure that the statistical structure of each bootstrap run will be analogous to the original data.
Copyright The European Southern Observatory (ESO)