2 Methods

A time series of photometric observations can be given as

$$y^c(t_{i}), \ \ \sigma^c(t_{i}), \ \ c = 1, 2,..., C, \ \ i = 1, 2,..., N.$$ (1)

y^c(t_i) is the observed value of the i-th point in the channel c, $\sigma^c(t_{i})$ is its given error, N is the total number of observations and C is the number of channels. The statistical weights w^c_i can be computed from the errors as

w^c_i = $$\frac{1}{\sigma^c(t_i)^2}\cdot$$

Missing points (from some channels) can be properly accounted for by using zero statistical weights.

  
2.1 Multichannel PDM

An ideal method for a preliminary period search should be independent on any assumptions about the exact shape of the light curves and the value of the periods, and be able to detect existing periods on any time scale. The multichannel PDM is devised to achieve this.

For any two observations y^c(t_i) and y^c(t_j), their time difference t_ij, the corresponding weight w^c_ij and the dispersion contribution y^c_ij are

t_ij = | t_i - t_j |, (2)

$$\frac{1}{\sigma^c(t_i)^2 + \sigma^c(t_j)^2} = \frac{w^c_{i} \cdot w^c_{j}}{w^c_{i} + w^c_{j}},$$ w^c_ij = (3)

 

$$w^c_{ij} \cdot \vert y^c_{i} - y^c_{j} \vert^{2}.$$ y^c_ij = (4)

Here, for some time points t_i, the observations y^c(t_i) may not exist for all channels. Thus, the corresponding dispersion contributions and weights are set to zero.

For a real period, a correlation exists between the proximity of the phases of two observations and the proximity of the observed values y^c. For an arbitrarily chosen period P this correlation is much less probable.

The phase dispersion D(P) can discriminate between these two cases:

$$D(P) = \frac{ \sum_{c=1}^C \sum_{i=1}^{N-1} \sum_{j=i+1}^{N}... ...^{N-1} \sum_{j=i+1}^{N} g(t_{ij},P)L(t_{ij})w^c_{ij} }\cdot$$ (5)

Here, note that y^c_ij has already the weights included according to Eq. (4). D(P) is the total weighted and normalized sum of all dispersion contributions for all pairs of observations over all the channels for a trial period P; the additional weight component g(t_ij,P) measures the proximity of the two observations in the phase-process diagram (PPD) computed with the trial period P; L(t_ij) allows us to exclude those pairs of observations which are too far from or too near to each other in time (see below).

Our particular choice for g(t_ij,P) is

 

$$g(t_{ij},P) = \left \{ \begin{array}{ll} 1, & \phi_{ij}(P) \leq \... ...r} \\ & \phi_{ij}(P) > 1-\tau \\ 0, & {\rm otherwise}. \\ \end{array}\right.$$ (6)

where the relative phases $\phi_{ij}$ are defined as

$$\phi_{ij}(P)={\rm Frac}\frac{t_i-t_j}{P}\cdot$$ (7)

The small fixed value $\tau > 0$ determines the maximum distance in phase by which t_i and t_j can be paired for computing D(P). The smaller the value of $\tau$, the lower the number of pairs taken into account. If we compare the PDM with the standard Fourier analysis we can consider our PDM spectrum with $\tau = 0.25$ as a relatively good approximation to the standard power spectrum (with another scaling). Thus, it will be most suitable for detecting single harmonics in the light curve, for which the minima in D(P) correspond to the maxima in the standard power spectrum.

However, reducing $\tau$ enables us to detect more complex waveforms. At the same time, the total number of pairs taken into account in the dispersion estimate decreases and D(P) becomes more erratic. Thus, the value of $\tau$ is somewhat restricted by the amount of available data points.

The selection criterion L(t_ij) is introduced for pairing t_i and t_j according to their distance in time. L(t_ij) is defined as

 

$$L(t_{ij}) = \left \{ \begin{array}{ll} 1, & D_{\rm min} \leq \ver... ...{i} - t_{j}\vert < D_{\rm max} \\ 0, & {\rm otherwise}. \\ \end{array}\right.$$ (8)

The degree of smoothness of the D(P) spectrum obtained by the use of L(t_ij) depends on $D_{\rm max}$. When $D_{\rm max} = t_N - t_1$, all pairs are taken into account when computing D(P), and the maximal resolution is attained. For a smaller value of $D_{\rm max}$, only a subset of pairs is considered and the computed D(P) is smoother. This allows us to compute rough PDM spectra with a larger step in frequency. For long data sets the computing time advantage can be significant. A typical choice of $D_{\rm max}$ depends on the maximum trial period $P_{\rm max}$, e.g. $D_{\rm max} \ge 10 \cdot P_{\rm max}$. It also depends on the actual distribution of the time points.

If the time points t_i and t_j are too close, i.e. |t_i-t_j| is less than the minimal trial period $P_{\rm min}$, the corresponding terms in D(P) do not change significantly for all trial periods so that it does not help to discriminate between them. To avoid unnecessary computations, the lower limit $D_{\rm min}$ discards such pairs from the sum of D(P). A typical choice of $D_{\rm min}$ depends on the minimum trial period $P_{\rm min}$, e.g.  $D_{\rm min} = 0.9 \cdot P_{\rm min}$.

The straightforward computation of the D(P) spectra can be very time consuming. Following a simple binning scheme allows us to speed up calculations significantly.

We divide the full range of $D_{\rm min} \leq t_{ij} < D_{\rm max}$ into

$$K = {\rm Int}\left(\frac{D_{\rm max} - D_{\rm min}}{\Delta}\right) + 1$$ (9)

bins of equal width $\Delta$ (K $\ll$ N for a large data set). The bin width can be chosen as $\Delta = 0.1 \times P_{\rm min}$. Then, we denote the n_q values of t_ij, w_ij^c and y_ij^c in the q-th bin as t_q,k, w_q,k^c and y_q,k^c and derive

$$\bar{t}_q \frac{ \sum_{k=1}^{n_q} t_{q,k} }{ n_q } \ ,$$ = (10)

$$\bar{y}_q^c \sum_{k=1}^{n_q} y_{q,k}^c \ ,$$ = (11)

$$\bar{w}_q^c \sum_{k=1}^{n_q} w_{q,k}^c \ .$$ = (12)

Note that y_q,k^c has already been weighted according to Eq. (4). It is important that these sums do not depend on the trial periods and consequently can be precomputed. The final modified sum for D(P) over all channels is

$$\bar{D}(P) = \frac { \sum_{c=1}^C \sum_{q=1}^{K} g(\bar{t}_q,P)\bar{y}_q^c } { \sum_{c=1}^C \sum_{q=1}^{K} g(\bar{t}_q,P)\bar{w}_q^c } \ ,$$ (13)

and it can be computed reasonably fast even for quite large data sets.

In this first search stage we only identify a set of approximate period candidates for further refinement and identification. Small approximation errors which result from the binning scheme do not hide significant peaks in the PDM spectra. The PDM stage is most useful in the situations where the full time span of the data set is large compared with expected period. For short data sets it can be skipped altogether.

  
2.2 Multichannel linear modeling

In the second stage of the period search we build regular search grids around every period candidate found in the PDM stage. Minima from these short LM spectra with the full resolution are then used as starting values for the nonlinear full precision fit.

We compute the second stage LM spectra using a weighted least squares fit of the model curve $M(t,\beta(P))$ in the form of trigonometric sums (Koen 1999):

 

$${ M( t, \beta(P) ) }$$

$$= A_0 + \sum_{r=1}^R [ A_r\cos(2 \pi r f t) + B_r\sin(2 \pi r f t) ] \ ,$$ (14)

where $f=\frac{1}{P}$ is the trial frequency and $\beta(P)$ includes all linear parameters A₀, A_r, B_r. We choose the order R for the trigonometric polynomial according to $\tau$ chosen in the PDM search. A general relation is $4R\tau = 1$, e.g. R = 1 for $\tau = 0.25$, R = 2 if $\tau = 0.125$, etc. Note that the choice of $\tau$ depends on the complexity of the real light curve and the number of data points, thus, the choices of R and $\tau$ should be consistent.

The step size for the frequency grids is computed from

 

$$\Delta f_{\rm LM} = \frac{1}{ G \cdot (t_{\rm max} - t_{\rm min}) },$$ (15)

where G is a scaling factor which depends on the order of the fit. LM spectra for single harmonic models can be computed on coarser grids. From theory we know (using the Nyquist criterion) that G=2 is good enough, however, to be on the safe side, we normally can use modest oversampling ( $G = 2.5 \cdot 2 = 5$). For higher order trigonometric fits the Nyquist criterion must be applied for the highest frequency in the model and correspondingly the choice $G = 2.5 \cdot 2 \cdot R$ is a good choice.

The last important parameter of the grid search is the frequency range. For every candidate period $P_{\rm PDM} = \frac{1}{f_{\rm PDM}}$, we define a frequency grid around it spanning at least $[ f_{\rm PDM} - 5 \Delta f_{\rm PDM}, f_{\rm PDM} + 5 \Delta f_{\rm PDM} ]$, where $\Delta f_{\rm PDM}$ is the step size in the PDM search. In this way the approximate periods (frequencies) from the first search stage are allowed to contain rather large errors. Relatively wide ranges for the second stage search are important also in situations where multiple, narrowly spaced peaks blend into one in smooth spectra.

The weighted residual sums of squares of a single channel

 

$$WRSS^c(P) = \sum_{i=1}^{N}w^c_i [y^c_i - M( t_i, \beta^c(P) )]^{2},$$ (16)

are combined into

 

$$WRSS(P) = \sum_{c=1}^{C} WRSS^c(P),$$ (17)

to get short spectra around each candidate period. The period values which correspond to the most significant peaks in these spectra form a set of period candidates for a final refinement.

  
2.3 Multichannel nonlinear modeling and error estimation

The precision of the periods obtained from the grid search is limited by the frequency step used. In the third stage we allow trial frequencies to vary continuously, while seeking the minimum of WRSS (Eq. (17)). Here, the period P is treated as the single nonlinear parameter, which determines (through linear weighted least squares estimations) the entire group of parameters $\beta(P)$ (see Eq. (14)). The well-known Brent minimization algorithm (Brent 1973; Chapter 10 in Press et al. 1994) can now be used to find the local minimum of WRSS(P). For each trial frequency we need to choose proper brackets for the minimization. To do that, we must carefully inspect LM spectra obtained in the second stage of the search. However, in most cases the rule of thumb "five steps left, five steps right'' works reasonably well.

As a result of weighted linear least squares fit (for a particular frequency) we get the values and the error estimates for the linear parameters $\beta(P)$(Chapter 15 in Press et al. 1994). The error estimates are valid only in the case when the frequency is assumed to be accurate, i.e. the correlations between the linear parameters and the period are not taken into account. Koen (1999) has pointed out that these error estimates for the linear parameters are different from those obtained when the errors are estimated together with the frequency error. For the nonlinear parameter P, the error estimate $\sigma_P$ of the final period relies on the curvature of the WRSS(P) hypersurface (Chapter 11 in Bevington 1969), which is

 

$$\sigma_P^{2} = \frac{2}{ \partial^2 \chi^2 / \partial P^2 }\cdot$$ (18)

Here, $\chi^{2}$ is identical to the WRSS in Eq. (17). The error estimate $\sigma_P$ is reasonably correct only if the variation of $\chi^{2}$ with respect to the nonlinear parameter P is independent of the values of all the linear parameters $\beta(P)$ (at least near the minimum) and the observation errors in the different channels are uncorrelated and correctly estimated.

After Brent's algorithm traced the minimum of the WRSS function, the parabolic curve fitted to the last three points of ( P, WRSS(P)) is used for the actual computation of $\sigma_P^{2}$.

  
2.4 Spurious periods

The approximate periodicities in the observing times reveal themselves as a series of spurious periods in the classical power spectra (Deeming 1975) as well as in the PDM spectra (Tanner 1948). The general expression for the spurious periods originating from the interplay of a correct period P with periodicities in the observing times is:

$${r\over P_{r,l,s_1,s_2,\dots,s_K}}={l\over P}+\sum_{k=1}^K {s_k\over \delta_k},$$ (19)

where integers $r = 1, 2, \dots, R$, $l = 0, \pm 1, \pm 2, \dots$, $s_k = 0, \pm 1, \pm 2, \dots$, $k = 1, 2, \dots, K$are constrained by the condition $P_{r, l, s_1, s_2, \dots, s_K} > 0$ and the $\delta_k$s are the K periods in the time point spacing. Equation (19) can be derived as follows.

Assume for the moment that the observing times t_i can be exactly expressed as

$$t_i = n_i \cdot \delta_k + t_1,\ \ i=1,2,\dots,N,$$ (20)

where n_i are integer numbers and $\delta_k$ is a particular period in the data spacing. In astronomical observations, the typical periods are the sidereal day, the tropical year and the lunar month. The actual data spacing periods can be found from the transformed data window (see Deeming 1975).

Two observations at times t_i, t_j have the same phase in the PPD when $t_j - t_i = a_{i,j} \cdot P$ for some integer number a_i,j. If these points are from an equally spaced mesh with period $\delta_k$ then for some other integer number b_i,j,k we have $t_j - t_i = b_{i,j,k} \delta_k$. We can now combine the integer numbers a_i,j and b_i,j,k into various integer sums

$$c_{i,j} = l \cdot a_{i,j} + \sum_{k=1}^K s_k \cdot b_{i,j,k},$$ (21)

where l and s_k are arbitrary integer multipliers. Using the above definitions

$$c_{i,j} = {l (t_j - t_i) \over P} + \sum_{k=1}^K {s_k (t_j - t_i) \over \delta_{k}} \ ,$$ (22)

we see that from the closeness of the phases for the correct period Pfollows the closeness of the corresponding phases for a full series of other periods

$$t_j - t_i = P_{l, s_1, s_2, \dots, s_K} \times c_{i,j}$$ (23)

where

$$P_{l, s_1, s_2, \dots, s_K} = \left( {l\over P} + \sum_{k=1}^K {s_k \over \delta_k} \right)^{-1} .$$ (24)

Because all phase dispersion estimates depend on the period through the phases, we can now conclude: if for a certain period P, the PPD shows a small amount of scatter and there is a corresponding peak in the PDM spectrum, then, for all spurious periods $P_{l, s_1, s_2, \dots, s_K}$we can see a similar picture. Because the periodicities in the time point spacings are only approximate, the actual picture is somewhat more complicated. The PPDs for spurious periods tend to have larger scatter when compared with the diagram for the correct period. It is important to note that spurious periods are not artifacts of a certain period search method. They occur universally when there are regularities in the data spacing.

There is an integer index r in Eq. (19) which needs additional explanation. So far, we explained how one particular period P will produce "ghosts'' in the spectra if the data time points contain periodicities. Our simple explanation in terms of phase relations can be complemented by a detailed analysis using Fourier transforms as it is done in Deeming (1975). If we compare PDM spectra (or LM spectra with the order R chosen according to $\tau$) and Fourier spectra, we see that PDM (or LM) spectra, which are computed using multi-harmonic fits, contain many more spurious peaks than the Fourier spectra. Only if we compute PDM (or LM) spectra for a single harmonic model do we get the same picture as in the standard power spectra. The difference comes from the fact that phase-dispersion estimators for one particular trial period Pdepend also on higher harmonics P/r, where $r = 1, 2, \dots$For instance, in the particular case of a two-harmonic LM fit, it is quite obvious that the resulting dispersion for the trial periods depends at least on the spectral power at P and at P/2. This shows up in a quite straightforward way. In the spectrum (computed using a two-harmonic fit), we can see not only the strong minimum for the correct period P(and possibly one at P/2) but also a strong minimum for 2P, which results from the fit of only the second harmonic to the part of the light curve generated by the first harmonic. The PDM (or LM) spectrum detects periods, not harmonics. If the process is periodic with period P, then it is periodic also with period 2P! As a result of this, all spurious periods belonging to every real harmonic in the spectrum will generate additional ghosts around the multiples of periods in the spectra.

Formally we take this into account using the index r in Eq. (19). The set of spurious periods given by Tanner (1948) is the special case for r = 1, K = 1 in Eq. (19). From Eq. (19) we can compute only the positions of potential spurious peaks in the spectrum. The actual strengths of the peaks depend on the harmonic content of the process itself, on the time point distribution etc. (see for instance, the identification of spurious periods of the set 5 from the second group of simulations in Sect. 3). It is also possible that some of the spurious periods can constructively or destructively interfere with each other. This is especially true for multiperiodic light curves (see Pelt 1997).

 

 

Table 1: Model amplitudes and error levels (Eqs. (25, 26)) for the first group of simulations

c	A0c	A1c	B1c	A2c	B2c	Ec
U	0.0	0.9	0.4	0.5	0.4	3.0
B	0.0	0.8	-0.5	0.6	0.3	2.5
V	0.0	-0.7	0.6	0.7	0.2	2.0
R	0.0	-0.6	-0.7	0.8	0.1	1.5

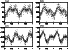Figure 1: PPDs of U, B, V and R of set 3 in the first group of simulations. The noise level is 0.25Ec (see Table 3). The Ecs are fixed for all observations in a particular channel (see Table 1)

 

 

Table 2: Model amplitudes and error levels (Eqs. (25) and (26)) for the second group of simulations

c	A0c	A1c	B1c	A2c	B2c	Ec
U	8.005674	0.011960	0.001157	-0.040586	0.003809	0.030
B	7.960660	0.009258	0.002582	-0.044870	0.006782	0.015
V	7.354608	0.006704	0.002303	-0.042520	0.006269	0.015
R	6.795945	0.006663	0.002186	-0.041944	0.006590	0.015

Figure 2: PPDs of U, B, V and R of sets 7 (left) and 12 (right) in the second group of simulations. The corresponding noise levels are 3.0Ec and 8.0Ec (see Table 4). The Ecs are the real estimated observation errors for UBVR (see Table 2)