The orbital period of RX Hya has been studied by Vyas &
Abhyankar (1989). They collected 6 photoelectric and 55 visual
times of light minimum and pointed out that the O-C curve
showed a cyclic variation with a period of 72.46 years and
an amplitude of
![]() .
By omitting a few visual timings
of earlier epoch, they obtained a rather large increase rate
(
.
By omitting a few visual timings
of earlier epoch, they obtained a rather large increase rate
(
![]() days/year) for the change of
the orbital period. After Vyas and Abhyankar's study, many
times of light minimum have been collected at Eclipsing Minimum
Database. With these timings, the changes in the orbital period
of the system are analyzed. In order to study the variations
in the period of the system, the residuals
days/year) for the change of
the orbital period. After Vyas and Abhyankar's study, many
times of light minimum have been collected at Eclipsing Minimum
Database. With these timings, the changes in the orbital period
of the system are analyzed. In order to study the variations
in the period of the system, the residuals
![]() based
on the following ephemeris:
based
on the following ephemeris:
| (4) |
given in GCVS, are calculated. These
![]() values are listed
in the fifth and ninth columns of Table 3 and shown graphically
against epoch number in Fig. 3. During the calculation, timings
with the same epoch have been averaged and some times of light
minimum listed in Table 3 are the mean values.
values are listed
in the fifth and ninth columns of Table 3 and shown graphically
against epoch number in Fig. 3. During the calculation, timings
with the same epoch have been averaged and some times of light
minimum listed in Table 3 are the mean values.
![\begin{figure}\includegraphics[width=8.8cm]{Fig3.eps}\end{figure}](/articles/aas/full/2000/18/ds9879/Timg18.gif) |
Figure 3: O-C diagram of RX Hydrae. Circles refer to visual and photographic, and dots to photoelectric observations. Also given in solid line is the description of the general trend of the O-C curve |
As displayed in Fig. 3, the orbital period of the system
varies in some complex ways. Since the general trend of the
![]() diagram may show a roughly parabolic distribution
indicating a long-time increase in the orbital period, with the
weight 3 for visual and photographic, and 8 for photoelectric
times of light minimum, a second-order least-squares
solution of the
diagram may show a roughly parabolic distribution
indicating a long-time increase in the orbital period, with the
weight 3 for visual and photographic, and 8 for photoelectric
times of light minimum, a second-order least-squares
solution of the
![]() values yields the following
ephemeris:
values yields the following
ephemeris:
| (5) |
where the coefficient of the square term represents the rate
of change of the period and a continuous period
increase of
![]() days/cycle =
days/cycle =
![]() days/year is calculated which is
equivalent to a period increase of 9.0s/century. The
secular increase only indicates the general trend of the
days/year is calculated which is
equivalent to a period increase of 9.0s/century. The
secular increase only indicates the general trend of the
![]() diagram without describing any particular
characteristics.
diagram without describing any particular
characteristics.
The
![]() residuals from the quadratic ephemeris (5)
are also listed in Table 3 and displayed in Fig. 4. The
residuals from the quadratic ephemeris (5)
are also listed in Table 3 and displayed in Fig. 4. The
![]() values in Fig. 4 clearly show a periodic
oscillation. Most of the observations are photographic
or visual and all the times of light minimum are primary,
this may be caused by the fact that the secondary is
more difficult to observe by such methods. We do not know
whether secondary times of light minimum follow the same
trend of the O-C variation. The circular orbit of RX Hya
(Lucy & Sweeney 1980) suggests that the periodic
oscillation of the
values in Fig. 4 clearly show a periodic
oscillation. Most of the observations are photographic
or visual and all the times of light minimum are primary,
this may be caused by the fact that the secondary is
more difficult to observe by such methods. We do not know
whether secondary times of light minimum follow the same
trend of the O-C variation. The circular orbit of RX Hya
(Lucy & Sweeney 1980) suggests that the periodic
oscillation of the
![]() residuals is not caused
by apsidal motion and that the light-time effect caused by the
presence of a third body may be the real reason. The not
strictly sine-like variation of the
residuals is not caused
by apsidal motion and that the light-time effect caused by the
presence of a third body may be the real reason. The not
strictly sine-like variation of the
![]() curve
suggests that the third body is moving in an elliptical
orbit. The following formula:
curve
suggests that the third body is moving in an elliptical
orbit. The following formula:
![\begin{displaymath}({\rm O{-}C})_{2}=a_{0} +\sum_{i=1}^{2}{[a_{i}\sin(i{\omega}{E})+b_{i}\sin(i{\omega}{E})]}
\end{displaymath}](/articles/aas/full/2000/18/ds9879/img25.gif) |
(6) |
![\begin{figure}\includegraphics[width=8.8cm]{Fig4.eps}\end{figure}](/articles/aas/full/2000/18/ds9879/Timg28.gif) |
Figure 4: O-C residuals of RX Hydrae based on the quadratic ephemeris (5). Solid line is the fit of the third body solution |
From a visual inspection of the trend of these
![]() residuals, it is seen that the orbital eccentricity of the
eclipsing binary around the common centre of the gravity of
the three bodies is small, and the orbital parameters can
be directly determined from the folowing formular (Kopal 1959):
residuals, it is seen that the orbital eccentricity of the
eclipsing binary around the common centre of the gravity of
the three bodies is small, and the orbital parameters can
be directly determined from the folowing formular (Kopal 1959):
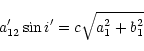 |
(7) |
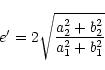 |
(8) |
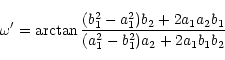 |
(9) |
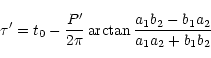 |
(10) |
Copyright The European Southern Observatory (ESO)