To derive the calibration we
used the sample of stars used by
Beers et al. (1999)
for the calibration of the KPindex. For all these stars
UBV photometry and HP2 and KP indices are available.
As calibrators we selected
the stars with low
reddening from Beers et al. (i.e.
![]() ).
To make this criterion more stringent and thus to select a sample
of truly unreddened stars,
we searched
the
Hauck & Mermilliod (1998)
).
To make this criterion more stringent and thus to select a sample
of truly unreddened stars,
we searched
the
Hauck & Mermilliod (1998)
![]() catalog,
through the interface of
the General Catalog of
Photometric Data (GCPD,
Mermilliod et al. 1996)
to find out stars
of the Beers et al. sample with
catalog,
through the interface of
the General Catalog of
Photometric Data (GCPD,
Mermilliod et al. 1996)
to find out stars
of the Beers et al. sample with ![]() photometry.
We then applied the Schuster & Nissen calibration to these data to
obtain
photometry.
We then applied the Schuster & Nissen calibration to these data to
obtain
![]() .
Our final criterion was
that both the estimate of E(B-V) of Beers et al. and
the one derived from Strömgren photometry were less than or equal to
0.01 mag
.
Our final criterion was
that both the estimate of E(B-V) of Beers et al. and
the one derived from Strömgren photometry were less than or equal to
0.01 mag![]() .
.
| STAR | Typea | [Fe/H] | (b-y) | m1 | c1 | |
| BD +18 |
D | -0.46 | 0.440 | 0.258 | 0.256 | 2.560 |
| CD -24 |
D | -3.70 | 0.317 | 0.039 | 0.301 | 2.596 |
| G8-16 | D | -1.59 | 0.322 | 0.071 | 0.292 | 2.595 |
| G11-36 | D | -0.68 | 0.384 | 0.139 | 0.255 | 2.579 |
| G11-44 | D | -2.07 | 0.334 | 0.054 | 0.263 | 2.597 |
| G11-45 | D | -0.01 | 0.431 | 0.249 | 0.359 | 2.602 |
| G12-21 | D | -1.32 | 0.339 | 0.090 | 0.284 | 2.592 |
| G13-35 | D | -1.63 | 0.331 | 0.060 | 0.285 | 2.594 |
| G14-23 | D | -0.27 | 0.370 | 0.150 | 0.316 | 2.590 |
| G14-26 | D | -0.20 | 0.387 | 0.181 | 0.349 | 2.590 |
| G15-6 | D | -0.65 | 0.436 | 0.210 | 0.253 | 2.561 |
| G15-17 | D | -0.39 | 0.475 | 0.315 | 0.246 | 2.553 |
| G17-21 | D | -0.66 | 0.367 | 0.125 | 0.306 | 2.588 |
| G17-30 | D | -0.48 | 0.396 | 0.164 | 0.303 | 2.574 |
| G24-15 | D | -1.10 | 0.342 | 0.092 | 0.273 | 2.597 |
| G37-26 | D | -1.93 | 0.351 | 0.058 | 0.208 | 2.584 |
| G44-6 | D | -0.54 | 0.397 | 0.160 | 0.259 | 2.566 |
| G44-30 | D | -0.89 | 0.427 | 0.177 | 0.200 | 2.557 |
| G54-21 | D | -0.03 | 0.387 | 0.195 | 0.319 | 2.602 |
| G57-11 | D | 0.03 | 0.412 | 0.230 | 0.328 | 2.593 |
| G58-23 | D | -0.97 | 0.407 | 0.138 | 0.219 | 2.565 |
| G58-25 | D | -1.41 | 0.344 | 0.079 | 0.258 | 2.589 |
| G58-41 | D | -0.33 | 0.371 | 0.150 | 0.344 | 2.591 |
| G59-1 | D | -1.02 | 0.424 | 0.186 | 0.204 | 2.567 |
| G59-24 | D | -2.42 | 0.332 | 0.054 | 0.225 | 2.593 |
| G60-48 | D | -1.63 | 0.365 | 0.074 | 0.189 | 2.583 |
| G62-44 | D | -0.58 | 0.473 | 0.295 | 0.248 | 2.554 |
| G62-52 | D | -1.28 | 0.430 | 0.167 | 0.190 | 2.553 |
| G63-46 | D | -0.91 | 0.382 | 0.139 | 0.283 | 2.584 |
| G65-47 | D | -0.35 | 0.405 | 0.188 | 0.281 | 2.584 |
| G66-15 | D | -0.20 | 0.405 | 0.204 | 0.319 | 2.582 |
| G80-15 | D | -0.78 | 0.365 | 0.126 | 0.272 | 2.586 |
| G88-32 | D | -2.36 | 0.309 | 0.051 | 0.357 | 2.591 |
| G97-43 | D | -0.49 | 0.463 | 0.256 | 0.277 | 2.554 |
| G113-24 | D | -0.49 | 0.383 | 0.146 | 0.301 | 2.588 |
| G114-26 | D | -1.78 | 0.349 | 0.076 | 0.250 | 2.594 |
| G119-64 | D | -1.42 | 0.319 | 0.073 | 0.319 | 2.600 |
| G121-12 | D | -0.92 | 0.350 | 0.094 | 0.287 | 2.592 |
| G160-3 | D | -0.14 | 0.414 | 0.217 | 0.339 | 2.584 |
| G162-16 | D | -0.53 | 0.396 | 0.167 | 0.323 | 2.586 |
| G162-51 | D | -0.52 | 0.377 | 0.145 | 0.305 | 2.583 |
| G162-68 | D | -0.54 | 0.425 | 0.202 | 0.206 | 2.565 |
| G165-39 | D | -2.05 | 0.309 | 0.055 | 0.354 | 2.602 |
| G200-62 | D | -0.45 | 0.479 | 0.304 | 0.273 | 2.552 |
| G229-34 | D | -0.50 | 0.403 | 0.190 | 0.334 | 2.579 |
| G271-34 | D | -0.68 | 0.386 | 0.155 | 0.262 | 2.576 |
| HD 693 | TO | -0.38 | 0.328 | 0.130 | 0.405 | 2.621 |
| HD 3567 | SG | -1.29 | 0.328 | 0.089 | 0.330 | 2.600 |
| HD 6461 | G | -0.93 | 0.500 | 0.199 | 0.434 | 2.554 |
| HD 16031 | D | -1.71 | 0.323 | 0.069 | 0.302 | 2.606 |
| HD 20010 | SG | -0.27 | 0.339 | 0.156 | 0.411 | 2.624 |
| HD 34328 | D | -1.61 | 0.365 | 0.063 | 0.205 | 2.569 |
| HD 76932 | D | -0.99 | 0.359 | 0.119 | 0.298 | 2.584 |
| HD 90508 | D | -0.23 | 0.397 | 0.175 | 0.298 | 2.578 |
| HD 105590 | HB | -0.17 | 0.414 | 0.229 | 0.321 | 2.591 |
| HD 113083 | D | -1.04 | 0.367 | 0.122 | 0.254 | 2.587 |
| HD 114762 | D | -0.70 | 0.365 | 0.125 | 0.297 | 2.588 |
| HD 134169 | SG | -0.85 | 0.370 | 0.119 | 0.312 | 2.582 |
| HD 184499 | D | -0.58 | 0.390 | 0.143 | 0.314 | 2.578 |
| HD 193901 | D | -1.08 | 0.381 | 0.103 | 0.217 | 2.573 |
| HD 200580 | D | -0.75 | 0.364 | 0.149 | 0.305 | 2.599 |
| HD 201889 | D | -0.92 | 0.388 | 0.148 | 0.281 | 2.577 |
| HD 201891 | D | -1.13 | 0.358 | 0.104 | 0.262 | 2.590 |
| HD 205156 | D | -0.57 | 0.398 | 0.161 | 0.256 | 2.573 |
| HD 219617 | D | -1.31 | 0.344 | 0.078 | 0.246 | 2.597 |
Out of the sample of
Beers et al. (1999)
65 stars satisfy our criterion
and they are reported in Table 1, the star name is given in Col. (1),
Col. (2) gives the star type, according to
Beers et al. (1999).
Column (3) is [Fe/H] and Cols. (4)-(7) provide the Strömgren
photometry extracted from the
Hauck & Mermilliod (1998)
catalogue.
We performed a ![]() fit
on this sample of stars for several functional forms. We
computed the rms of the fit and we then discarded
those stars whose residual was greater than
fit
on this sample of stars for several functional forms. We
computed the rms of the fit and we then discarded
those stars whose residual was greater than
![]() rms.
This was aimed at further cleaning the sample by rejecting
stars which are either
reddened or whose colours or line indices are affected by
larger errors. Quite interesting only one star,
CD
rms.
This was aimed at further cleaning the sample by rejecting
stars which are either
reddened or whose colours or line indices are affected by
larger errors. Quite interesting only one star,
CD
![]() 17504, was discarded,
whichever functional form was used.
This star is also the most metal-poor of the sample, in fact
the only one below
17504, was discarded,
whichever functional form was used.
This star is also the most metal-poor of the sample, in fact
the only one below
![]() .
Thus our fits were all
performed on a sample totalling 64 stars.
.
Thus our fits were all
performed on a sample totalling 64 stars.
We began with the assumption that both (B-V) and HP2strongly depend on temperature; we therefore fit a linear relation
| param. | error | |
| x1 | 0.5734 | 0.0004 |
| x2 | -0.2759 | 0.0006 |
| x3 | 0.1040 | 0.0003 |
| x4 | 0.2676 | 0.0006 |
The rms of the fit was 0.0153 mag and
![]() ,
i.e.
,
i.e.
![]() ,
which indicates a good fit.
In Fig. 1, panel a) we show a plot of (B-V)versus the right hand side of Eq. (1).
Panels b) and c) display the residuals as a function
of metallicity and (B-V) colour, respectively.
,
which indicates a good fit.
In Fig. 1, panel a) we show a plot of (B-V)versus the right hand side of Eq. (1).
Panels b) and c) display the residuals as a function
of metallicity and (B-V) colour, respectively.
The range of validity of the calibration is
fixed by the properties of the calibrator stars. In our case
these are:
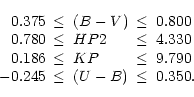
![\begin{figure}
\includegraphics[width=17cm,clip]{figfit.eps}\end{figure}](/articles/aas/full/2000/15/ds9887/Timg46.gif) |
Figure 1:
a) The right hand side of Eq. (1) for the calibrators as a function of (B-V).
The star CD
|
A matter of concern is wether the luminosity (gravity) dependence
of the calibration is properly captured by the (U-B) colour.
Inspection of Table 1 reveals that, although we did not impose
any selection criterion on luminosity, most of our stars are dwarfs,
only one is a giant, three sub-giants and one horizontal branch.
This is a result of imposing a very tight criterion on reddening
for the calibrators:
all low-reddening stars are nearby and therefore most are dwarfs.
So formally our calibration is valid only for dwarfs.
In Fig. 2 we show the residuals of the fit
as a box plot in the
![]() plane.
There appears to be no obvious trend of the residuals with the
luminosity of the stars, we may therefore expect that
the calibration is in fact equally applicable to dwarfs and
giants, as is the Schuster & Nissen calibration.
plane.
There appears to be no obvious trend of the residuals with the
luminosity of the stars, we may therefore expect that
the calibration is in fact equally applicable to dwarfs and
giants, as is the Schuster & Nissen calibration.
Copyright The European Southern Observatory (ESO)