

Up: Dredge-up effects in galactic nebulae
Subsections
Observations were performed using telescopes at ESO (1.52 m) and at
Laboratório Nacional de Astrofísica (LNA), Brazil (1.60 m).
At ESO a Boller & Chivens Cassegrain spectrograph was used with a
Loral/Lesser CCD
and grating allowing a reciprocal dispersion of about 2.5 Å/pixel.
At LNA, a Boller & Chivens Cassegrain spectrograph
was also used with a SITe CCD but with a smaller dispersion, namely,
4.4 Å/pixel. A long east-west slit was used in all observations. The log of
the observations is given in Table 1.
Table 1:
Log of the observations
|
Object |
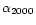 |
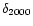 |
Date |
Observatory |
|
SMP 01 |
00 24 05 |
-73 37 22 |
1999 Aug. 19 |
ESO |
| SMP 02 |
00 32 39 |
-71 41 59 |
1999 Aug. 19 |
ESO |
| SMP 03 |
00 34 21 |
-73 13 24 |
1999 Aug. 19 |
ESO |
| SMP 04 |
00 40 42 |
-75 17 00 |
1999 Aug. 20 |
ESO |
| SMP 05 |
00 41 22 |
-72 45 17 |
1999 Jul. 18 |
LNA |
| SMP 06 |
00 41 28 |
-73 47 07 |
1999 Jul. 18 |
LNA |
| SMP 07 |
00 42 28 |
-73 20 55 |
1999 Aug. 15 |
ESO |
| SMP 08 |
00 43 25 |
-72 38 18 |
1999 Aug. 20 |
ESO |
| SMP 09 |
00 45 21 |
-73 24 00 |
1000 Dec. 28 |
ESO |
| SMP 10 |
00 47 00 |
-72 49 16 |
1999 Jul. 20 |
LNA |
| SMP 11 |
00 48 36 |
-72 58 00 |
1999 Jul. 20 |
LNA |
| SMP 12 |
00 49 21 |
-73 52 59 |
1999 Aug. 16 |
ESO |
| SMP 13 |
00 49 52 |
-73 44 23 |
1999 Dec. 26 |
ESO |
| SMP 14 |
00 50 35 |
-73 43 00 |
1999 Dec. 27 |
ESO |
| SMP 16 |
00 51 27 |
-72 26 11 |
1999 Dec. 29 |
ESO |
| SMP 17 |
00 51 56 |
-71 24 45 |
1999 Aug. 17 |
ESO |
| SMP 18 |
00 51 58 |
-73 20 32 |
1999 Aug. 17 |
ESO |
| SMP 19 |
00 53 11 |
-72 45 07 |
1999 Aug. 18 |
ESO |
| SMP 21 |
00 56 31 |
-72 27 01 |
1999 Dec. 26 |
ESO |
| SMP 22 |
00 58 37 |
-71 35 49 |
1999 Aug. 17 |
ESO |
| SMP 23 |
00 58 42 |
-72 56 59 |
1999 Aug. 20 |
ESO |
| SMP 25 |
00 59 41 |
-71 38 16 |
1999 Dec. 28 |
ESO |
| N 9 |
00 43 37 |
-73 02 26 |
1999 Aug. 15 |
ESO |
Image reduction and analysis were performed using the IRAF package,
including the classical procedure to reduce long slit spectra:
bias, dark and flat-field corrections, spectral profile extraction,
wavelength and flux calibrations. Atmospheric extinction
was corrected using mean coefficients for each observatory,
and flux calibration was secured by the observation of standard stars (at least
three) every night.
Emission line fluxes were calculated assuming Gaussian
profiles, and a Gaussian de-blending routine when necessary.
A table with
dereddened line intensities is
available in electronic form at CDS. Adopting a scale in which
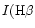 )
= 100, typical errors in the intensities
are of about 15% for lines stronger than 10 and of about 30% for weaker lines.
Interstellar reddening was estimated using
the Balmer ratio H
)
= 100, typical errors in the intensities
are of about 15% for lines stronger than 10 and of about 30% for weaker lines.
Interstellar reddening was estimated using
the Balmer ratio H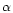 /H
/H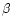 ,
assuming Case B (Osterbrock 1989)
and adopting the extinction law by Cardelli et al. (1989). E(B-V) values derived
for each nebula are given in Table 2.
,
assuming Case B (Osterbrock 1989)
and adopting the extinction law by Cardelli et al. (1989). E(B-V) values derived
for each nebula are given in Table 2.
Electron densities were estimated from the [SII] ratio
 6716/
6716/ 6731 and
from the [ArIV] ratio
6731 and
from the [ArIV] ratio  4711/
4711/ 4740, when the appropriate lines
were available. Electron temperatures were derived from both [OIII]
4740, when the appropriate lines
were available. Electron temperatures were derived from both [OIII]
 4363/
4363/ 5007
and [NII]
5007
and [NII]  5754/
5754/ 6584 line ratios. Whenever these temperatures
were comparable, we have adopted a mean value,
otherwise the [OIII] temperature was used to estimate abundances of higher
ionization potential ions like O+2, S+2, Ar+2,+3, Ne+2
and the [NII]
temperature of lower potential ions like O+, N+, S+.
Temperatures
and densities adopted for each nebula are also listed in Table 2. A compilation
of physical parameters for Magellanic planetaries
was prepared by Richer (1993). A comparison between common objects
indicates that the average temperature difference between literature and our
estimates amounts to 640 K, with a dispersion of 1680 K.
Electron densities have a higher difference
(of about 60% on the average). These differences are probably due to
artifacts. They can be related to
errors in the flux determination of the [SII] lines, frequently weak and
with considerable uncertainties in their fluxes.
Different origins of the atomic data used to derive
densities from the [SII] ratio could also account for this dispersion,
however, it should be emphasized that no
systematic effects were observed between the different samples.
6584 line ratios. Whenever these temperatures
were comparable, we have adopted a mean value,
otherwise the [OIII] temperature was used to estimate abundances of higher
ionization potential ions like O+2, S+2, Ar+2,+3, Ne+2
and the [NII]
temperature of lower potential ions like O+, N+, S+.
Temperatures
and densities adopted for each nebula are also listed in Table 2. A compilation
of physical parameters for Magellanic planetaries
was prepared by Richer (1993). A comparison between common objects
indicates that the average temperature difference between literature and our
estimates amounts to 640 K, with a dispersion of 1680 K.
Electron densities have a higher difference
(of about 60% on the average). These differences are probably due to
artifacts. They can be related to
errors in the flux determination of the [SII] lines, frequently weak and
with considerable uncertainties in their fluxes.
Different origins of the atomic data used to derive
densities from the [SII] ratio could also account for this dispersion,
however, it should be emphasized that no
systematic effects were observed between the different samples.
Table 2:
Electron temperatures and densities
|
Object |
E(B-V) |
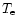 [OIII](K) [OIII](K) |
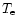 [NII](K) [NII](K) |
 [SII](cm-3) [SII](cm-3) |
 [ArIV](cm-3) [ArIV](cm-3) |
|
SMP 01 |
0.11 |
11900 |
11800 |
47600: |
- |
| SMP 02 |
0.11 |
13700 |
11460 |
4090 |
4270 |
| SMP 03 |
0.04 |
13270 |
- |
- |
21000: |
| SMP 04 |
0.00 |
14980 |
12700: |
- |
4860 |
| SMP 05 |
0.42 |
12400 |
10800 |
4160 |
2300 |
| SMP 06 |
0.23 |
12800 |
9700 |
>3300: |
60000: |
| SMP 07 |
0.09 |
15660 |
9300: |
1140 |
- |
| SMP 08 |
0.02 |
11800 |
10200: |
700 |
3780 |
| SMP 09 |
0.60 |
13470 |
10000: |
770 |
880 |
| SMP 10 |
0.57 |
9800 |
- |
860: |
- |
| SMP 11 |
0.37 |
14000 |
11500: |
1800: |
- |
| SMP 12 |
0.00 |
13800 |
9100: |
880: |
370: |
| SMP 13 |
0.03 |
10800 |
- |
10000 |
- |
| SMP 14 |
0.03 |
11600 |
- |
430 |
500 |
| SMP 16 |
0.02 |
10700 |
- |
3700 |
- |
| SMP 17 |
0.27 |
11230 |
10300 |
3270 |
400 |
| SMP 18 |
0.17 |
12400: |
12100: |
4090 |
- |
| SMP 19 |
0.28 |
11570: |
9780: |
1580 |
2900 |
| SMP 21 |
0.16 |
23500 |
23300: |
8400 |
11220 |
| SMP 22 |
0.24 |
22400 |
10620 |
1550 |
- |
| SMP 23 |
0.00 |
13700 |
11700: |
- |
1210 |
| SMP 25 |
0.00 |
38700 |
- |
3760 |
5390 |
| N 09 |
0.15 |
12700 |
12000 |
170 |
- |
Ionic abundances were calculated for each ion of interest by solving the
statistical
equilibrium equations for a three-level atom model, including radiative and
collisional transitions. Elemental abundances were then derived through ionization
correction factors (icf) adopted to account for unobserved ions of each element.
We used the same icf's adopted in our precedent publications (Costa et al. 1996).
Resulting
abundances are given in Table 3.
Typical errors are about 0.2 dex for O, N,
Ne and 0.3 dex for S and Ar. Helium abundances
deserve further attention, since collisional corrections by Clegg (1987) may
be overestimated up to a factor of two (Peimbert & Torres-Peimbert 1987). Here
we have adopted Clegg's formulae multiplied by an empirical
factor equal to 0.6, since this gives a much better agreement between
He+ abundances derived from the recombination lines HeI 4471, 5876
and 6678. In the case of helium, when three digits are
given, errors are of the order of 0.004 and, when discrepancies between the three
HeI lines are greater than 0.02 the mean value is followed by ":''.
4471, 5876
and 6678. In the case of helium, when three digits are
given, errors are of the order of 0.004 and, when discrepancies between the three
HeI lines are greater than 0.02 the mean value is followed by ":''.
Previous chemical studies of PN in the SMC have shown that
taking the whole sample, the average oxygen
abundance tends to be higher than the mean values
found for type I objects only (see, for instance, Leisy & Dennefeld 1996), a
result not confirmed by the present study, as will be seen later. If some
non-type I objects are misclassified, this could be a possible explanation.
Galactic type I PN, besides the He and N excess, are characterized by their bipolar
morphology, average distance to galactic plane and peculiar
 velocity
(Maciel & Dutra 1992). At the distance of the Clouds, morphologies are not
presently
available and one should wait for future high angular resolution observations,
using large aperture southern telescopes (VLT, Gemini) now becoming
operational.
The Clouds and the Galaxy have different dynamical structures, so the
kinematical
and space distributions are not directly comparable. Thus, for the moment, He
and
N abundances are the only classification criteria. As de Freitas Pacheco et al.
(1993a)
have already emphasized, since the Clouds have lower metallicities, the
self-enrichment
condition to be applied is not necessarily the same as that first defined
by Peimbert
& Torres-Peimbert (1983).
Here we adopted a more conservative position. Since
our main goal is to investigate the reality of the anti-correlation N/O vs. O/H,
we used only He abundance to classify the objects in our sample,
assuming that objects with He/H > 0.11 are genuine type I PN as
indicated in
the last column of Table 3. This is a more drastic limit than that assumed
either by de Freitas
Pacheco et al. (1993a) or by Leisy & Dennefeld (1996), but it gives a higher
confidence
in our analysis. We will return to this point later.
velocity
(Maciel & Dutra 1992). At the distance of the Clouds, morphologies are not
presently
available and one should wait for future high angular resolution observations,
using large aperture southern telescopes (VLT, Gemini) now becoming
operational.
The Clouds and the Galaxy have different dynamical structures, so the
kinematical
and space distributions are not directly comparable. Thus, for the moment, He
and
N abundances are the only classification criteria. As de Freitas Pacheco et al.
(1993a)
have already emphasized, since the Clouds have lower metallicities, the
self-enrichment
condition to be applied is not necessarily the same as that first defined
by Peimbert
& Torres-Peimbert (1983).
Here we adopted a more conservative position. Since
our main goal is to investigate the reality of the anti-correlation N/O vs. O/H,
we used only He abundance to classify the objects in our sample,
assuming that objects with He/H > 0.11 are genuine type I PN as
indicated in
the last column of Table 3. This is a more drastic limit than that assumed
either by de Freitas
Pacheco et al. (1993a) or by Leisy & Dennefeld (1996), but it gives a higher
confidence
in our analysis. We will return to this point later.
Average abundances are shown in Table 4, either for type
I PN as
for all the sample. Objects with uncertain He abundances were excluded when
average
values were computed for type I planetaries. For comparison, average abundances
for HII
regions taken from Dennefeld (1989) are also given, excepting for oxygen, taken
from the HII region sample by Russel & Dopita (1990).
Inspection of Table 4 indicates immediately that no significant differences
exist between average
abundances of type I PN and the ensemble average, although type I seem to have
slightly higher
values. However we should emphasize that we are still playing with small numbers
and a large sample is necessary to draw a more firm conclusion. Nevertheless
our mean values are
quite consistent with interstellar medium abundances and, in particular oxygen.
It is worth mentioning that Hill et al. (1997), from the study of six
K-supergiants, obtained
a mean oxygen abundance
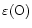 = 8.14
= 8.14 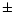 0.12, which agrees both with
PN and HII region average values. A similar behavior is observed for galactic
(de Freitas
Pacheco 1993; Costa et al. 1996) and LMC planetaries (de Freitas Pacheco et al.
1993a).
Taking at face value, these results may be interpreted in the sense that oxygen
was preserved, not being affected by any dredge-up episode.
0.12, which agrees both with
PN and HII region average values. A similar behavior is observed for galactic
(de Freitas
Pacheco 1993; Costa et al. 1996) and LMC planetaries (de Freitas Pacheco et al.
1993a).
Taking at face value, these results may be interpreted in the sense that oxygen
was preserved, not being affected by any dredge-up episode.


Up: Dredge-up effects in galactic nebulae
Copyright The European Southern Observatory (ESO)