2 Resolved spectroscopic binaries

   

Table 1: List of resolved double-lined spectroscopic binaries

HIP	Name	HD	mv1	Sp1	mv2	Sp2	Type	Ref
			(mag)		(mag)
677	$\alpha$ And	358	2.22	B8IV	4.21		SB2	1, 30, 32, 33
2941	ADS 520	3443	5.57	G8V		G8V	LWSB	2, 26, 31, 34
4463	$\eta$ And	5516	4.42	G8III-IV			SB2	3, 35
7580	Kui 7	10009	6.54	F5V	7.77		SB2	4, 36
8903	$\beta$ Ari	11636	2.64	A5V			SB2	5, 64, 65, 67
10064	$\beta$ Tri	13161	3.0	A5III			SB2	6, 45, 62, 63
10644	$\delta$ Tri	13974	4.85	G0V			LWSB	1, 45, 27
10952	$\Sigma$ 248		8.5	K0V	10.5	K0V	SB2	7, 8, 34, 61
12390	$\epsilon$ Cet	16620	4.84	F5V		F6V	LWSB	1, 27, 37
12623	12 Per	16739	4.91	F9V			SB2	1, 26, 37, 59, 60
14328	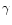$\gamma$ Per	18925	3.25	G8III	4.49	A3V	SB2	9, 10
20087	51 Tau	27176	5.64	A8V		G0V	LWSB	11, 37
20661	Fin 342	27991	6.44	F7V			SB2	12, 37
24608	$\alpha$ Aur	34029	0.08	G8III		G0III	SB2	13, 14, 57, 58
28360	$\beta$ Aur	40183	1.96	A2IV			SB2	1, 45, 56
38382	9 Pup	64096	5.72	G2V	6.17		SB2	1, 2, 27, 37
45170	Fin 347Aa	79096	6.49	G8V		G8V	SB2	15, 37, 49
46404	HR 3750	81809	5.80	G2V	6.60	G9V	LWSB	2, 27, 34, 37
57565	93 Leo	102509	4.60	G8III		A7V	SB2	16, 45
65378	$\zeta^1$ UMa	116656	2.27	A1VpSrSi			SB2	1, 54, 55
71683/1	$\alpha$ Cen	128620/1	-0.01	G2V	1.33	K1V	SB2	1
73182	Gl 570B	131976	8.33	M1.5V	9.94	M3V	LWSB	17, 43
75312	$\eta$ CrB A	137107/8	5.62	G2V	5.96	G2V	LWSB	2, 26, 34
85667	$\Sigma$ 2173	158614	6.02	G9IV-V	5.93	G9IV-V	SB2	1, 18, 26, 34, 37
87895	HR 6697	163840	6.39	G0-2V	9.19	K2-5V	SB2	19
88601	70 Oph	165341	4.2	K0V	6.0	K5V	SB2	20, 34, 51, 52, 53
89937	$\chi$ Dra	170153	3.57	F7V			SB2	1, 26, 37, 66
91636	$\Sigma$ 2367	172865	7.47	G5IV	7.97	G5IV	SB2	21, 22, 34, 50
95995	Gl 762.1	184467	6.59	K1V			SB2	2, 37, 48, 49
96683	$\phi$ Cyg	185734	5.31	K0III	5.6	K0III	SB2	23, 24, 25, 47
98416	Gl 773.3	189340	5.88	F8V			LWSB	1, 37, 46
99376	ADS 13461	191854	8.058	G4V	8.598	G8V	LWSB	26, 34
99473	$\theta$ Aql	191692	3.23	B9.5III			SB2	1, 44, 45
103655	Gl 815AB		10.29	dM3e	12.19		SB3	2, 34, 43
104858	$\delta$ Equ	202275	5.25	F8V	5.25		SB2	2, 27, 37
104987	$\alpha$ Equ	202447/8	3.92	G2III		A5V	SB2	28, 41, 42
108917	$\xi$ Cep A	209790	4.29	A3m			SB2	1, 37, 40
111170	Gl 862.1	213429	6.14	F7V			LWSB	1, 37, 39
111528	ADS 16098	214222	8.4	G0IV			SB2	4, 34, 37, 49
114576	ADS 16591	219018	8.4	G2V	8.6	G4V	SB2	29, 34, 38

Ref. 1: Hoffleit & Jaschek 1982; 2: Gliese 1969; 3: Hummel et al. 1993; 4: Tokovinin 1993; 5: Tomkin & Tran 1987; 6: Cowley et al. 1969; 7: Carney et al. 1994; 8: Torres 1995; 9: Bahng 1958; 10: Griffin et al. 1994; 11: Torres et al. 1997a; 12: Torres et al. 1997b; 13: Rufener 1976; 14: Bagnuolo & Sowell 1989; 15: Mason et al. 1996; 16: Batten et al. 1983; 17: Mariotti et al. 1990; 18: Batten et al. 1991; 19: McAlister et al. 1995; 20: Heintz 1988; 21: Christy & Walker 1969; 22: Stephenson & Sanwal 1969; 23: Fernie 1969; 24: Fekel 1992; 25: Armstrong et al. 1992; 26: Duquennoy et al. 1991; 27: Duquennoy & Mayor 1988a; 28: Pike 1978; 29: Dommanget & Nys 1982; 30: Pan et al. 1992; 31: Roman 1952; 32: Tomkin et al. 1995; 33: Aikman 1976; 34: Worley & Douglass 1996; 35: Gordon 1946; 36: Hartkopf et al. 1996; 37: Hartkopf et al. 1997; 38: Duquennoy 1987; 39: Duquennoy et al. 1988; 40: Vickers & Scarfe 1976; 41: Rosvick & Scarfe 1991; 42: Armstrong et al. 1992; 43: Duquennoy & Mayor 1988b; 44: Cesco & Struve 1946; 45: Hummel et al. 1995; 46: Duquennoy & Mayor 1991; 47: Rach & Herbig 1961; 48: McClure 1983; 49: Mayor & Udry (Priv. Comm.); 50: Batten et al. 1982; 51: Berman 1932; 52: Batten et al. 1984; 53: Batten & Fletcher 1991; 54: Fehrenbach & Prevot 1961; 55: Hummel et al. 1998; 56: Smith 1948; 57: Hummel et al. 1994; 58: Barlow et al. 1993; 59: Colacevich 1941; 60: Barlow et al. 1998; 61: Prieur et al. 2000; 62: Struve & Pogo 1928; 63: Ebbighausen 1953; 64: Pan et al. 1990; 65: Gorza & Heard 1971; 66: Tomkin et al. 1987; 67: Hilditch et al. 1988.

Table 1 lists the stars identified as VB-SB2. Columns m_v1 and m_v2contain the apparent visual magnitudes of both components. When the second column is blank, it is likely that the first one actually represents the overall visual magnitude of the binary. Columns Sp₁ and Sp₂ give the spectral types of both components. When only one spectrum is given, it is usually the overall system spectrum.

The column "Type'' identifies how the spectra were actually observed and processed. SB2 designates systems whose spectra of both components are clearly differentiable and the radial velocities can be measured without any supplementary assumption. LWSB (Line-Width Spectroscopic Binary; Duquennoy & Mayor (1991)) are systems whose spectra are never individually separated. In order to disentangle them and obtain the two radial velocities, some extra assumptions (e.g., line profiles) were necessary. The orbital parallax of LWSB and, therefore, the derived masses can be very sensitive to the Gaussians used to disentangle the spectra (e.g. HIP 75312). The column "Ref'' gives the references of the magnitudes and spectral types as well as all observations used for the adjustments.

A few systems are not analyzed even if they belong to the VB-SB2 category. The SB2 systems presented by Delfosse et al. (1999) are absent because neither the radial velocities nor the visual observations have been published yet. For the TPI systems (Malbet et al. 1998; Koresko et al. 1998; Boden et al. 1999), the nature of the visual observations is the reason why we disregarded them. Indeed, for the time being, our code cannot simultaneously fit radial velocities and optical interferometric raw data (i.e. visibilities). The reason for disregarding ADS 14396 is different. The way Griffin (1984) disentangled its spectra to obtain the individual radial velocities makes them very related to the visual orbit he used. We cannot therefore use them together with some visual observations and still claim we get bias-free results.

A few systems have already been described in details in previous papers: HIP 7580 (Pourbaix 1998), 14328 (Pourbaix 1999) and 71683/1 (Pourbaix et al. 1999). For all systems, we list the orbital parameters in Table 2. A few of these binaries are described slightly further. (Dis)agreement is always stated on a $3\sigma$ basis. If the two compared values are given with their own uncertainty, the agreement can be partial only whether the standard deviation of one result or the other is used. When the time interval is larger than the orbital period, the adopted periastron epoch is the one within that interval which maximizes the efficiency (Eichhorn 1989; Pourbaix & Eichhorn 1999).

HIP 2941: $M_{\rm A}=1.09\pm0.08$ $M_{\odot}$ and $M_{\rm B}=0.87\pm0.07$ $M_{\odot}$ are relatively close to the solution of Duquennoy & Mayor (1991). Adding some recent still unpublished radial velocities (Mayor & Udry, priv. comm.), we obtain $\varpi=66.0\pm2.2$ mas, $M_{\rm A}=0.94\pm0.088$ $M_{\odot}$ and $M_{\rm B}=0.70\pm0.070$ $M_{\odot}$ which are more consistent with the spectral types (Gliese 1969).

HIP 10644: Although the standard deviations of the orbital parameters are quite small, we are puzzled by the shape of the cross-correlation dip obtained with CORAVEL (Fig. 1 in the paper by Duquennoy & Mayor (1988a)). It suggests that the two profiles overlap almost every time. It is therefore difficult to imagine that precise radial velocities can be extracted for both components. The authors also assumed the orbit to be circular. Although the mass ratio is close to unity, their difference of magnitudes in blue is $2.0\pm0.2$ mag. No information is given in the paper about the potential inconsistency of these two results ( $\kappa\equiv\frac{M_{\rm B}}{M_{\rm A}+M_{\rm B}}\approx0.5$ and $\Delta m\approx2$ mag).

The simultaneous adjustment of the visual and spectroscopic data is a complete nightmare! In addition to the natural correlation between $\omega$ and T due to the nearly circular orbit, there is another strong, -0.996, correlation between i and $\varpi$. Within the confidence interval on the inclination (7$^\circ$-width), $\sin i$ ranges between 0.22 and 0.34. Therefore, a small variation on i implies a large variation on $\varpi$. That is the reason why our results are quite imprecise (and rather unreliable): $\varpi=136\pm30$mas, $M_{\rm A}=0.25\pm0.16$ $M_{\odot}$ and $M_{\rm B}=0.23$ $\pm$ 0.14 $M_{\odot}$. The parallax after Hipparcos (ESA 1997) is $92.2\pm0.84$ mas is consistent neither with our value nor with the estimate of Van Altena et al. (1991).

HIP 12390: This system was previously known as an SB1 (Abt & Levy 1976) with a somewhat uncertain period (Morbey & Griffin 1987). Using CORAVEL, Duquennoy & Mayor (1988a) could measure the spectra of both components and determined an SB2 orbit. As for HIP 10644, the two cross-correlation profiles (even at maximum separation) largely overlap. Using the visual orbit of Finsen (1970) (based on visual interferometric observations), Duquennoy & Mayor derived $\varpi=66\ \pm$ 10 mas (consistent with Gliese 1969), $M_{\rm A}=1.10\ \pm$ 0.21 $M_{\odot}$ and $M_{\rm B}=0.74\pm0.22$ $M_{\odot}$.

Hartkopf et al. (1989) determined a visual orbit based on almost ten years of speckle interferometric measurements. They did not look at the spectroscopic orbit and neither the parallax nor the masses were derived. One can, however, notice that the visual and spectroscopic orbits are not in perfect agreement. The solution of Hartkopf et al. does not agree with Finsen's either. Most of the visual interferometric observations used by Finsen (1970) have overestimated angular separations thus leading to an overestimated orbital parallax.

From the Hipparcos data and some photometric and astrometric assumptions, Martin & Mignard (1998) derived $M_{\rm A}=1.886~\pm~0.171$ $M_{\odot}$ and $M_{\rm B}=0.990~\pm$ 0.092 $M_{\odot}$. Their estimate for the secondary seems rather low for the announced spectral type F6V. Their mass ratio is also discrepant with respect to the spectroscopic one (Mazeh et al. 1992).

The spectroscopic data from Duquennoy & Mayor (1988a) and all speckle interferometric observations (Hartkopf et al. 1997) yield $\varpi=34.9\pm3.9$ mas, $M_{\rm A}=2.39\pm0.74$ $M_{\odot}$ and $M_{\rm B}=1.55\pm0.48$ $M_{\odot}$. That parallax is consistent with the Hipparcos one: $36.99\ \pm$ 1.76 mas.

HIP 20087: This system illustrates once again the improvement of the efficiency (Eichhorn 1989) when spectroscopic data are added to visual ones (Pourbaix & Eichhorn 1999). Eichhorn & Xu (1990) obtained 0.466 for the efficiency of the orbital parameters of the visual orbit. The present solution corresponds to 0.680, thus confirming the weaker correlation between the parameters.

   

Table 2: The semi-major axis of stars marked with * is expressed in seconds of arc instead of mas. $\varpi$ stands for the parallax and $\kappa$ for the fractional mass ( $\kappa =M_{\rm B}/(M_{\rm A}+M_{\rm B})$

HIP	a	i	$\omega$	$\Omega$	e	P	T	V0	$\varpi$	$\kappa$	$M_{\rm A}$	$M_{\rm B}$
	(mas)	($^\circ$)	($^\circ$)	($^\circ$)		(yr)	(Byr)	(km s-1)	(mas)		($M_{\odot}$)	($M_{\odot}$)
677	24.0	105.6	257.4	284.4	0.535	0.26476	1988.5830	-10.0	33.0	0.298	3.8	1.63
$\pm$	0.13	0.23	0.31	0.21	0.0046	0.000012	0.00026	0.32	0.62	0.0065	0.22	0.074
2941	667	77.6	317.	291.8	0.235	25.09	1898.5	18.4	66	0.42	0.94	0.70
$\pm$	7.0	0.44	2.8	0.47	0.0096	0.029	0.17	0.13	2.2	0.016	0.088	0.079
4463	10.4	31.	210.	70.0	0.008	0.31682	1992.86	-10.4	13.1	0.474	2.6	2.3
$\pm$	0.11	1.4	26	2.5	0.0054	0.000015	0.023	0.29	0.7	0.0091	0.35	0.31
7580	324	96.6	251.6	159.6	0.798	28.8	1989.92	47.8	27.	0.45	1.2	0.96
$\pm$	5.4	0.33	0.67	0.73	0.0066	0.77	0.012	0.12	1.0	0.013	0.13	0.071
8903	36.0	47.5	204.9	83.3	0.8801	0.292941	1981.55900	-3.1	57.1	0.338	2.00	1.02
$\pm$	0.16	0.54	0.33	0.27	0.00080	1.9e-06	1.8e-05	0.15	0.70	0.0026	0.053	0.032
10064	8.03	130.0	118.1	245.2	0.433	0.085941	1984.91300	12.3	24.2	0.281	3.5	1.4
$\pm$	0.061	0.52	0.66	0.67	0.0041	5.2e-07	9.1e-05	0.66	0.63	0.0093	0.25	0.1
10644	9.8	163.	171.	37.	0.011	0.027433	1992.812	-6.6	136.	0.470	0.2	0.2
$\pm$	0.13	3.6	29	1.9	0.0055	4.7e-07	0.0022	0.11	30	0.0098	0.16	0.14
10952*	0.94	147.	175.	158.	0.802	318.	1989.2	10.0	17.	0.4	1.1	0.7
$\pm$	0.022	2.3	3.7	3.5	0.0072	17	0.14	0.98	1.4	0.12	0.32	0.26
12390	106.	24.	41.	270.	0.230	2.651	1983.15	15.5	35.	0.39	2.4	1.6
$\pm$	1.5	2.5	3.4	2.8	0.0062	0.0018	0.011	0.19	3.9	0.015	0.74	0.48
12623	53.1	127.0	89.9	49.3	0.663	0.90622	1993.3410	-23.03	41.7	0.468	1.34	1.18
$\pm$	0.66	0.76	0.30	0.57	0.0021	1.2e-05	0.00028	0.042	0.89	0.0013	0.042	0.037
14328	143.9	90.6	169.6	244.2	0.786	14.593	1947.279	3.2	14.7	0.423	2.5	1.86
$\pm$	0.73	0.71	0.71	0.28	0.0038	0.0046	0.0083	0.13	0.19	0.0061	0.1	0.064
20087	132.9	125.5	339.	350.7	0.167	11.35	1977.74	37.86	17.5	0.45	1.9	1.5
$\pm$	0.95	0.73	1.9	0.61	0.0044	0.021	0.056	0.099	0.61	0.017	0.14	0.2
20661	100.	125.	272.	215.	0.716	6.28	1988.714	39.6	21.	0.476	1.4	1.23
$\pm$	3.1	1.6	1.1	1.7	0.0099	0.011	0.0074	0.11	1.1	0.0077	0.1	0.098
24608	56.4	137.2	269.	220.9	0.002	0.284809	1973.98	29.19	75.0	0.487	2.70	2.56
$\pm$	0.11	0.19	26	0.31	0.0011	5.5e-06	0.021	0.074	0.57	0.0029	0.066	0.043
28360	3.38	75.0	319	294.5	0.000	0.010842	1975.	-15.8	40.7	0.499	2.4	2.44
$\pm$	0.046	0.73	-	0.72	0.0075	7.2e-09	-	0.51	0.77	0.0051	0.1	0.073
38382	602.	80.4	73.1	102.9	0.741	22.70	1985.92	-21.3	62.	0.48	0.93	0.9
$\pm$	7.2	0.21	0.4	0.27	0.0070	0.027	0.021	0.16	2.6	0.018	0.082	0.12
45170	115.4	124.1	350.7	317.6	0.433	2.7052	1982.690	49.82	49.4	0.49	0.89	0.85
$\pm$	0.63	0.64	0.81	0.46	0.0034	0.00095	0.0040	0.076	0.62	0.004	0.029	0.026
46404	406.	84.1	172.	150.8	0.25	34.5	1941.6	55.7	28.	0.37	1.7	1.0
$\pm$	5.7	0.7	6.2	0.46	0.012	0.32	0.50	0.19	3	0.042	0.64	0.25
57565	7.33	49.	277.16	320.	0.000	0.196282	1979.	0.5	13.3	0.476	2.2	2.0
$\pm$	0.096	1.2	-	1.1	0.0052	1.6e-06	-	0.21	0.45	0.0067	0.17	0.13
65378	10.0	61.	105.5	106.	0.529	0.056233	1963.15100	-6.3	40.	0.493	2.5	2.5
$\pm$	0.32	1.2	0.79	1.1	0.0052	3.7e-07	7.6e-05	0.38	1.8	0.0041	0.11	0.12
71683/1*	17.59	79.23	231.8	204.82	0.519	79.90	1955.59	-21.87	737.	0.45	1.16	0.97
$\pm$	0.028	0.046	0.15	0.087	0.0013	0.013	0.019	0.054	2.6	0.013	0.031	0.030
73182	133.	110.	311.	18.	0.765	0.8429	1986.3660	28.1	155.	0.420	0.51	0.37
$\pm$	3.9	2.4	1.5	2.6	0.0083	0.00024	0.00082	0.25	6.5	0.0083	0.038	0.023
75312	860.	58.7	219.2	22.9	0.277	41.586	1892.317	-7.41	54.9	0.472	1.19	1.05
$\pm$	3.3	0.16	0.37	0.19	0.0011	0.008	0.031	0.054	0.97	0.0091	0.071	0.05
85667	977.	99.1	148.	332.3	0.168	46.34	1870.0	-77.18	61.	0.481	0.98	0.90
$\pm$	3.3	0.11	1.3	0.13	0.0025	0.021	0.16	0.069	1	0.0085	0.052	0.045

 

Table 2: continued

HIP	a	i	$\omega$	$\Omega$	e	P	T	V0	$\varpi$	$\kappa$	$M_{\rm A}$	$M_{\rm B}$
	(mas)	($^\circ$)	($^\circ$)	($^\circ$)		(yr)	(Byr)	(km s-1)	(mas)		($M_{\odot}$)	($M_{\odot}$)
87895	84.	68.	315.	359.	0.41	2.4143	1989.514	-32.9	37.	0.392	1.2	0.80
$\pm$	3.0	2.4	1.9	1.4	0.011	0.00077	0.009	0.1	1.8	0.0079	0.11	0.055
88601*	4.554	121.16	14.0	302.12	0.4992	88.38	1895.94	-6.87	193.	0.46	0.90	0.78
$\pm$	0.0052	0.078	0.14	0.097	0.00039	0.017	0.017	0.077	4.2	0.013	0.074	0.040
89937	123.	74.8	299.9	50.5	0.414	0.7680	1984.835	31.90	122.	0.416	1.03	0.73
$\pm$	1.2	0.79	0.97	0.60	0.0083	0.00017	0.0015	0.14	2.1	0.0057	0.050	0.024
91636	239.	121.	348.	244.	0.910	92.2	1980.82	17.8	8.4	0.54	1.22	1.47
$\pm$	3.4	1.6	1.7	1.1	0.0020	0.41	0.015	0.50	0.22	0.018	0.086	0.085
95995	86.	144.	356.	243.	0.360	1.3528	1985.271	11.31	59.	0.482	0.8	0.8
$\pm$	1.4	2.4	2.1	1.5	0.0078	0.00072	0.0047	0.099	4.1	0.0050	0.15	0.14
96683	26.9	80.8	34.	251.0	0.542	1.18872	1936.169	5.2	14.2	0.491	2.46	2.39
$\pm$	0.75	0.63	1.3	0.86	0.0063	4.1e-05	0.0017	0.14	0.42	0.0032	0.055	0.045
98416	150.	6.	142.	147.	0.592	4.895	1982.81	30.02	11.	0.45	53.	43.
$\pm$	2.7	20.0	4.3	3.0	0.0094	0.0054	0.031	0.094	38.	0.022	530.	440.
99376	458.	115.3	159.	321.7	0.492	85.2	1970.4	-43.2	18.	0.44	1.2	0.9
$\pm$	4.4	0.42	1	0.52	0.0033	0.12	0.18	0.20	1.0	0.044	0.23	0.17
99473	3.20	142.	211.	95.	0.59	0.046884	1964.1060	-28.0	14.	0.444	3.2	2.5
$\pm$	0.075	3.1	3.3	3.2	0.013	2.9e-07	0.00012	0.52	1.2	0.0053	0.67	0.54
103655	690.	44.	129.	122.	0.72	29.5	1976.88	-33.97	45	0.24	3.	1.0
$\pm$	50	8.9	3.3	6.5	0.014	0.66	0.048	0.095	14	0.057	2.7	0.65
104858	232.	99.0	8.	203.8	0.440	5.703	1981.47	-15.85	55.0	0.484	1.19	1.12
$\pm$	1.8	0.43	1.0	0.29	0.0046	0.0070	0.012	0.074	0.67	0.0043	0.034	0.032
104987	12.0	153.	120.	34.	0.004	0.27056	1990.96	-17.6	18.	0.47	2.3	2.0
$\pm$	0.14	3.1	30	3.8	0.0072	4.5e-05	0.022	0.21	2.0	0.012	0.77	0.66
108917	72.	68.	273.	85.	0.50	2.241	1970.992	-10.7	38.	0.26	1.0	0.36
$\pm$	1.7	1.4	1.1	1.9	0.021	0.0027	0.0092	0.34	2.1	0.017	0.13	0.051
111170	71.6	67.	352.	262.4	0.38	1.7253	1979.330	-9.72	38.	0.353	1.4	0.78
$\pm$	0.76	1.3	1.7	0.55	0.011	0.00097	0.0069	0.097	1.2	0.0098	0.14	0.051
111528	141.	60.	324.	294.	0.36	22.3	1985.2	6.86	13.3	0.487	1.22	1.16
$\pm$	4.5	2.1	2.2	1.8	0.013	0.11	0.10	0.074	0.65	0.0072	0.094	0.091
114576	204.	104.	130.	106.	0.41	29.1	1983.2	34.5	16.7	0.39	1.3	0.84
$\pm$	5.6	2.4	2.1	2.9	0.015	0.21	0.12	0.12	0.71	0.010	0.11	0.066

HIP 46404: Our parallax is quite discrepant with respect to the Hipparcos one: $32.01\pm1.02$. This discrepancy comes from the spectroscopy and, more precisely, from the two sets of radial velocities obtained by Duquennoy & Mayor (1988a) when they disentangled the blended spectra of this system. However, by re-processing the Hipparcos Transit Data, Söderhjelm (1999) has lately revised the "Hipparcos'' parallax down to $29.1\pm1.1$ mas which yields a mass sum of $2.54\pm0.41$ $M_{\odot}$ thus confirming our results.

HIP 73182: This system has all the features that made it a "tough case'' for the Hipparcos reduction teams. The semi-major axis has the same order of magnitude as the parallax. Moreover, the orbital period is close to one year. The consequence is a large confidence interval on the parallax: $133.63\,\pm\, 33.56$ mas. At this level of confidence, the consistency of this parallax with ours is just fortuitous! Söderhjelm (1999) has lately re-processed the Hipparcos Transit Data and derived $\varpi=169.7\pm1.0$ mas and a mass sum of $0.83\pm0.11$ $M_{\odot}$. His "Hipparcos'' parallax and ours do no longer agree although the mass sums are very consistent.

HIP 75312: Our initial parallax was quite discrepant with respect to the Hipparcos one $53.70\pm1.24$ mas. From the Hipparcos data, Söderhjelm (1999) derived $\varpi=53.5\pm0.9$ mas and a mass sum of $2.41\pm0.14$ $M_{\odot}$. Because we strongly believed that the way the CORAVEL data of this LWSB had been disentangled by the Geneva group was responsible for a large part of this discrepancy, we asked S. Udry to slightly tune the input parameters of the disentangling procedure, which he did. With these revised radial velocities (the procedure was applied to all RVs from Geneva), we now obtain: $\varpi=54.9\,\pm \,0.97$ mas, $M_{\rm A}=1.19\pm0.071$ $M_{\odot}$ and $M_{\rm B}=1.05\pm0.050$ $M_{\odot}$.

HIP 89937: Our adjustment yields $M_{\rm A}=1.03$ $\pm$ 0.050 $M_{\odot}$ and $M_{\rm B}=0.73\pm0.024$ $M_{\odot}$. The masses after Tomkin et al. (1987) as well as ours do not correspond well with what one expects for a F7V and a late G-type dwarf and the masses by Breakiron & Gatewood (1974) remain more likely.

HIP 103655: From the visual observations kept at US Naval Observatory and the radial velocities of A and B by Duquennoy & Mayor (1988b), we cannot derive any stable solution. Using the mass ratio of Fekel et al. (1978), we can compute the systemic velocities of Aa-Ab from the radial velocities of the two components. When these new "measurements'' are added to the set of radial velocities, the shape of the objective function (Pourbaix 1998) starts exhibiting some larger variations and, hence, a global minimum neighborhood. Nevertheless, this region remains valueless. We obtain $\varpi=45\pm14$ mas, $M_{\rm A}=3.1\ \pm$ 2.7 $M_{\odot}$ and $M_{\rm B}=1.0\pm0.65$ $M_{\odot}$. The only result we share with Russell & Gatewood (1980) seems to be the period: $29.5\pm0.6$ years.

Our parallax is totally discrepant with respect to the Hipparcos one, $66.21\pm2.54$ mas, the latter being consistent with the result by Russell & Gatewood (1980). Since both the spectroscopic and visual date are of poor quality, it was expected that the Hipparcos observations would improve the visual part. Söderhjelm (1999) has lately obtained a parallax of $66\pm1.8$ mas and a mass sum of $1.38\ \pm$ 0.34 $M_{\odot}$ from the Hipparcos Transit Data.