

Up: Ab initio calculations of
Table 1 lists the known energy levels for Ndiii from MZH
and the Landé g-factors calculated using the Cowan code.
a Energies and term
designations are from Martin et al.(1978); g-factors followed by a colon are
uncertain due to term mixing.
Log(gf) values were computed for all electric dipole transitions with wavelengths in the
range 2000-7000 Å. A total of 9469 lines and associated gf-values exist in our data files.
To present a complete list of the calculations is beyond the scope of this note. Table 2
shows the calculated gf-values, as well as the cancellation factors (CF, see Sect. 4), for the 54
predicted lines arising from the known energy levels after employing the usual selection rules;
the gf-values have been scaled appropriately for the differences between the calculated
wavelengths and the predicted ones.
Fewer than
half of these lines appear in unpublished lists of the strongest laboratory lines of Ndiii
provided by Crosswhite ([1976]), but many of these have been identified in RE-rich
stars like HR465 (Bidelman et al. [1995])
and HD101065 (Cowley et al. [1998], [2000]). Hundreds
of additional strong lines exist in the Crosswhite data, but it is difficult, if not impossible, given the
uncertainties in the calculated energy levels, to unambiguously classify them using our data.
The full set of computed wavelengths, energy levels, and log(gf) values will be released to the Vienna
Atomic Line Database (VALD,
Piskunov et al. [1995]; Kupka et al. [1999]) for
the purpose of computing opacities for heavily line-blanketed stellar model atmospheres where
especially high precision
in the wavelengths is not required and where the f-sum rule for the oscillator strengths mitigates
somewhat the uncertainties in the individual values.
No corrections to the gf-values given in Table 2 for core polarization effects have been
made due to the fact that our current version of the multi-configuration Hartree-Fock-based
code for doing so
(see Vaeck et al. [1992]) will not handle configurations containing
more than two f-electrons.
We do not expect this to be a significant limitation on the accuracy of the data in Table 2 insofar as
it contains no transitions into or out of any levels assigned to
the 4f36p configuration where such effects are most pronounced.
A modified program to permit core polarization corrections to be made in configurations with greater than
two f-electrons has been kindly
made available to us by G. Gaigalas ([1998]) and awaits implimentation.
Based on the calculations, a re-evaluation of the ionization energy for Ndiii
has been carried out following the approach of Sugar & Reader ([1973]). Using the
computed energy for the lowest level of the 4f36s configuration, 30776 cm-1, and
taking 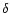 = 455 cm-1 (as found from the formulae of Judd ([1962]) and the
calculated Slater parameter G3(4f36s) = 2125 cm-1), we find the
ionization energy to be 179031
= 455 cm-1 (as found from the formulae of Judd ([1962]) and the
calculated Slater parameter G3(4f36s) = 2125 cm-1), we find the
ionization energy to be 179031 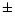 823 cm-1. This result is only 0.2% higher than the
published value, but it reduces the uncertainty by nearly a factor of three over the previous
estimate.
In this determination, we have applied
the Sugar & Reader term value for the center of gravity of the 4f36s configuration
derived from the Rydberg-Ritz formula: T = 147800 cm-1. The uncertainty in the
ionization energy is the
square root of the sum of the squares of the contributing uncertainites. We have adopted the
value given in Sugar & Reader for
823 cm-1. This result is only 0.2% higher than the
published value, but it reduces the uncertainty by nearly a factor of three over the previous
estimate.
In this determination, we have applied
the Sugar & Reader term value for the center of gravity of the 4f36s configuration
derived from the Rydberg-Ritz formula: T = 147800 cm-1. The uncertainty in the
ionization energy is the
square root of the sum of the squares of the contributing uncertainites. We have adopted the
value given in Sugar & Reader for 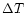 and assumed the error in the energy for the
4f36s 5I
and assumed the error in the energy for the
4f36s 5I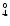 term to be three times the mean deviation in the fitted energies for
the odd parity levels.
term to be three times the mean deviation in the fitted energies for
the odd parity levels.


Up: Ab initio calculations of
Copyright The European Southern Observatory (ESO)