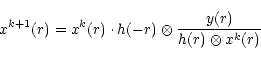3 Image reconstruction

3.1 Deconvolution of the raw image of P Cyg

A deconvolution of the image of P Cyg using 59 Cyg as the PSF has been made using basically the iterative Richardson-Lucy algorithm (RL) ([Richardson 1972]; [Lucy 1974]) to which some improvements have been applied as we shall describe below. To improve the result, a pre-processing of the image was first performed. All images were smoothed using a moving average window of 4$\times$4 pixels. To remove the effects of the coronagraphic mask (clearly visible in Fig. 1 at the right of P Cyg's image), only a central region of 0.9$\times$0.9 arcsec of the smoothed images was conserved. To make the deconvolution procedure faster, the number of points of the images was further reduced by a factor of 16. The resulting images of 32$\times$32 pixels remain correctly sampled (0.028 arcsec compared with the theoretical Shannon limit of 0.044 arcsec for the 1.52 m telescope operated at 656.3 nm).

The RL algorithm was then applied to these pre-processed images using the well-known iterative procedure:

$${x}^{k+1}(r) = {x}^{k}(r) \cdot h(-r) \otimes \frac{ y(r)}{h(r) \otimes {x}^{k}(r)}$$ (1)

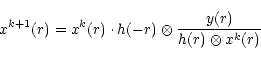where $\otimes$ is the convolution symbol, r denotes the two-dimensional spatial position, y(r) denotes the image of P Cyg, h(r) the image of 59 Cyg taken as the PSF, and where x^k(r) , x^k+1(r) are the reconstructed images at the iteration k and k+1.

Figure 4: Reconstructed image of P Cyg with the RL algorithm stopped at iteration 245. Top: Representation in gray levels in a linear scale. Bottom: Representation in contour plot. Contours levels are not equally spaced and correspond to: 100, 80, 60, 40, 30, 15, 12.5, 9, 6.5, 5, 3.5, 2, 1.2 percent of the image's maximum. North is at the top and East is at the right of the images. This corresponds to a rotation of 104.7$^{\circ }$ clockwise with regards to Fig. 1

To limit the instability that appears in the solution, due to the amplification of noise, we stop the iteration number by using a comparison between the Fourier Transform of the reconstructed object at the iteration k and the Fourier transform of the image reconstructed by a Wiener filter ([Lantéri et al. 1998]; [Lantéri et al. 1999]). The main difficulty is then shifted to a correct determination of the Wiener filter. The comparison led us to choose an iteration number of 245. The result of the deconvolution is given both in grey levels and in a contour plot in Fig. 4. To make the envelope clearly visible, the contour levels are not equally spaced. The general pattern is that of a bright star, not resolved by the 152 cm telescope, surrounded by an extended envelope with bright spots.

These same results were obtained with the reconstruction RL algorithm regularized by a Tikhonov term, and in particular using the Laplacian operator ([Lantéri et al. 1999]). The result of this deconvolution is presented in Fig. 5 for the iteration 250 with a regularization factor equal to 0.01.

Figure 5: Reconstructed image of P Cyg with the RL algorithm regularized by the Laplacian operator. Contours levels are not equally spaced and correspond to: 100, 80, 60, 40, 30, 15, 12.5, 9, 6.5, 5, 3.5, 2, 1.2 percent of the image's maximum. North is at the top and East is at the right of the image

Figure 6: Thick line: Radial profile of the object reconstructed by RL stopped at iteration 245 (image normalized to one). Dashed lines: Gaussian curves. Thin line: Sum of the two Gaussian curves. Intensity is in logarithmic scale

Neglecting the fine structure of the envelope, a normalized circular average of the image centered on the star may be fitted by the sum of two Gaussian curves, of the form: $a {{\rm e}}^{-b \vert r\vert^{2}} + (1-a) {{\rm e}}^{-b' \vert r\vert^{2}}$ where $a~\simeq$ 0.85, $b~\simeq$ 618.2 and $b'~\simeq$ 25.9 if we express r in arcsec. This corresponds to an equivalent width of the envelope of about 0.4 arcsec ( $\frac{2}{\sqrt{b'}}$). The radial curve is shown in a semi-logarithmic scale in Fig. 6. In this model the total integrated flux produced by the envelope (r = (1-a)b/ab') was found to be about 4 times larger than the one produced by the central star. This ratio is not an absolute parameter; it depends of course on the spectral bandwidth of the experiment (Fig. 2).

Figure 7: Representation at the same scale of the reconstructed image of the Fig. 5 (left) and of the PSF (right) in contour plot. The white parts are due to the threshold and the saturation applied to both images: intensities lower than 6% and higher than 15% of the maximum are made white. North is at the top and East is at the right of the images

We may conclude from this first analysis that the envelope of P Cyg is well resolved by the central core of the PSF of the 1.52 m telescope, corrected by the adaptive optics system. However, the envelope remains comparable in size with the residual halo of the PSF. This assumes at least that we are free of anisoplanatism problems ([Fusco et al. 2000]); this absence of variation allows the use of conventional deconvolution methods.

The question then may arise whether some of the fine structures we discovered in this envelope may be due to artifacts of the reconstruction process. A very important issue to consider, is a possible variation of the PSF during the experiment (from P Cyg to 59 Cyg), as discussed recently by Harder and Chelli ([Harder & Chelli 2000]). These authors show that a local non-stationary turbulence may produce strong residual aberrations (clearly visible in the first diffraction ring of their Fig. 17). At worst, we can imagine that the observed structures in our image result only from variations in the PSF, from P Cyg to 59 Cyg.

A comparison between the reconstructed image and the PSF is made in Fig. 7. To make the structures more visible, we used a representation similar to that of Harder and Chelli ([Harder & Chelli 2000]). The images are negatives of intensities and the representation uses threshold and saturation. Doing so, a strong (white) secondary maximum appears in the image of P Cyg, and two lower ones remain far away from the core. Moreover, Fig. 7 shows clear evidence that the central (white) surface of the reconstructed object is larger than that of the PSF (this will be interpreted in the next section as an effect of the envelope). Such a structured image can hardly result from the variations of the PSF. However, it is also difficult to ascertain that our reconstructed image is free of any residual error (much more data would have been necessary for this). To strengthen our confidence in the fine details of the reconstructed image of the envelope, we have implemented a series of tests and processings. They are described in Sects. 3.2 and 3.3, and in the Appendix.

Figure 8: Representations in grey levels of the residual blurred envelope $e(r) \otimes h(r)$ (top) and of the fraction $\gamma h(r)$ of the image of 59 Cyg subtracted from P Cyg (bottom). The sum of these two images gives back the observed image of P Cyg. The orientation is that of Fig. 1

Deconvolution of the envelope - independent of P Cyg

We have further processed the data assuming that P Cyg observed in H$_{\alpha }$ may be fairly represented by an unresolved star surrounded by an extended envelope. Let us write P Cyg as $e(r) + \gamma\delta(r)$, where e(r) is the envelope and $\gamma$ the relative intensity of the star defined by the Dirac function $\delta(r)$. The observed image is then modeled as $y(r) = e(r) \otimes h(r) + \gamma h(r)$. We have implemented a somewhat heuristic procedure that consists of subtracting $\gamma h(r)$ from y(r) to obtain $e(r) \otimes h(r)$. The procedure has some similarity with the CLEAN algorithm ([Högbom 1974]), or the Lucy algorithm ([Lucy 1994]). In practice, it consists of subtracting an appropriate fraction of the image of 59 Cyg correctly shifted from P Cyg. The parameters of this subtraction are determined to leave a smooth pattern for $e(r) \otimes h(r)$, with no remaining bump or hole due to the unresolved star. We found that a fraction $\gamma$ = 20% of the PSF (h(r)), shifted by (X = - 0.3 pixels, Y = +1.3 pixels) was to be subtracted from P Cyg (y(r)). This was done using an interpolation of the images with Mathematica ([Wolfram 1999]). Figure 8 shows the residual blurred envelope $e(r) \otimes h(r)$ (top) and the fraction of the PSF subtracted to the image of P Cyg $\gamma h(r)$ (bottom). This procedure, performed independently of the above deconvolution and parametric estimation of the star plus envelope, led also to the same ratio 4 for the energy of the envelope relative to the central star.

Figure 9: Image reconstruction of the envelope of P Cyg in grey levels (top) and in contour plot (bottom). Contour levels are equally spaced. North is at the top and East is at the right of the images

We then processed the residual blurred envelope $e(r) \otimes h(r)$using the same RL algorithm stopped at the same iteration number 245. The result is depicted both in grey levels and in a contour plot with linear contour spacing in Fig. 9. The image of the envelope is fully consistent with what was obtained in the raw deconvolution of Fig. 4. The bright spots are all found at the same position. Moreover, there is a bright spot very close to the star clearly visible in this representation in the South-West direction; it was only perceptible as a small deformation of the central star in Fig. 4.

3.3 Analysis of the quality of the deconvolution

We have implemented a few more computations to check the quality of the results we give in this paper. The whole deconvolution procedure was also performed using the Image Space Reconstruction Algorithm (ISRA) ([Daube-Witherspoon et al. 1986]) instead of the RL algorithm. The comparison with the image reconstructed by the Wiener filter leads us to the iteration 303. The reconstructed image is presented in Fig. 10.

Figure 10: Reconstructed image of P Cyg with the ISRA algorithm stopped at iteration 303. Contour levels are not equally spaced and correspond to: 100, 80, 60, 40, 30, 15, 12.5, 9, 6.5, 5, 3.5, 2, 1.2 percent of the image's maximum. North is at the top and East is at the right of the image

The two algorithms gave almost the same results, backing up the deconvolution results given in this paper.

In respect to this we may conclude that the deconvolution was carried out taking into account the problem of noise; we also made use of an a priori model, by assuming that P Cyg was the sum of an unresolved star and an envelope. An important question remains: up to what precision can we trust 59 Cyg as an accurate PSF for P Cyg? Several elements enable us to give a positive answer to that question: the seeing conditions were similar for both observations, and we found the same ratio of the flux envelope/star (about 4) before and after deconvolution. It would have been very convincing to have a series of sandwitched observations of P Cyg and a reference, eventually with different seeing conditions, and have all the results that converge towards a unique solution. In fact, we made an elementary test that consisted in dividing the long exposure of P Cyg in two sequences. The same operation was applied to 59 Cyg. We have then made a deconvolution of these four resulting images. The results are very similar to those obtained with the deconvolution presented in Fig. 4 and are not reproduced here. In an alternative we give in the appendix the results of a series of additional tests that tend to confirm 59 Cyg as a correct PSF.

We believe we have interpreted our current data as far as is possible. Of course, future observations, with possibly a larger telescope, will be very useful to confirm our first results and to further specify the morphology of this object.