

Up: Evaluation of Devasthal site
The relationship between the full width at half maximum (FWHM) of a stellar
image point spread function (PSF) formed at the focus of a large telescope and
Fried parameter r0, is given by Dierickx (1992) as
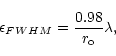 |
(1) |
where 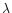 is the
wavelength. The value of
is the
wavelength. The value of
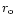 represents the diameter of the telescope for which diffraction
limited image resolution is equal to the FWHM of the seeing limited image
(cf. Fried 1966).
represents the diameter of the telescope for which diffraction
limited image resolution is equal to the FWHM of the seeing limited image
(cf. Fried 1966).
The variance (
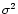 )
of the two
dimensional image position is (cf. Vernin & Muñoz-Tuñón 1995)
given as
)
of the two
dimensional image position is (cf. Vernin & Muñoz-Tuñón 1995)
given as
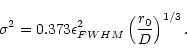 |
(2) |
Thus measuring the image motion at the focus of a telescope of aperture Dand at wavelength 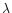 ,
the Fried parameter r0 and hence the seeing
can be deduced from Eq. (1). This technique of measuring image motion
suffers from the erratic motion of the telescope and it is difficult to
separate the image motions due to turbulence and those due to telescope, which
includes wind shaking, guiding and dome effect etc.
The differential image motion monitor (DIMM) measurements eliminate the
effects due to the motion of the telescope and hence enables one to measure
the contributions of the atmosphere to the image degradation. The DIMM
principle is to produce twin images of a star with the same telescope
via two entrance pupils separated by a fixed distance. The assumption that
Kolmogorov turbulence theory accurately describes the effects of
atmosphere upon images, enables us to assess the longitudinal and
transverse (parallel and perpendicular to the aperture alignment) variance
of the differential image motion. The variance of the image motion in the
direction parallel to the line joining the subapertures is given by
(see Sarazin & Roddier 1990)
,
the Fried parameter r0 and hence the seeing
can be deduced from Eq. (1). This technique of measuring image motion
suffers from the erratic motion of the telescope and it is difficult to
separate the image motions due to turbulence and those due to telescope, which
includes wind shaking, guiding and dome effect etc.
The differential image motion monitor (DIMM) measurements eliminate the
effects due to the motion of the telescope and hence enables one to measure
the contributions of the atmosphere to the image degradation. The DIMM
principle is to produce twin images of a star with the same telescope
via two entrance pupils separated by a fixed distance. The assumption that
Kolmogorov turbulence theory accurately describes the effects of
atmosphere upon images, enables us to assess the longitudinal and
transverse (parallel and perpendicular to the aperture alignment) variance
of the differential image motion. The variance of the image motion in the
direction parallel to the line joining the subapertures is given by
(see Sarazin & Roddier 1990)
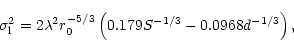 |
(3) |
where S is the diameter of the two entrance pupils and d is the separation between them.
The corresponding expression for the differential image motion perpendicular
to the line joining the two apertures is
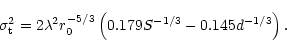 |
(4) |
It should be noted that these relations are valid if S/d 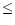 0.5
(Sarazin & Roddier 1990 and references therein). Measuring
0.5
(Sarazin & Roddier 1990 and references therein). Measuring
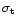 and
and
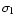 enables us to estimate the respective r0, which when
used in Eq. (1) gives the longitudinal and transverse seeing respectively.
In the present case the value of S/d is 0.15 and 0.21 for 52 cm and 38 cm
telescopes respectively.
enables us to estimate the respective r0, which when
used in Eq. (1) gives the longitudinal and transverse seeing respectively.
In the present case the value of S/d is 0.15 and 0.21 for 52 cm and 38 cm
telescopes respectively.
![\begin{figure}\includegraphics[width=8cm]{ds8858f2.eps}\end{figure}](/articles/aas/full/2000/11/ds8858/Timg29.gif) |
Figure 2:
A comparison of longitudinal and transverse seeing for the two sites
in Devasthal. Straight line has unit slope and zero intercept |
![\begin{figure}\includegraphics[width=18cm]{ds8858f3.eps}\end{figure}](/articles/aas/full/2000/11/ds8858/Timg30.gif) |
Figure 3:
Seeing at Devasthal Site 1 plotted against UT. The date of
observation along with the median seeing value (inside bracket) and the number of points
are indicated sequentially on each panel |


Up: Evaluation of Devasthal site
Copyright The European Southern Observatory (ESO)
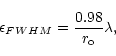
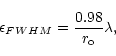
![]() )
of the two
dimensional image position is (cf. Vernin & Muñoz-Tuñón 1995)
given as
)
of the two
dimensional image position is (cf. Vernin & Muñoz-Tuñón 1995)
given as
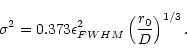
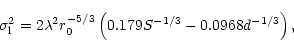
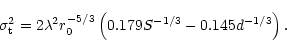
![\begin{figure}\includegraphics[width=8cm]{ds8858f2.eps}\end{figure}](/articles/aas/full/2000/11/ds8858/Timg29.gif)
![\begin{figure}\includegraphics[width=18cm]{ds8858f3.eps}\end{figure}](/articles/aas/full/2000/11/ds8858/Timg30.gif)