6 Testing with astronomical images

It has already been shown by Alard & Lupton (1998) that nearly optimal results ( $\chi^2/{\rm Dof}$ = 1.05) can be achieved within small sub-areas of crowded fields. This of course breaks down as the area is enlarged, since kernel variations are no longer negligible. Comparable results should be achievable but for somewhat larger regions if a variable kernel solution is used.

We test this assumption by extracting 2 larger sub-areas ( $256 \times 256$) from the fields already used in Alard & Lupton (1998), and making image subtraction with constant and variable kernel solutions. The results are shown in Figs. 7 and 8. The constant kernel solution achieved only $\chi^2/{\rm Dof}$ = 1.19, with numerous systematic residuals near the edges of the field. In contrast the subtracted image achieved with a variable kernel ( $\chi^2/{\rm Dof}$ = 1.04) is very close to the $\chi ^2$ obtained with constant kernel solution for a smaller sub-area ( $128 \times 256$). This analysis demonstrates the ability of the new method to deal with kernel variations in crowded-field images. It is certainly useful in this case, since larger areas and thus slightly more robust and reliable results can be obtained in crowded fields. Furthermore the ability to deal with kernel variations is absolutely essential when one has to deal with fields having a low density of bright objects. This is often the case for supernovae searches, Cepheid surveys in other galaxies, and for monitoring of gravitational lenses. Thus the method has many important applications. An example can be found in the analysis of a series of images of the Huchra Lens gravitational lens (Wozniak et al. 1998, 2000).

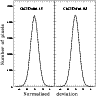Figure 8: Histograms of the normalized deviations in the subtracted images presented in Fig. 7. Left is the histogram for constant kernel solution, and right is the histogram for a fit of kernel variation to order 2. The dashed curve is Gaussian with $\sigma =1$