

Up: Image subtraction using a
Here we briefly summarize the basics of image subtraction (Alard & Lupton 1998).
The essence of the method is to find a convolution kernel (K), that will
transform a reference image (R) to fit a given image I.
In terms of least-squares this is equivalent to solving for a kernel
that will minimize the sum:
 - I(x_i,y_i) \right )^2.
\end{displaymath}](/articles/aas/full/2000/11/ds8706/img6.gif) |
(1) |
Provided the kernel can be decomposed onto basis functions, the above
equations become a simple linear least-squares problem. For the kernel
decomposition we take:
with:
and the generalized index
n = (i,j,k).
The kernel solution can be calculated by solving the following linear system:
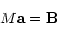 |
(2) |
with:
and:


Up: Image subtraction using a
Copyright The European Southern Observatory (ESO)
 - I(x_i,y_i) \right )^2.
\end{displaymath}](/articles/aas/full/2000/11/ds8706/img6.gif)
 - I(x_i,y_i) \right )^2.
\end{displaymath}](/articles/aas/full/2000/11/ds8706/img6.gif)
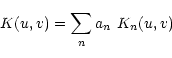
 \ \frac{[R \otimes K_j](x,y)}{\sigma(x,y)^2} \ {\rm d}x{\rm d}y.\end{displaymath}](/articles/aas/full/2000/11/ds8706/img10.gif)
}{\sigma(x,y)^2} \ {\rm d}x{\rm d}y.\end{displaymath}](/articles/aas/full/2000/11/ds8706/img11.gif)