**Table 1:** Image Flags, mainly PDAC information
$\begin{table} \par\begin{displaymath} \tiny \begin{array}{rl} \hline \noalign... ...r\mbox{Note that these flags do not have binary exclusive values.} \end{table}$

During the source extraction process, LDAC produces more flag information (Tables 2 and 3). Artifact flags are not present in the output parameter list because they have been used as a primary selection criteria to filter the catalogue; most of the cosmic rays, glitches and optical ghosts will have been eliminated.

**Table 2:** Extraction Flags (from SExtractor), all LDAC information
$\begin{table} \par\begin{displaymath}\tiny \begin{array}{rl} \hline \noalign{... ...ion}\\ \noalign{\smallskip } \hline \end{array}\end{displaymath} \end{table}$

**Table 3:** Artifact Flags, all LDAC information
$\begin{table} \par\begin{displaymath} \begin{array}{cl} \hline \noalign{\smal... ...nd)}\\ \noalign{\smallskip } \hline \end{array}\end{displaymath} \end{table}$

When dust is present on the mirrors of the telescope and on the lenses of the instrument spurious objects are created. Most are bright and easily recognizable. During the pipeline reduction photometric fluxes are calculated in $7\hbox{$^{\prime\prime}$ }$ and in $15\hbox{$^{\prime\prime}$ }$ apertures. "Dusty-like objects'' give a negative flux in the larger aperture (and its value is set to 99). In their proximity the flat value for the pixels is dominated by their continuous presence in all images along the strip, therefore we end up with an area with negative flux next to the "dusty-like objects''. This area is not always in the same position because of bending of the telescope during the observation of a strip. To eliminate these spurious detections we required that both aperture fluxes were positive. This selection also allowed the removal of glitches not previously flagged, sources too close to the image borders or too close to broad dead pixel regions and dummy sources with photometric errors greater than 0.2 mag.

An additional filtering criterion is based on the diagram of the isophotal area of one object at the $1\sigma$ level of the raw image (Isophotal area-pixels) versus the peak intensity (ln(MaxVal), Peak intensity-ADU); see Fig. 2. Area (3) of point sources (stars) is clearly identified: the objects have a Gaussian intensity energy distribution. Area (2): galaxies are extended objects and, relative to stars, their area increases faster for increasing intensity-ADU. The broadening of the locus of stars is due to the variation of the PSF over the field and of the seeing. Areas (1) and (4) contain cosmic rays and electronic glitches and are easily distinguishable. We accepted only sources in areas (2) and (3); the same cut between stars/galaxies/glitches-cosmic rays was applied to all strips.

Finally we eliminated sources for which the object PSF could not match the instrumental PSF. This led to the loss of a few percent of $K_{\rm s}$ detections; this effect does not depend on the source brightness and arises as a consequence of image defects.

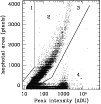$\begin{figure}\resizebox{8.8cm}{!}{\includegraphics{ds1824f2.eps}}\vspace*{4mm} \end{figure}$

Figure 2: Object isophotal area (Area) versus maximum peak intensity (I-peak) for strip 5029 in the J band

Filtering based on the flags, on dust on the detector and on the previous diagram were applied before we made the cross identification between the different wave bands.

4.1 Completeness

A few strips had to be rejected during the reduction phase because of poor quality. These strips have been re-observed, but the data reduction is not yet started and the strips have not been included in the catalogue. Table 4 lists the right ascensions of the absent strips (each covers $1^{\rm m}20^{\rm s}$ in RA). Considering the overlap with adjacent strips we have missed 7.7% and 6.3% of the LMC and SMC regions, respectively.

**Table 4:** Right ascension of the absent strips, each $1^{\rm m}20^{\rm s}$ wide
$\begin{table} \par\begin{displaymath} \begin{array}{lcclc} \hline \noalign{\s... ... s} \\ \noalign{\smallskip } \hline \end{array}\end{displaymath} \end{table}$

Figure 3 displays histograms of the number of sources in the catalogue in 0.05 mag bins. Figures 3a-d refer to the LMC and Figs. 3e-h to the SMC. Table 5 contains the magnitude of the maxima in the various histograms.

A full discussion of these histograms will be given elsewhere (M.R. Cioni, H.J. Habing, M. Messino, in preparation). We limit ourselves to a few comments.

(1) Comparing Figs. 3a and 3b, and similarly Figs. 3e and 3f suggests that (3b) and (3f) contain sources similar to (3a) and (3e), but they are below the detection limit in the $K_{\rm s}$ band. Figures 3b and 3f contain many more sources than Figs. 3a and 3e, respectively.

(2) The I and $K_{\rm s}$ histograms of (3d) and (3h) are approximately scaled down versions of the I and $K_{\rm s}$ histograms in (3a) and (3e). This suggests that they contain the same kind of sources, and that the sources in (3d) and (3h) have not been detected in the I band, i.e. the detection rate in the J band is never 100%, although it will be very close.

(3) The nature of the sources in (3c) and (3g) remain unspecified for the moment.

(4) The magnitudes of the maximum count as given in Table 5 show that the magnitudes referring to the SMC are about 0.25 mag fainter - this reflects the larger distance to the SMC. This conclusion is not true for the counts of sources detected only in I and J. These counts may contain a large foreground component.

$\begin{figure}\resizebox{\hsize}{!}{\includegraphics{ds1824f3.eps}}\vspace*{4mm} \end{figure}$

Figure 3: Differential star counts of sources in 0.05 mag bins for the whole catalogue, with detections in three or two bands. From left to right: LMC and SMC. From top to bottom: sources detected in three wave bands, sources detected only in I and J, sources detected only in J and $K_{\rm s}$ and sources detected only in I and $K_{\rm s}$ . Note that the tip of the RGB is very nicely detected

$\begin{figure}\resizebox{\hsize}{!}{\includegraphics{ds1824f4.eps}}\vspace*{4mm} \end{figure}$

Figure 4: Cumulative star counts of sources in 0.05 mag bins for the whole catalogue, with detections in three or two bands. From left to right: LMC and SMC. From top to bottom: sources detected in three wave bands, sources detected only in I and J, sources detected only in J and $K_{\rm s}$ and sources detected only in I and $K_{\rm s}$

**Table 5:** Magnitude of maximum count (see Fig. 3 and text)
$\begin{table} \par\begin{displaymath}\tiny \begin{array}{lcccclcccc} \hline \... ...m{h}\\ \noalign{\smallskip } \hline \end{array}\end{displaymath} \end{table}$

**Table 6:** Detections
$\begin{table} \par\begin{displaymath} \begin{array}{lrr} \hline \noalign{\sma... ...000 \\ \noalign{\smallskip } \hline \end{array}\end{displaymath} \end{table}$

4.2 Galactic foreground sources

Galactic sources in the foreground have not been removed from the catalogue. Therefore, we now discuss the probability that any given source belongs to the Magellanic Clouds or to the Milky Way Galaxy.

Figure 5a shows that the count of sources detected in all three wave bands has a strong maximum inside the LMC area i.e. $-69\hbox {$^\circ $ }>\delta >-71\hbox {$^\circ $ }$ . Outside of this area the count falls down to a plateau at an average value of 50 sources per 0.5 degrees in declination; this plateau represents the foreground contribution.

In Fig. 5b we show the colour-colour diagram of all sources within the peak area of the LMC, and in Fig. 5c for all sources outside of the LMC. The foreground sources in (5c) are probably ordinary dwarf stars and red giants, for which we expect colours (0.5, 0.5) and (1.0, 1.0), respectively (Bessell & Brett [1988]). The area outside the LMC is about 7 times the area used in Fig. 5b and this explains why the total number of objects within ( $J-K_{\rm s}<1$ ) and (I-J<1) is much larger in Fig. 5c than in Fig. 5b: the fraction of foreground sources in Fig. 5b is very small indeed.

Figures 5d, 5e and 5f refer to sources detected in three wave bands plus sources detected only in I and J. The comparison between Fig. 5d (in the LMC) and Fig. 5e (outside the LMC) shows again what sources may be galactic and what sources are not. Sources in Fig. 5d with I<16 and I-J>1.2 are almost all LMC objects. The same is true for sources with I-J<0.4; these are probably early type main-sequence stars in the LMC. Sources with I>16 and I-J>1 are foreground objects.

Figure 5f shows the histogram obtained by adding up all sources in Fig. 5d (full drawn line) and in Fig. 5e (dashed line) irrespective of the value of I. The difference in distribution of points between Figs. 5d and 5e is obvious. From all strips and all colours we conclude that, on average, 30% of the sources in the catalogue belong to the Galaxy rather than to the Magellanic Clouds. See also Cioni et al. ([1998]) for the separation of foreground and Magellanic stars within DENIS data. A more elaborate discussion will be presented later (M.-R. Cioni and H.J. Habing, in preparation).

$\begin{figure}\resizebox{\hsize}{!}{\includegraphics{ds1824f5.eps}}\vspace*{4mm} \end{figure}$

Figure 5: Sources detected towards the LMC in strip 5068. a), b) and c) refer to sources detected in three wave bands and d), e) and f) also include sources detected only in I and J. In detail: a) histogram of detected sources versus declination in bins of 0.5 degrees, b) colour-colour diagram of sources with $-69\hbox {$^\circ $ }>\delta >-71\hbox {$^\circ $ }$ , c) colour-colour diagram of sources with $\delta >-61$ and $\delta <-77$ , d) colour-magnitude diagram of sources with $-69\hbox {$^\circ $ }>\delta >-71\hbox {$^\circ $ }$ , e) colour-magnitude diagram of sources with $\delta >-61$ and $\delta <-77$ , f) continuous line: differential star counts in bins of 0.05 mag of the same sources in (5d), dashed line: the same for sources in (5e)

$\begin{figure}\resizebox{8.8cm}{!}{\includegraphics{ds1824f6.eps}}\vspace*{4mm} \end{figure}$

Figure 6: Density map towards the LMC per $0.25\times 0.1$ square degrees. Contours are at 1, 10, 25, 50, 75, 100, 150, 200, 300, 400, 500. Ticks on the upper horizontal axis indicate the position of the missing strips. The structure indicate the presence of a bar and spiral arms

$\begin{figure}\resizebox{8.8cm}{!}{\includegraphics{ds1824f7.eps}}\vspace*{3mm} \vspace*{4mm} \end{figure}$

Figure 7: Density map towards the SMC per $0.3\times 0.1$ square degrees. Contours are at 18, 35, 50, 70, 100, 150, 200, 250, 300. Ticks on the upper horizontal axis indicate the position of the missing strips. The concentration of objects on the left side of the SMC structure is due to the galactic globlular cluster 47 Tuc

4.3 Confusion

Figures 6 and 7 contain contour diagrams of source density in bins of constant right ascension. The maximum values is 500 sources in $0.25\times 0.1$ square degrees in the LMC at $\delta = -70.5$ which implies 1 source per 200 arcsec². This is well below the confusion limit.

Note that the confusion is not set by the size of the photometric aperture because the area of the aperture is independent of the detection process. Within the aperture there might be two de-blended sources, each pixel belongs to one or the other source or is shared between the two; the size of the aperture represents the contour limit where this pixel association process has to stop.

4 Data quality

4.1 Completeness

4.2 Galactic foreground sources

4.3 Confusion