In order to facilitate the quantitative studies of voids we have developed an Automated Void Search and Analysis System (AVSAS). Applications of earlier versions of this system are given in Stavrev ([1990a,1990b,1990c,1991,1998]).
AVSAS is a programme package of about 50 modules executing the following functions: (1) preliminary data analysis - homogenization, comparison and combination of data from different sources; (2) local analysis of galaxy and cluster samples - construction and visualization of the nearest-neighbour distance field, search for and parameterization of voids (generation of void catalogues), visualization of the 2-D and 3-D distributions of voids, comparison of void catalogues, identification of the void population and the shell population, construction of void profiles; (3) statistical analysis - statistical comparison of observed samples with random samples, statistical analysis of void catalogues.
The void-search algorithm in AVSAS is based on a definition of the voids as space regions completely devoid of a certain type of objects (clusters, groups, galaxies).
To construct the search algorithm we introduce the concept of a distance field (Stavrev [1990a]). Such an approach has been applied also by Frisch et al. ([1995]), Lindner et al. ([1995]), and recently by Aikio & Mähönen ([1998]).
Let S be a sample of n objects
Ai, i = 1, ..., n,
with Cartesian coordinates
xi, yi, zi in a 3-D coordinate system as described in
Sect. 2.1. We
construct in the spatial volume VS of sample S a cubic grid G,
oriented along the axes ![]() ,
with grid constant
,
with grid constant
![]() Mpc]
and grid nodes gj with coordinates
Mpc]
and grid nodes gj with coordinates
![]() ,
where j = 1, ..., m. For each node the distance to its nearest neighbouring
object is computed from
,
where j = 1, ..., m. For each node the distance to its nearest neighbouring
object is computed from
The local maxima of the d-field indicate regions devoid of objects, while the local minima indicate regions populated by objects. Thus, the task of identification of voids is reduced to the task of determination of the local maxima of a 3-D field.
The local maxima (LM) of the d-field correspond in real space to the centres of the largest empty spheres embedded in the voids. A better approximation of a void (its position, dimension, shape) can be achieved by a system of crossing (overlapping) empty spheres, i.e. by a group of grid nodes defining a local enhancement of the d-field (Stavrev [1991]; see also Stavrev [1990c]). Similar methods for void search have been developed by El-Ad et al. ([1996]) and Aikio & Mähönen ([1998]).The approximation of a void by more than one sphere is shown schematically in Fig. 6.
To determine the LM we introduce first a threshold value
dmin corresponding to the radius of the smallest voids
which are to be identified, i.e. the search for the LM is
restricted over the points of the d-field with
![]() .
The neighbourhood of a point of the d-field with
value di in which a LM is searched is a sphere with radius ri just equal to di. This means that the search procedure uses a
variable neighbourhood which depends on the local properties of the
distribution of objects: the neighbourhood is larger in the more sparsely
populated regions and smaller in the denser regions. This feature of
the procedure makes it suitable for processing spatial
distributions of incomplete samples of objects when the number
density varies strongly depending on the distance or the galactic
latitude.
.
The neighbourhood of a point of the d-field with
value di in which a LM is searched is a sphere with radius ri just equal to di. This means that the search procedure uses a
variable neighbourhood which depends on the local properties of the
distribution of objects: the neighbourhood is larger in the more sparsely
populated regions and smaller in the denser regions. This feature of
the procedure makes it suitable for processing spatial
distributions of incomplete samples of objects when the number
density varies strongly depending on the distance or the galactic
latitude.
AVSAS offers two different methods for determining the LM:
(1) by direct comparison of the d-field values in the
neighbourhood of the d-field points, and (2) by a criterion
![]() for the standard deviation of the d-field values in the
neighbourhood of the d-field points.
for the standard deviation of the d-field values in the
neighbourhood of the d-field points.
Let
![]() be the value of the d-field
in the running node gi0 which has neighbourhood Vi0 with
radius
be the value of the d-field
in the running node gi0 which has neighbourhood Vi0 with
radius
![]() ,
where i = 1, ..., m1,
,
where i = 1, ..., m1,
![]() (m1 is the number of nodes with
(m1 is the number of nodes with
![]() ). Let
Vi0 contain N nodes with values dj, j = 1, ..., N. We define
). Let
Vi0 contain N nodes with values dj, j = 1, ..., N. We define
![]() as a local maximum point
(i.e. a point in the region of a local maximum of the d-field)
in Vi0 if for all j
as a local maximum point
(i.e. a point in the region of a local maximum of the d-field)
in Vi0 if for all j
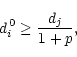
If the parameter p = 0 the above
condition reduces to
![]() for all j.
In this case
for all j.
In this case
![]() is an absolute maximum in Vi0 and corresponds to the
largest empty sphere embedded in the void.
is an absolute maximum in Vi0 and corresponds to the
largest empty sphere embedded in the void.
If p > 0 the algorithm identifies
![]() as a local
maximum point not only when it is an
absolute maximum in Vi0 but also when it is smaller
by less than
as a local
maximum point not only when it is an
absolute maximum in Vi0 but also when it is smaller
by less than
![]() % than the maximum value of the
d-field in Vi0. In this case the algorithm describes
the LM of the d-field by a larger number of points than
for p = 0. Thus,
a void is identified (in the next stages of the procedure)
as a group of LM points, i.e. the void
is approximated by a system of crossing empty spheres.
% than the maximum value of the
d-field in Vi0. In this case the algorithm describes
the LM of the d-field by a larger number of points than
for p = 0. Thus,
a void is identified (in the next stages of the procedure)
as a group of LM points, i.e. the void
is approximated by a system of crossing empty spheres.
We shall call hereafter the empty spheres constituting a void constituent spheres (CS). For convenience, the method for the determination of the LM points by direct comparison using the parameter p will be called p-method.
The second method optionally used in AVSAS for the determination of the LM
points consists of the following. First, we calculate the mean of the
d-field in the neighbourhood Vi0 of the running node
gi0
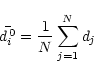
![\begin{displaymath}\sigma_{i}^{0} = \left\{\frac{1}{N-1}\left[\sum_{j=1}^{N} d_{...
...{N} \left(\sum_{j=1}^{N} d_{j}\right)^{2}\right]\right\}^{1/2}.\end{displaymath}](/articles/aas/full/2000/11/ds1766/img64.gif)
Applying any of the two described methods on all
![]() ,
the search procedure produces a set of LM points (or CS). Part of them lie at
the boundaries of the examined space volume. These peripheral LM points can
optionally be removed from further analysis if it is judged that they
are of low significance because of boundary effects or/and sample
incompleteness.
,
the search procedure produces a set of LM points (or CS). Part of them lie at
the boundaries of the examined space volume. These peripheral LM points can
optionally be removed from further analysis if it is judged that they
are of low significance because of boundary effects or/and sample
incompleteness.
In the next stage, the search algorithm groups the LM points on the basis of criteria for their mutual positions. Each defined group of LM points constitutes a separate void in the spatial distribution of the sampled objects. The process of grouping of the LM points is complicated by the percolation of the neighbouring voids, especially when samples of rare tracers of the LSS, such as the rich clusters of galaxies, are used. Often the percolation is strengthened by the sample incompleteness.
Because of the uncertainty in delimiting neighbouring voids the
search algorithm allows for a certain degree of overlap among them.
It offers a choice between three options for grouping the LM points:
(1) compact grouping, (2) medium-compact grouping, and (3) loose
grouping. According to the first option two LM points affiliate to the
same group if the distance between their positions
![]() ,
where k is the
grid constant. This option leads to compact groups of a comparatively
small number of LM points, and consequently a large number of voids
with a high degree
of percolation of neighbouring voids. The criterion for
the medium-compact grouping
is
,
where k is the
grid constant. This option leads to compact groups of a comparatively
small number of LM points, and consequently a large number of voids
with a high degree
of percolation of neighbouring voids. The criterion for
the medium-compact grouping
is
![]() (i.e. a distance equal to the diagonal
of the elementary grid cube). This option produces voids with more
complicated configurations of CS and less overlap with neighbouring
voids than the first option.
The criterion for the third option -
loose grouping -, unlike the first two options, does not depend on k:
two LM points with values d1 and d2 are grouped together if
(i.e. a distance equal to the diagonal
of the elementary grid cube). This option produces voids with more
complicated configurations of CS and less overlap with neighbouring
voids than the first option.
The criterion for the third option -
loose grouping -, unlike the first two options, does not depend on k:
two LM points with values d1 and d2 are grouped together if
![]() .
This criterion assures that the center of
at least one of the two CS lies within the other CS. The voids
produced by loose grouping of LM points may have complicated (irregular)
shapes and a large number of CS, i.e. large sizes. However, the overlap of
neighbouring voids is less (relative to void size) compared with the
first two options.
.
This criterion assures that the center of
at least one of the two CS lies within the other CS. The voids
produced by loose grouping of LM points may have complicated (irregular)
shapes and a large number of CS, i.e. large sizes. However, the overlap of
neighbouring voids is less (relative to void size) compared with the
first two options.
The voids identified with option 1 can be considered as substructures of the voids identified with options 2 and 3, and vice versa - the voids identified with option 3 can be considered as unifications of the voids identified with options 1 and 2.
The choice of the grouping option from 1 to 3 acts parallel to the
choice of a higher value of the parameter p and a lower value
of the
parameter ![]() ,
i.e. towards larger voids with more complicated
shapes.
,
i.e. towards larger voids with more complicated
shapes.
As is seen from the above the void-search algorithm needs choices of
suitable values for the following free parameters:
![]() ,
and the grouping option. The question arises:
given the other values, what values of p and
,
and the grouping option. The question arises:
given the other values, what values of p and ![]() ,
respectively,
are most suitable for the void search?
To answer this question a number of tests of the p-method and
the
,
respectively,
are most suitable for the void search?
To answer this question a number of tests of the p-method and
the ![]() -method have been carried out over two test samples (AR/L and
AR/N, limited to volume V2, see Sect. 2.3) using two values for k (10 and 20
h-1 Mpc), two values for the minimum void diameter
-method have been carried out over two test samples (AR/L and
AR/N, limited to volume V2, see Sect. 2.3) using two values for k (10 and 20
h-1 Mpc), two values for the minimum void diameter
![]() (50 and 80 h-1 Mpc), and two grouping options (medium-compact
and loose grouping). Then, for a certain combination of
(50 and 80 h-1 Mpc), and two grouping options (medium-compact
and loose grouping). Then, for a certain combination of
![]() ,
and the grouping option we check how the
number of identified voids and CS changes as a function of p or
,
and the grouping option we check how the
number of identified voids and CS changes as a function of p or
![]() .
.
The values of
Dmin have been chosen to be roughly equal
to or larger than the mean separation of clusters which is
![]() 53 h-1 Mpc and
53 h-1 Mpc and ![]() 42 h-1 Mpc for the
42 h-1 Mpc for the
![]() and
and ![]() Abell clusters, respectively (Batuski et al. [1991]). With these
Dmin the values of k are chosen to be sufficiently small, so that the LM corresponding
to the smallest identified voids can be determined from statistics
over at least
several dozens of d-field points. The only combination for
which this requirement is not fulfilled is the one with
Dmin = 50 h-1 Mpc, k = 20 h-1 Mpc.
Abell clusters, respectively (Batuski et al. [1991]). With these
Dmin the values of k are chosen to be sufficiently small, so that the LM corresponding
to the smallest identified voids can be determined from statistics
over at least
several dozens of d-field points. The only combination for
which this requirement is not fulfilled is the one with
Dmin = 50 h-1 Mpc, k = 20 h-1 Mpc.
The choice of a sufficiently small value
of k is also of importance for the
accuracy of the determined void parameters. From elementary
considerations follows that
the error of the positions of the CS centres due to
the discreteness of the d-field can be estimated as
![]() .
For the two chosen values of k (20 and
10 h-1 Mpc) the error is 8.66 and 4.33 h-1 Mpc,
respectively. In the latter case the error is comparable to the
diameter of Abell clusters (3 h-1 Mpc), and it is less than
10% of the diameter of the smallest identified voids
(50 h-1 Mpc). Let us also note that the background
contamination, the large peculiar velocities of the cluster members,
and the use of estimated redshifts may lead to positional errors
larger than both chosen values for k.
.
For the two chosen values of k (20 and
10 h-1 Mpc) the error is 8.66 and 4.33 h-1 Mpc,
respectively. In the latter case the error is comparable to the
diameter of Abell clusters (3 h-1 Mpc), and it is less than
10% of the diameter of the smallest identified voids
(50 h-1 Mpc). Let us also note that the background
contamination, the large peculiar velocities of the cluster members,
and the use of estimated redshifts may lead to positional errors
larger than both chosen values for k.
The results from the tests are shown in Fig. 7.
Meaningful values of p and ![]() lie in the ranges
p
lie in the ranges
p
![]() 0.20 and
0.20 and
![]()
![]() 1.0.
Outside these ranges the search procedure
produces a too large number of LM points and this causes difficulties
in delimiting neighbouring voids because of increased overlap among them.
For the case of the medium-compact grouping (Fig. 7, left
panel) the number of voids increases continuously with
increasing p and decreasing
1.0.
Outside these ranges the search procedure
produces a too large number of LM points and this causes difficulties
in delimiting neighbouring voids because of increased overlap among them.
For the case of the medium-compact grouping (Fig. 7, left
panel) the number of voids increases continuously with
increasing p and decreasing ![]() ,
while for the loose
grouping (Fig. 7, right panel) the curves show well
defined maxima in the number of voids. For values of
,
while for the loose
grouping (Fig. 7, right panel) the curves show well
defined maxima in the number of voids. For values of ![]() 0
and
0
and
![]() 2.6-2.7 the search algorithm identifies only
the most significant voids - deep, spherical and well isolated
regions, approximated by single empty spheres.
The increase of p, respectively the decrease of
2.6-2.7 the search algorithm identifies only
the most significant voids - deep, spherical and well isolated
regions, approximated by single empty spheres.
The increase of p, respectively the decrease of ![]() ,
relaxes
the criterion for the selection of LM points, hence the number of voids grows.
At the same time, voids enlarge and start to overlap more due to the
increased number of CS. This causes the merging of neighbouring voids
and consequently a decrease of the number of voids. In the case
of the loose grouping of the LM points, for certain values of the
parameters p and
,
relaxes
the criterion for the selection of LM points, hence the number of voids grows.
At the same time, voids enlarge and start to overlap more due to the
increased number of CS. This causes the merging of neighbouring voids
and consequently a decrease of the number of voids. In the case
of the loose grouping of the LM points, for certain values of the
parameters p and ![]() the process
of merging overtakes the increase of the number of LM points,
hence the number of voids
decreases. If p is left to grow very large or
the process
of merging overtakes the increase of the number of LM points,
hence the number of voids
decreases. If p is left to grow very large or ![]() to become
very small the number of voids tends to 1: a single, continuous,
network structure is formed. For the medium-compact option the
process of merging is not strong enough to stop the growth of the
number of voids with the growth of p, respectively with the decrease of
to become
very small the number of voids tends to 1: a single, continuous,
network structure is formed. For the medium-compact option the
process of merging is not strong enough to stop the growth of the
number of voids with the growth of p, respectively with the decrease of
![]() .
(This is true for the case of compact grouping of the LM points, too.)
.
(This is true for the case of compact grouping of the LM points, too.)
The test curves for the p-method, loose grouping
(Fig. 7b) show maxima approximately for the same
value
pm = 0.10-0.12. The ![]() -method, however,
shows two distinct maxima depending on the value of k:
-method, however,
shows two distinct maxima depending on the value of k:
![]() 1.8 for k = 10 h-1 Mpc and
1.8 for k = 10 h-1 Mpc and
![]() for k = 20 h-1 Mpc.
This stronger dependence of the
for k = 20 h-1 Mpc.
This stronger dependence of the ![]() -method on k in comparison
with the p-method is well outlined in Fig. 7c. On
the other hand, it is seen from Figs. 7a-d that the
-method on k in comparison
with the p-method is well outlined in Fig. 7c. On
the other hand, it is seen from Figs. 7a-d that the
![]() -method is less dependent on
Dmin than the
p-method.
-method is less dependent on
Dmin than the
p-method.
Figure 7b shows that for the p-method the
combination k = 20 h-1 Mpc,
Dmin = 50 h-1 Mpc leads to a substantially higher number of voids
than all other combinations. This case differs from the other
three combinations by its very low ratio
Dmin/k = 2.5. As a result part of the LM points are defined in neighbourhoods
Vi0 containing a very small number of grid points. This probably has
the effect of relaxing the criterion for the selection of voids,
hence increasing the number of voids. The ![]() -method is less
sensitive to this effect. We conclude that values of
Dmin/k lower than 4-5 should be avoided, especially
when the p-method is used.
-method is less
sensitive to this effect. We conclude that values of
Dmin/k lower than 4-5 should be avoided, especially
when the p-method is used.
If we exclude this peculiar case and compare the number of
voids for all other cases at
pm (Fig. 7b)
with the number of voids at
![]() (Fig. 7d) we see that for both methods the number
of voids is in the same range of about 20 - 30
depending slightly on the combination (k,
Dmin), i.e. the agreement between the two methods is good.
(Fig. 7d) we see that for both methods the number
of voids is in the same range of about 20 - 30
depending slightly on the combination (k,
Dmin), i.e. the agreement between the two methods is good.
In order to check how
pm and
![]() depend on
the number density we have used test samples
with growing numbers of objects in the same volume.
These tests show that
pm decreases slightly
with increasing number density, while
depend on
the number density we have used test samples
with growing numbers of objects in the same volume.
These tests show that
pm decreases slightly
with increasing number density, while
![]() is almost
independent of it. The reason for this difference between the two
methods is that the
is almost
independent of it. The reason for this difference between the two
methods is that the ![]() -method is more efficient
than the p-method at rejecting the smaller voids (near
Dmin) in the denser regions as insignificant
fluctuations of the d-field. For the p-method
the increase of the sample density leads to an increase of the number
and the overlap of the CS, hence the number of voids decreases.
This effect is compensated by a smaller
value of
pm which tightens the criterion for
selection of LM points.
-method is more efficient
than the p-method at rejecting the smaller voids (near
Dmin) in the denser regions as insignificant
fluctuations of the d-field. For the p-method
the increase of the sample density leads to an increase of the number
and the overlap of the CS, hence the number of voids decreases.
This effect is compensated by a smaller
value of
pm which tightens the criterion for
selection of LM points.
The tests of the void-search procedure suggest that it can
be optimized by choosing values of
p = pm and
![]() .
That leads to the detection of the maximum
number of voids at a low degree of overlapping of the neighbouring
voids in the case of the loose grouping of the LM points.
These values of p and
.
That leads to the detection of the maximum
number of voids at a low degree of overlapping of the neighbouring
voids in the case of the loose grouping of the LM points.
These values of p and
![]() can be applied as well in the other two options - compact and
medium-compact grouping, in spite of the fact that the number of
detected voids is not maximized, but for the sake of keeping a low
degree of overlapping of the neighbouring voids, hence better
delimited voids.
can be applied as well in the other two options - compact and
medium-compact grouping, in spite of the fact that the number of
detected voids is not maximized, but for the sake of keeping a low
degree of overlapping of the neighbouring voids, hence better
delimited voids.
After voids are identified, AVSAS analyses their properties and defines the following parameters:
(1) Cartesian, equatorial and galactic
coordinates of the CS centres and of the void centre.
The latter is
defined as the centre of the largest CS of the void, and alternatively,
as the centroid of all CS of the void. The centroid is determined as
the centre of gravity of the system of CS. If a void is composed
of
ncs > 1 CS, each one with volume
Vi, i = 1, ...,
ncs, and weight
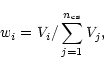
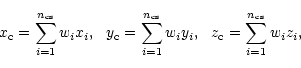
The Cartesian coordinates
![]() in a Lambert equal-area
projection of the CS centres and of the centroid
are computed, too, as described in Sect. 2.1.
in a Lambert equal-area
projection of the CS centres and of the centroid
are computed, too, as described in Sect. 2.1.
(2) Distances are computed to the centres of all CS, as well as to
the CS centroid from the Cartesian coordinates:
![\begin{displaymath}r_i = \sqrt{x_i^2 + y_i^2 + z_i^2}\ \ \ [h^{-1}\,\mathrm{Mpc}],\end{displaymath}](/articles/aas/full/2000/11/ds1766/img87.gif)
(3) Dimensions:
(a) Diameters of the CS are computed directly from the values of the
d-field as
![]() .
.
(b) Void dimensions along ![]() axes are determined from the
projected distances between the centres of those two CS of the void, which are
the farthest apart along each axis, plus their radii. Thus, for the x axis
axes are determined from the
projected distances between the centres of those two CS of the void, which are
the farthest apart along each axis, plus their radii. Thus, for the x axis
(c) The maximum void dimension is determined from the
distance between the centres of the two most widely separated CS of the void
plus the radii of these two CS:
(d) The equivalent void diameter is the diameter of the
sphere whose volume is equal to the total volume
VT of the void (see below):
![\begin{displaymath}D_\mathrm{e} = \left(
\frac{6}{\pi}\,V_\mathrm{T}\right)^{1/3} \ \ [h^{-1}\,\mathrm{Mpc}].\end{displaymath}](/articles/aas/full/2000/11/ds1766/img92.gif)
(4) Sphericity s. This parameter is introduced for a characterization
of the void shape. It is defined as
(5) Volume:
(a) The volume of each CS is computed from
![\begin{displaymath}V_i = \frac{4}{3}\,\pi\,d_{i}^{\,3} \ \ [h^{-3}\,\mathrm{Mpc^3}].\end{displaymath}](/articles/aas/full/2000/11/ds1766/img93.gif)
(b) The total void volume
VT is computed numerically
because of the complicated void shape
(especially when the void is composed of a large number of CS),
by counting
the number of elementary grid cubes
ng in the void
(strictly speaking, the cubes whose centres are inside the void). Then
(6) The objects surrounding the void are defined as the nearest neighbours to the centres of the CS of the void. (See Sect. 6 for a more complete identification of the objects surrounding a void.)
(7) The neighbouring voids of the void are determined from a condition
for overlapping of at least one CS of the void with at least one CS
of the neighbouring void. If d1 and d2 are
the radii of two CS belonging to two different voids, they overlap
if
![]() ,
where
,
where ![]() is the distance between the
centres of the two CS. (Note the difference between this criterion and
the criterion for loose grouping of the LM points in Sect. 3.1.)
is the distance between the
centres of the two CS. (Note the difference between this criterion and
the criterion for loose grouping of the LM points in Sect. 3.1.)
Copyright The European Southern Observatory (ESO)