2 Composition of the observational samples

2.1 Combining redshift data from different sources

The redshift data used in the present study which is limited to the Northern Galactic Hemisphere (NGH) have been compiled from the following sources:

(1) A Compilation of Clusters of Galaxies with Published Redshifts, version 1996.0, by V.S. Lebedev and I.A. Lebedeva (a description of an earlier version is given in Lebedev & Lebedeva [1991]), with redshifts for 1500 clusters and groups (with at least 20 member galaxies) in the NGH, 859 of which are Abell/ACO (A/ACO) clusters.

(2) The NASA/IPAC Extragalactic Database (NED), version 1997 (see description in Madore et al. [1992]), with redshifts for 968 clusters and 190 groups in the NGH, 759 of which are A/ACO clusters.

(3) A Catalogue of Measured Redshifts of Abell Clusters of Galaxies, version 1997 (Andernach & Tago [1998]; Andernach [1997]), with 944 A/ACO clusters in the NGH.

(4) The MX Northern Abell Cluster Redshift Survey (Slinglend et al. [1998]; Batuski et al. [1998]), with redshifts for 62 clusters and 801 galaxies in the NGH.

(5) The Center for Astrophysics (CfA) Redshift Catalogue (ZCAT), version March 3, 1997 (see description in Huchra et al. [1992]), containing redshifts for 21919 galaxies in the NGH.

For convenience, we shall use the following abbreviations for sources 1-5, respectively: LEB, NED, AND, MXS, CfA.

As can be seen, we use four compilations, based on hundreds of original sources, and one new redshift survey, not yet included in any compilation at the time of the present study. They reflect the status of the available redshift data for the clusters, groups, and galaxies in the beginning of 1998.

The numbers of the A/ACO clusters given above include the supplementary southern clusters (ACO S) as well. Let us note that because of the limitation to the NGH (galactic latitude $b \geq$ 0$^{\circ }$) the great majority (> 90%) of the compiled A/ACO clusters are northern Abell clusters (Abell [1958]).

Besides A/ACO clusters the compilations LEB and NED contain also Zwicky clusters (Zwicky et al. [1961]), other types of clusters like poor clusters (Morgan et al. [1975]; Albert et al. [1977]), clusters from the Shane-Wirtanen counts (Shectman [1985]), distant clusters (Gunn et al. [1986]), clusters from the Einstein Observatory Medium Sensitivity Survey (Gioia et al. [1990]) and the ROSAT all-sky survey (Voges [1992]). The groups of galaxies in LEB and NED are mainly nearby groups (Huchra & Geller [1982]), compact groups (Hickson [1982]), groups in the two CfA redshift surveys (Geller & Huchra [1983]; Ramella et al. [1989]), and groups in individual clusters and superclusters (e.g. Ciardullo et al. [1983]; Hopp & Materne [1985]).

No indication which object is a group is given in LEB. We have found from the original data sources referenced in LEB that the number of groups in this compilation (in the NGH) is $\stackrel{\textstyle <}{\sim}$ 100.

The preliminary examination of the spatial distribution of the different tracers from data sources 1-5 shows that only the A/ACO clusters can form complete enough samples in large volumes suitable for large void studies. The completeness limits for all other tracers (non-A/ACO clusters, groups, galaxies) do not go beyond $z\,\sim\,0.03-0.04$. Therefore, we use in this study for void identification only distributions of A/ACO clusters. A limited application of the other tracers has been done only for investigating the substructure of voids in the distribution of rich A/ACO clusters (Sect. 6). (Processing of samples containing galaxies, as well as groups and poor clusters, in smaller and nearer spatial volumes in which the completeness of these objects is higher will be done in a separate study.)

The compilations LEB, NED, and AND are maintained independently by their authors. Furthermore, the compilation versions we use refer to somewhat different times of last update. Therefore, they do not overlap completely and each one of them contains objects which are not present in the other compilations. It follows that by merging them we can increase the total number of objects with spectroscopically measured redshifts.

We have first combined the data from LEB, NED, and MXS. The data from the new unpublished version of AND, only for A/ACO clusters missing in the other three sources, became available to us and was added later as a final enlargement of the data.

After a preliminary check of the data in LEB and NED we have removed from them several dozens of objects which are predominantly subcomponents of clusters with the same coordinates and redshift as the main component, or objects which are erroneously included in the compilations as spectroscopically observed, while, in fact, their redshifts are photometric estimates (Andernach [1997]).

Before combining the data, the redshifts, when heliocentric ( z_h), have been transformed to galactocentric ( z_g) following

$$z_\mathrm{g} = z_\mathrm{h} + \frac{300}{c} \sin l \cos b,$$

where l and b are the galactic coordinates, and c is the speed of light. The distance r to the objects has been derived from the Hubble law assuming a Hubble constant $H_{0} = 100\ \mathrm{km}\ \mathrm{s^{-1}}\ \mathrm{Mpc^{-1}}$. The Cartesian coordinates $x,\ y,\ z$ of the objects have been calculated from their spherical coordinates $r,\ l,\ b$ with the transformation

$$\begin{eqnarray*}x & = & r \cos l \cos b, \\ y & = & r \sin l \cos b, \\ z & = & r \sin b \end{eqnarray*}$$

in a coordinate system centred in the Galaxy with axes x and y directed to l = 0$^{\circ }$, b = 0$^{\circ }$ and l = 90$^{\circ }$, b = 0$^{\circ }$, respectively, and axis z directed to the North Galactic Pole (NGP). In order to be able to construct the 2-D distribution of objects on the sky we have calculated also their rectangular coordinates x_L, y_L in an azimuthal equal-area projection (Lambert projection) from

$$\begin{eqnarray*}A & = & 2\sin \left(45^{\circ } - \frac{b}{2}\right), \\ x_\mathrm{L} & = & A \cos l, \\ y_\mathrm{L} & = & -A \sin l, \end{eqnarray*}$$

where $b \geq 0^{\circ }$, for a coordinate system centred on the NGP and axes x and y directed respectively to l = 0$^{\circ }$, b = 0$^{\circ }$ and l = 270$^{\circ }$, b = 0$^{\circ }$.

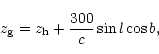
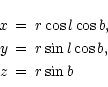
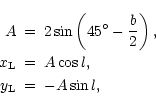
The combination of the data from the different sources is complicated by the presence of discrepant redshifts for a part of the objects, as well as by the necessity to cross-identify correctly (automatically) the identical objects whose designations, coordinates, redshifts, etc. may not exactly coincide in the different sources.

The comparison of the LEB and NED compilations gives 800 coinciding objects whose redshifts are compared in Fig. 1 (for $z \leq$ 0.4). As it is seen, most of the clusters and groups are situated along the line z_LEB = z_NED. However, for several dozens of objects ($\sim$ 10%) the differences $\Delta z$ = z_LEB - z_NED are significant. We have found that in many cases the large $\Delta z$ are an effect of the background contamination which splits clusters into two or more components at different distances along the line-of-sight.

Figure 1: Comparison of the redshifts of clusters and groups in the compilation of Lebedev and Lebedeva ( zLEB) with the redshifts in NED ( zNED) for galactic latitude $b \geq$ 0$^{\circ }$

The MX Survey contains the most reliable data for the cluster redshifts in comparison with the other three sources of data. This is due to the large mean number $\bar{N}_z$ = 9 of cluster members with measured redshifts per cluster, allowing for the elimination of the background contamination. At the same time, only less than half of the clusters in LEB, NED and AND have $N_z \geq 3$.

We can use MXS as a control sample to evaluate the quality of the redshift data in LEB and NED. The comparisons LEB - MXS and NED - MXS for 44 and 42 common objects, respectively, show large redshift discrepancies for about 10% of the compared clusters in both cases. We conclude that (1) the compilations LEB and NED contain similar amounts of large redshift errors, and (2) such errors strongly affect only a comparatively small part of the clusters. Therefore, we accept that both compilations are equally suitable for studies of the large ($\geq$ 50 h^-1 Mpc) voids in the spatial distribution of clusters of galaxies.

The combination of the data from LEB, NED, and MXS has been done by assigning different priorities to them. If an object is present in more than one source it obtains the redshift from that source with the higher priority. We give the highest priority to MXS, and lower, but equal priorities to LEB and NED. Because of this equality we merge the data into two parallel compilations: in the first one the objects which are both in LEB and NED have the redshifts from LEB (compilation CL), and in the second one the redshifts from NED (compilation CN). After adding the data from AND, the two versions of the final compilation contain 1868 objects each, 1014 of which are A/ACO clusters ($\sim$ 45% of all A/ACO clusters in the NGH). The different data sources contribute to compilations CL and CN as follows: MXS - 62 A/ACO clusters both in CL and CN, LEB - 1436 objects (812 A/ACO clusters) in CL and 679 (150) in CN, NED - 267 (37) in CL and 1024 (699) in CN, AND - 103 A/ACO clusters both in CL and CN.

The combination of several sources has led to a 25% increase in comparison with the largest compilation LEB (1500 clusters and groups). For the A/ACO clusters alone, the increase is about 10% compared to AND (944 clusters). Consequently, our compilations offer the possibility of a more complete mapping of the large voids in the spatial distribution of concentrations of galaxies in the NGH.

Besides the two compilations CL and CN we have composed also a compilation of galaxies, hereafter referred to as CG, by merging the data from CfA (ZCAT) and MXS. CG contains 22720 galaxies with $b \geq$ 0$^{\circ }$. It is used in Sect. 6 to examine how galaxies populate the voids in the cluster distribution.

In order to define a volume suitable for void investigations we have first studied the variations of the surface and spatial number densities with decreasing galactic latitude and with increasing redshift, respectively, for the A/ACO clusters from the compilations CL and CN.

The surface number density as a function of galactic latitude for 5$^{\circ }$ bins in b is shown in Fig. 2 for samples from CL separately for all A/ACO clusters (richness class $R \geq$ 0, including the ACO S clusters) and for the $R \geq$ 1 clusters. It is well seen that the effect of galactic obscuration is not strong down to $b = +40^{\circ }$.

Figure 2: Surface number density as a function of galactic latitude for A/ACO clusters of richness classes $R \geq 1$ and $R \geq 0$

Figure 3: Spatial number density as a function of redshift for: a) A/ACO clusters of richness classes $R \geq 1$ and $R \geq 0$, b) $R \geq 1$ A/ACO clusters with measured redshifts, compared with that for the $R \geq 1$ A/ACO clusters with measured or estimated redshifts

The spatial number density as a function of redshift (Fig. 3) is computed for concentric shells of thickness $\Delta z =$ 0.01. Only objects with $b \geq +30^{\circ }$ have been considered in order to reduce the effect of galactic obscuration. Figure 3a shows the variation of the number density with z for the $R \geq 1$ and $R \geq 0$ A/ACO clusters from CL. As can be seen, the spatial density of the $R \geq 1$ clusters remains comparatively high up to $z \approx$ 0.09. In this range the average density is in good agreement with the estimate by Bahcall & Cen (1993) $\bar{n} = 6~10^{-6}~h^{3}~ \mathrm{Mpc}^{-3}$ for the mean spatial density of the $R \geq 1$ A/ACO clusters. In the redshift range 0.09-0.14 the density of the $R \geq 1$ clusters with measured redshifts drops by more than 50%, remaining, however, comparatively constant in this range. For z > 0.14 the density is below 25% of the mean estimate of Bahcall & Cen.

Figure 3a shows that the spatial distribution of the $R \geq 0$ A/ACO clusters is affected by the observational selection even in the redshift range z < 0.09. This is expected since the R = 0 clusters represent an incomplete class of objects in Abell's catalogue. While the density of the $R \geq 0$ clusters for z = 0.04-0.09 agrees well with the estimate by Bahcall & Cen ([1993]) $\bar{n} = 13.5~10^{-6}~h^{3}~\mathrm{Mpc}^{-3}$ for this class of objects, in the nearest volume for z < 0.04 the density agrees better with the more recent estimate $\bar{n} = 26~10^{-6}~h^{3}~\mathrm{Mpc}^{-3}$ of Einasto et al. ([1997]). For z > 0.09 the relative decrease of the density is stronger than for the $R \geq 1$ clusters.

We conclude from the examination of Figs. 2 and 3a that (1) both the $R \geq 1$ and $R \geq 0$ A/ACO clusters show a weak effect of the galactic obscuration for $b \geq +40^{\circ }$, and (2) the sample of $R \geq 1$ A/ACO clusters seems to be complete up to $z \sim$ 0.09 while the sample of $R \geq 0$ clusters is incomplete even in this closer range.

2.2 Clusters with estimated redshifts

One possibility to compensate for the growing incompleteness with distance of the clusters is the usage of estimated distances to the clusters with unmeasured redshifts. A disadvantage of this approach are the large errors (20-30%) of the estimated redshifts (Peacock & West [1992]). The unfavourable effect from the large errors may be reduced by keeping small the fraction of clusters with estimated redshifts when combining them with clusters with measured redshifts.

To estimate the distances to the A/ACO clusters we use the calibration equation (Kalinkov et al. [1985])

$$\begin{eqnarray*}\log z & = & -4.5372 + 0.2132\,m_{10}, \\ [-2mm] & &\ \ \ \,\,\,\!\pm 829 \ \ \ \ \,\,\,\,\pm\! 50 \end{eqnarray*}$$

obtained for a sample of 529 Abell clusters with measured redshifts, where m₁₀ is the magnitude of the 10th brightest cluster member from Abell ([1958]).

We have applied this calibration for 1223 A/ACO clusters in the NGH ( $b \geq 0^{\circ }$) for which no measured redshifts are available. The clusters with photometrically estimated redshifts have been mixed with the clusters with measured redshifts from compilations CL and CN. It is seen from Fig. 3b, where the spatial number density of the $R \geq 1$ A/ACO clusters with measured or estimated redshifts is compared with that of the same type of clusters with measured redshifts (from CL), that after the addition of the clusters with estimated z a deep minimum in the number density distribution is formed at z = 0.10-0.11, followed by a strong enhancement for z = 0.12-0.14. The latter feature is probably due to systematic effects in Abell's catalogue (Abell [1958]). A similar density enhancement in the distance range 300-450 h^-1 Mpc has been found by Scaramella et al. ([1991]) for a sample of Abell clusters, about 45% of which had estimated redshifts, and has been explained as an effect of a systematic overestimate of m₁₀ for the distant clusters in Abell's catalogue. However, in spite of the large errors of the estimated distances, the reality of the maximum in this range cannot be definitely ruled out. It is interesting that the density enhancement in the range 0.12-0.14 coincides well with the third of the peaks in the number of galaxies towards the NGP discovered in the one-dimensional deep survey of Broadhurst et al. ([1990]).

If the density distribution is cut at z = 0.14 the corresponding selection function for the $R \geq 1$ A/ACO clusters with measured or estimated redshifts becomes flat at a density level of 6 10^-6 h³  Mpc^-3, in good agreement with the Bahcall & Cen estimate. Therefore, we conclude that this redshift limit is appropriate for the samples containing clusters with measured or estimated redshifts.

Let us note that if the deep minimum at z = 0.10-0.11 in Fig. 3b is real then the sample of $R \geq 1$ A/ACO clusters with measured redshifts may be complete to $z \approx$ 0.12, i.e. nearly 100 h^-1 Mpc more than the adopted completeness limit z = 0.09.

2.3 The cluster samples

Taking into account the analysis of the completeness of the compilations CL and CN, we define a volume V2 in the NGH with $b \geq +30^{\circ }$ and $z \leq$ 0.14 in which the $R \geq 1$ A/ACO clusters with measured or estimated redshifts form a complete sample and delimit in it a subvolume V1 with $b \geq +40^{\circ }$ and $z \leq$ 0.09 in which the sample of $R \geq 1$ A/ACO clusters with measured redshifts is complete. To reduce the boundary effects we introduce additionally an enlargement of volume V2 down to $b = +20^{\circ }$ and up to z = 0.16. While the void search is limited to volume V2 (i.e. void centres must lie in V2), the objects outside of volume V2 are used only to constrain the voids which intersect the volume boundaries.

Figure 4: Surface distributions in galactic coordinates for samples of A/ACO clusters with $b \geq +20^{\circ }$ and $z \leq$ 0.16 (see Table 1) in Lambert equal-area projection centred on the NGP: a) $R \geq 1$ clusters with measured redshifts, b) $R \geq 1$ clusters with measured or estimated redshifts, c and d) same as a and b) but for the $R \geq 0$ clusters

  

Table 1: Cluster samples for $b \geq +20^{\circ }$ and $z \leq$ 0.16

The samples used in the present study to search for voids are formed by extracting from the compilations CL and CN all A/ACO clusters with $b \geq +20^{\circ }$ and $z \leq$ 0.16 separately for (1) the $R \geq 1$ clusters, and (2) all ($R \geq 0$) A/ACO clusters, and for each of these two tracer types separately for the clusters (1) with measured redshifts, and (2) with measured or estimated redshifts. Thus, a total of 8 samples are composed. Table 1 contains the adopted sample designations and the number of objects in each sample. Letter "L'' or "N'' in the sample designation means extraction from CL or CN, respectively, and "E'' means that the sample contains clusters with estimated redshifts.

Figure 5: Spatial distributions for samples of A/ACO clusters with $b \geq +20^{\circ }$ and $z \leq$ 0.16 (see Table 1) shown as perspective graphs with the coordinate system centred on the Galaxy, axes x and y directed towards l = 0$^{\circ }$, b = 0$^{\circ }$, and l = 90$^{\circ }$, b = 0$^{\circ }$, respectively, axis z directed towards the NGP, and location of the view point at $b \approx$ +18$^{\circ }$, $l \approx$ 320$^{\circ }$: a) $R \geq 1$ clusters with measured redshifts, b) $R \geq 1$ clusters with measured or estimated redshifts, c and d) same as a and b) but for the $R \geq 0$ clusters

For $z \leq$ 0.14 the fraction of clusters with estimated redshifts is about 1/3 of the total number (33% for the $R \geq 1$ clusters and 36% for the $R \geq 0$ clusters). However, for z > 0.12 the number of clusters with estimated redshifts is already larger than that of the measured clusters (see Fig. 3b). There are almost no clusters with only estimated redshifts in the closeby subvolume V1.

Figures 4a-d and 5a-d show 2-D and 3-D visualizations, respectively, of the samples from Table 1 (only the samples extracted from CL are shown). The 2-D distributions are Lambert equal-area projections, centred on the NGP, while the 3-D visualizations are perspective graphs.

The 2-D distributions (Fig. 4) show that the NGH is covered satisfactorily by the observations with the exception of the sparsely populated region at low galactic latitudes around l = 0$^{\circ }$ affected strongly by the galactic obscuration (Abell [1958]; Bahcall & Soneira [1982b]). The inclusion of clusters with estimated redshifts (Figs. 5b and d) increases the completeness but some stratification in the spatial distribution appears at larger distances, most probably due to the systematic overestimate of m₁₀ in Abell's catalogue.