 |
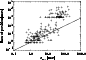
Figure 5: The deviations in position between the Hipparcos Catalogue and the present work as a function of the highest of the formal errors given in Hipparcos for the positional co-ordinates |
We present revised Hipparcos solutions for 257 Hipparcos stars, i.e. different HIP numbers. They are solved as 14 single, 120 double, 28 triple and one quadruple system. A total of 163 systems with 342 components. The results are given in Table 3. For each star we give the HIP number and, when appropriate, a component identifier. This identifier is normally taken from HIP or HIC, but in a few cases we have made an assignment. The solutions published here are based on the NDAC intermediate data. The Hipparcos Catalogue was based on a weighted mean of NDAC and FAST results, which differ on the 1-2 mas level; so differences between our results and those in the Hipparcos Catalogue can be expected to be of this order. The standard errors we give are the formal errors from the least squares solution of the linearized equations and are therefore somewhat optimistic. We also give the number of observations available. For systems with more than one HIP number, this is the total number of observations for the two or three pointings involved. It was nearly always found necessary to exclude a certain number of observations. If this number is low, it speaks in favour of the solution; if on the other hand many observations were rejected, it may mean the solution is uncertain, but it may also have a trivial explanation, like the instrument observing the wrong spot on the sky during the first year or so. Position angle and separation are normally given relative to the A component, but occasionally the B or C component is used. The last column gives various flags. Stars with no solution in the Hipparcos Catalogue (84 components) are flagged "n'' and stars which are not at all in Hipparcos (36 components) are flagged "x''. Of the remaining 222 components which are in Hipparcos, 141 are flagged "l'' to indicate a large deviation from Hipparcos, i.e. more than 0.1 mag or more than 10 mas(/yr) in position, parallax or proper motion. Finally 41 of the systems are flagged "U'', meaning a slightly uncertain solution and the presence of an "R'' indicates a note in Sect. 5.
 |
Figure 5: The deviations in position between the Hipparcos Catalogue and the present work as a function of the highest of the formal errors given in Hipparcos for the positional co-ordinates |
The larger deviations from Hipparcos are listed in Table 1. Only four of the large deviations involve Hipparcos single stars (21000, 58184, 63407, 68822). This reflects partly the fact that double or multiple systems are much more difficult to solve than single stars and partly that the transit data are mainly available for double or suspected double stars. All four stars are suspected doubles, now resolved, and the disagreement we have with Hipparcos for these stars is caused by Hipparcos failing to include the effect of the component and is therefore to be expected despite fairly low formal errors in Hipparcos. Some of the corrections to position, parallax and proper motion presented in Table 1 are very large. For position, errors of many arcseconds, for parallax up to 200 mas and for proper motion hundreds of mas/yr in fact up to 6 arcsec/yr do happen. It may be reassuring, that stars with large errors also have higher than normal standard errors in the Hipparcos Catalogue. Stars with formal position error in HIP below 3.5 mas have at most an error of 37 mas in Table 1. It may be less reassuring that one star with a formal error of 3.9 mas, has in fact an error of 1.3 arcsec. The positional differences for all revisited Hipparcos stars are plotted in Fig. 5 as a function of the highest of the formal errors given in Hipparcos for the positional co-ordinates. We see no Hipparcos stars, with a formal error above 60 mas, which do not have a massive error.
| ID |
|
|
|
ID |
|
|
|
ID |
|
|
|
||||||||
HIP |
mag | mas | mas | mas/yr | HIP | mag | mas | mas | mas/yr | HIP | mag | mas | mas | mas/yr | |||||
7158 |
A | 0.0 | 9 | -6 | 14 | 39827 | B | -0.9 | 1349 | -2 | 204 | 83369 | C | -0.9 | 1304 | 1 | 6 | ||
| 7158 | C | -0.6 | 4909 | -6 | 106 | 40638 | B | -1.5 | 20787 | 4 | 38 | 83371 | B | 0.1 | 8 | 1 | 6 | ||
| 7495 | B | -0.1 | 1279 | 3 | 74 | 43422 | A | 0.6 | 157 | 21 | 82 | 83568 | B | -1.9 | 6280 | 0 | 137 | ||
| 10529 | B | -1.2 | 5612 | -38 | 601 | 43947 | A | 0.5 | 25 | -17 | 7 | 83609 | B | -1.5 | 1378 | 0 | 205 | ||
| 10531 | A | 0.1 | 5 | 12 | 12 | 46860 | B | 2.3 | 5277 | -2 | 46 | 83851 | B | 0.0 | 1455 | -19 | 188 | ||
| 10661 | A | 0.6 | 108 | 5 | 42 | 47107 | B | -0.5 | 1324 | -10 | 82 | 83852 | A | 0.0 | 31 | -19 | 61 | ||
| 11888 | B | 0.1 | 21 | 3 | 8 | 48656 | B | 0.0 | 1463 | 5 | 2 | 84709 | A | 0.4 | 64 | -5 | 24 | ||
| 14559 | B | -0.7 | 3644 | -106 | 176 | 52583 | A | 0.9 | 154 | 8 | 15 | 85153 | B | -0.7 | 1282 | 3 | 6 | ||
| 15689 | B | 0.3 | 1293 | -223 | 310 | 52940 | B | -0.8 | 3663 | -5 | 26 | 85229 | A | 0.0 | 1297 | 5 | 28 | ||
| 17750 | B | -0.9 | 1348 | -7 | 222 | 52942 | A | 0.1 | 16 | -5 | 8 | 85605 | B | -0.5 | 1281 | -198 | 361 | ||
| 17750 | C | -0.7 | 1895 | -7 | 349 | 54133 | B | 0.2 | 2 | -4 | 4 | 86615 | A | 0.7 | 1050 | -9 | 124 | ||
| 18897 | A | 0.1 | 16 | 6 | 13 | 58184 | A | 0.1 | 18 | 1 | 1 | 86961 | B | -2.9 | 3684 | -93 | 55 | ||
| 18899 | B | 0.1 | 6264 | 6 | 213 | 58909 | C | 0.2 | 16 | -3 | 4 | 86963 | A | 0.3 | 107 | -93 | 5 | ||
| 21000 | A | 0.6 | 195 | -76 | 144 | 58910 | B | -0.9 | 1309 | -3 | 4 | 87820 | A | 0.0 | 57 | 7 | 70 | ||
| 21132 | A | 0.0 | 1214 | -19 | 484 | 59272 | A | 0.3 | 7 | 6 | 6 | 90724 | A | 0.0 | 40 | -27 | 37 | ||
| 21132 | B | 0.1 | 1198 | -19 | 484 | 60155 | B | 0.1 | 1370 | -4 | 50 | 90724 | B | 0.0 | 8495 | -27 | 37 | ||
| 22140 | A | 0.1 | 11 | 2 | 15 | 60352 | B | -1.0 | 1566 | 26 | 341 | 93539 | A | 0.4 | 13 | 10 | 31 | ||
| 22140 | B | -0.1 | 285 | 2 | 280 | 62951 | B | -0.4 | 1293 | -46 | 115 | 94223 | B | -0.5 | 1313 | 5 | 590 | ||
| 22140 | C | -0.3 | 1266 | 2 | 26 | 63079 | B | 0.0 | 42 | -1 | 16 | 94223 | C | -0.1 | 1232 | 5 | 8 | ||
| 26220 | B | 0.2 | 44 | -4 | 6 | 63081 | A | 0.0 | 1274 | -1 | 54 | 94227 | A | -0.1 | 24 | 5 | 45 | ||
| 26220 | D | -0.6 | 578 | -4 | 6 | 63407 | A | 0.1 | 16 | -1 | 2 | 95579 | A | 0.0 | 23 | -7 | 24 | ||
| 26221 | A | 0.2 | 14 | -4 | 6 | 63507 | B | 0.0 | 1219 | 14 | 12 | 95579 | B | 0.0 | 9682 | -7 | 24 | ||
| 26224 | C | -0.8 | 1254 | -4 | 6 | 63716 | B | 0.7 | 48 | 2 | 9 | 96493 | B | -1.6 | 20975 | 2 | 237 | ||
| 26237 | A | 0.1 | 11 | -1 | 3 | 63721 | A | 0.0 | 5858 | 2 | 9 | 97096 | B | 0.7 | 1293 | 0 | 3 | ||
| 26948 | B | -2.3 | 23102 | 33 | 68 | 65269 | B | -0.1 | 3704 | -14 | 31 | 97241 | A | 0.2 | 20 | -5 | 10 | ||
| 27070 | B | 0.4 | 1221 | -5 | 2 | 66077 | A | 0.5 | 47 | -8 | 32 | 97241 | B | -1.5 | 6358 | -93 | 431 | ||
| 27600 | B | 0.0 | 15 | -1 | 15 | 67593 | B | -1.6 | 10323 | -53 | 5850 | 98528 | A | 0.2 | 2 | 2 | 3 | ||
| 27604 | C | -0.4 | 1235 | -1 | 68 | 68822 | A | 0.0 | 6 | 5 | 11 | 98534 | C | 0.0 | 8 | 5 | 41 | ||
| 27791 | A | 0.2 | 11 | 1 | 23 | 69799 | B | 0.0 | 2553 | 3 | 59 | 99862 | A | 0.6 | 84 | 5 | 8 | ||
| 28936 | B | -0.1 | 1301 | -1 | 1 | 70940 | B | 0.4 | 3696 | -1 | 92 | 100286 | C | 0.0 | 1289 | 0 | 3 | ||
| 30362 | A | -2.0 | 1100 | -49 | 227 | 70970 | C | 0.0 | 28 | -4 | 60 | 100288 | B | 0.1 | 43 | 0 | 3 | ||
| 30365 | C | 0.5 | 485 | -49 | 227 | 70976 | A | 0.0 | 8 | 3 | 17 | 100289 | A | 0.2 | 6 | -3 | 14 | ||
| 30756 | B | -0.2 | 1263 | -49 | 53 | 71500 | A | -0.2 | 25 | 2 | 16 | 107404 | B | -0.3 | 1269 | 17 | 31 | ||
| 31109 | B | 0.5 | 2596 | 22 | 38 | 71500 | B | 0.4 | 79 | 2 | 4 | 109035 | B | -0.8 | 1279 | 0 | 33 | ||
| 31110 | A | 0.0 | 38 | 22 | 38 | 71502 | C | -1.4 | 4056 | 2 | 895 | 109464 | B | -0.4 | 2631 | -2 | 4 | ||
| 31973 | A | 0.0 | 17 | 0 | 13 | 75805 | A | 0.0 | 2 | -5 | 12 | 110629 | A | 0.0 | 15 | 3 | 4 | ||
| 31973 | B | -1.1 | 18203 | 0 | 13 | 75807 | B | -0.1 | 1473 | -5 | 12 | 110632 | B | -0.5 | 8444 | 3 | 145 | ||
| 32628 | A | 0.3 | 18 | 7 | 13 | 75845 | B | -0.3 | 2766 | 3 | 90 | 114207 | C | -0.1 | 4 | 4 | 15 | ||
| 32738 | B | -0.3 | 2465 | 19 | 38 | 76362 | B | -1.3 | 2549 | -76 | 96 | 114209 | A | 0.1 | 2 | 7 | 13 | ||
| 33383 | A | 0.4 | 29 | -22 | 26 | 76435 | B | -0.5 | 12476 | -6 | 2 | 114791 | A | 0.2 | 40 | 4 | 10 | ||
| 33985 | A | 0.1 | 13 | -9 | 15 | 76563 | A | 0.2 | 6 | -7 | 7 | 114791 | B | 0.0 | 24 | 4 | 10 | ||
| 33985 | B | 0.4 | 38 | -9 | 17 | 76566 | C | 0.1 | 23 | -7 | 7 | 114791 | E | -0.9 | 1330 | 4 | 10 | ||
| 34718 | A | 0.2 | 7 | 4 | 7 | 76566 | D | -0.8 | 1288 | -7 | 7 | 114923 | -0.7 | 1275 | 0 | 49 | |||
| 36113 | A | 0.1 | 14 | 1 | 3 | 77516 | A | 0.2 | 37 | -1 | 2 | 115272 | A | 0.1 | 5 | -1 | 5 | ||
| 38479 | B | 0.0 | 1233 | -1 | 3 | 81562 | B | -0.3 | 2585 | -2 | 66 | 116191 | B | 0.0 | 3648 | 106 | 538 | ||
| 39653 | A | 0.0 | 1210 | 5 | 42 | 82724 | A | 0.1 | 2801 | -102 | 313 | 116191 | C | 0.0 | 3644 | 106 | 538 | ||
| 39653 | B | 0.0 | 17 | 5 | 19 | 82725 | B | -0.2 | 2805 | -195 | 304 | 117226 | C | -0.2 | 1272 | -1 | 18 | ||
Mason et al. ([1999])
resolved nine Hipparcos problem stars, i.e. stars with poor solutions,
with speckle interferometry. They find separations between 0.07 and
0.33 arcsec. Transit data are available for eight of the stars, but
we only managed to solve four. They are HIP 44798, 58184, 63407 and 77516.
Our solutions are consistent with their results.
Of particular interest is the orbiting double HIP 77516, which spans
36![]() of position angle in 6 years.
of position angle in 6 years.
Our sample included, by chance, 22 stars from [Falin & Mignard (1999)] which we decided to keep for comparison. We have solutions for 19 stars and the difference between our solutions and theirs is shown in Table 2. The comparison of the astrometric parameters is for the primary component, while the secondary is compared with respect to position angle and separation. Finally we also give a comparison of the magnitude differences. To give an impression of the internal quality of the solutions, we also give the fraction of rejected observations and representative formal errors. For the benefit of the discussion, the stars are divided in five groups.
For the first four stars, the comparison is hampered by the different
models used. [Falin & Mignard (1999)] always determine one common proper motion and one
common parallax, whereas we in these cases have two different proper
motions and, for the first three, also different parallaxes. For the
first three stars we have differences in proper motion between the
two components of about 200 mas/yr. Taking that into account, there
is no excessive disagreement. The last star, HIP 59154, does show
a rather large disagreement. In this case the separation is
![]() which is close to half the grid period of the Hipparcos instrument.
With a magnitude difference of only 0.05 mag, this will strongly
reduce the modulation of the signal in many scan directions. We
cannot decide which solution is the best, but a comparison of the
rejection rates seems to speak in our favour.
which is close to half the grid period of the Hipparcos instrument.
With a magnitude difference of only 0.05 mag, this will strongly
reduce the modulation of the signal in many scan directions. We
cannot decide which solution is the best, but a comparison of the
rejection rates seems to speak in our favour.
The next three stars illustrate another difficult problem in the
Hipparcos instrument for certain separations. These three doubles have
magnitude differences of 2-3 mag and separations of
17-20 arcsec. These separations are in the steep part of
the
sensitivity curve of the Instantaneous Field of View of the instrument.
Going from
![]() to
to
![]() ,
the sensitivity drops
from 0.8 to 0.2 (cf. Sect. 5.7, Vol. 2 of [ESA 1997]).
To make things worse, the pointing of the instrument may vary one or
two arcsec from observation to observation. This is the reason for
the rather high standard errors and the very large disagreement on
the separations and magnitude differences. For the bright primary
components the agreement is good. We cannot say which solution
is correct, if any, but merely warn that one should not trust
such separations to better than about 100 mas.
,
the sensitivity drops
from 0.8 to 0.2 (cf. Sect. 5.7, Vol. 2 of [ESA 1997]).
To make things worse, the pointing of the instrument may vary one or
two arcsec from observation to observation. This is the reason for
the rather high standard errors and the very large disagreement on
the separations and magnitude differences. For the bright primary
components the agreement is good. We cannot say which solution
is correct, if any, but merely warn that one should not trust
such separations to better than about 100 mas.
The middle group of seven stars is well behaved, separations are not too problematic, rejection rates are small and the deviations are acceptable. The only exception is the disagreement on the magnitude difference for the components of HIP 76435 and HIP 80582.
The next four stars have higher rejection rates and a higher level of disagreement between the two sets of solutions. Still, the disagreements are not more than could be expected when complicated cases are treated in two different ways.
The last star is only included for completeness. According to our analysis our solution is the correct one. The comparison demonstrates the damage to double star parameters when both components have the same grid step error. Both the position angle and the separation are clearly distorted.
This comparison is between two sets of results from basically the same observational material, which has, however, undergone different processes to reach a final form. In the absence of an external comparison, this is the best we can do to validate our results and to point out the weak and the strong points.
| ID |
|
|
|
|
|
|
rej |
|
|
|
|
|
|
||
HIP |
mas | mas/yr | % | % | mas | mas | mas | mas |
|
mas | mag | ||||
1338 |
-11 | 15 | 4 | 41 | 9 | 21 | 2 | 4 | 1 | 13 | 4 | 9.8 | 0 | -100 | .04 |
| 27464 | 10 | -14 | -4 | -9 | 89 | 16 | 0 | 12 | 2 | 23 | 3 | 4.2 | 1 | 16 | -.09 |
| 32628 | 1 | -1 | -3 | -7 | 25 | 24 | 1 | 3 | 2 | 9 | 7 | 8.5 | 1 | -13 | -.13 |
| 59154 | 123 | 295 | -45 | 18 | 101 | 60 | 1 | 11 | 4 | 9 | 5 | .7 | -89 | -378 | -.01 |
| 46949 | 1 | -4 | 3 | 1 | -3 | 2 | 2 | 1 | 1 | 18 | 28 | 19.6 | 0 | -108 | .16 |
| 59193 | 7 | -3 | -1 | -1 | 1 | 0 | 3 | 2 | 3 | 54 | 40 | 17.0 | -1 | 149 | .07 |
| 80198 | -1 | -1 | 0 | -1 | 0 | 0 | 6 | 2 | 1 | 44 | 28 | 18.7 | 0 | 216 | -.28 |
| 21000 | 20 | -14 | 4 | -5 | -6 | 0 | 0 | 7 | 5 | 6 | 6 | 4.4 | 0 | 7 | -.11 |
| 31132 | -17 | 7 | 4 | 10 | -4 | 6 | 3 | 2 | 2 | ||||||
| 33383 | -3 | -1 | -4 | -2 | 3 | 0 | 2 | 6 | 2 | 4 | 4 | 10.0 | 0 | -6 | .02 |
| 38479 | -3 | 4 | -4 | 3 | 0 | 0 | 4 | 2 | 1 | 11 | 11 | 9.4 | 0 | 11 | .08 |
| 76435 | -3 | 4 | -4 | 1 | 2 | 0 | 0 | 2 | 1 | 9 | 7 | 13.5 | 0 | 2 | -.26 |
| 80582 | -3 | 0 | 2 | 2 | -2 | 0 | 4 | 1 | 2 | 18 | 32 | 22.8 | 0 | -50 | .46 |
| 81402 | -5 | 0 | -3 | 8 | 11 | 9 | 1 | 9 | 5 | 8 | 6 | 6.7 | 0 | -2 | .06 |
| 41884 | 0 | 5 | 3 | -12 | -25 | 36 | 2 | 3 | 6 | ||||||
| 51496 | -22 | 1 | 9 | -7 | 16 | 36 | 30 | 3 | 8 | ||||||
| 81694 | -42 | 14 | -58 | 51 | 1 | 35 | 5 | 13 | 11 | 15 | 17 | .6 | 2 | 35 | -.22 |
| 98713 | -1 | 16 | 1 | -2 | -5 | 21 | 2 | 2 | 2 | ||||||
| 34226 | -129 | 1263 | -15 | -26 | -12 | 40 | 3 | 12 | 3 | 15 | 3 | 2.0 | 6 | 339 | -.13 |
Copyright The European Southern Observatory (ESO)