4 CO column densities and excitation

4.1 Column densities

High-latitude clouds such as MBM 32 differ from dark clouds and GMC's by low extinction and low (column) densities, and possibly subthermal excitation of CO. Consequently, ¹²CO transitions might not be optically very thick at all positions in contrast to dark clouds. Thus the standard methods for deriving physical parameters from CO(1-0) data will not be quite correct. However, because the magnitude of the error due to these excitation conditions is not known, we shall derive column densities using the standard LTE method from ¹²CO and ¹³CO(1-0) data, and then discuss these results. Other methods for deriving CO (or H₂) column densities use the integrated ¹²CO(1-0) intensity ( $W_{\rm {CO}}$), by adopting either standard conversion factors, or by calibrating the data by combining CO, H I, and FIR measurements (see e.g. Magnani & Onello [1995], for a discussion of these methods).

To derive LTE column densities from the ¹²CO and ¹³CO(1-0) data, we follow the method outlined by e.g. Brand & Wouterloot ([1998]), and assume for the ¹³CO abundance the value of $2.0\ 10^{-6}$ derived by Dickman ([1978]).

Figure 9: a) Distribution of the IRAS 60 $\mu$m emission associated with MBM 32. The contour levels are 0.4 (0.2) 1.4 MJy sr-1. b) The same for the 100 $\mu$m emission. Contour levels are 2 (1) 9 MJy sr-1. The drawn lines indicate the area observed in 12CO(1-0) with the MRS (Fig. 1a). c) Integrated 12CO(1-0) emission over the velocity range -5 to 7 km s-1. Contour levels are 2 (2) 10 K km s-1. d) Integrated H I emission over the velocity range -30 to +50 km s-1. Contour levels are 150 (10)270 K km s-1

The highest value for the H₂ column density in MBM 32 that we derive is $8.9\ 10^{20}$ cm^-2 at offset (8$^\prime$, 20$^\prime$). The ratio ¹²CO/¹³CO(1-0) increases with $T_{\rm {R}}^*$(¹²CO(1-0)) from 5.2 (>5 K) to 6.9 (2 - 3 K), suggesting a decrease in optical depth from the cloud center to the edge. Due to the smaller ¹³CO line widths the integrated $T_{\rm {R}}^*$ ratio increases from 6.9 to 11.1 in this interval. These ratios are higher than those found in Giant Molecular Clouds, where they are typically 3 - 5. We cannot directly derive column densities towards all positions because ¹³CO(1-0) was not measured at all positions where we have ¹²CO(1-0) HRS data, and therefore we first compared for those positions where this is possible, N(H $_2)_{\rm {LTE}}$ and $W_{\rm {CO}}$ (see Fig. 11). It is seen that the ratio $X^\prime$ = N(H $_2)_{\rm {LTE}}/W_{\rm {CO}}$ is independent of $W_{\rm {CO}}$ (though with a large spread) at a value of 7.0 $\pm$ 2.5 (s.d.) 10¹⁹ cm^-2 (K km s^-1)^-1. To derive cloud masses we use this value, rather than the value of $1.9\ 10^{20}$ cm^-2 (K km s^-1)^-1 (Strong & Mattox [1996]) or $1.6\ 10^{20}$ cm^-2 (K km s^-1)^-1 (Hunter et al. [1997]) found for inner Galaxy clouds. But it is close to the number derived from gamma-ray data by Digel et al. ([1996]) for the Polaris Flare, 0.92 $\pm$ 0.14 10²⁰ cm^-2 (K km s^-1)^-1. Similarly we find from the ¹³CO(1-0) data a ratio N(H $_2)_{\rm {LTE}}/W(^{13}$CO) of 5.4 $\pm$  $0.2\ 10^{20}$ cm^-2 (K km s^-1)^-1. This number will be used to derive masses of clumps embedded in MBM 32.

The resulting masses in the three velocity intervals in Fig. 1a are 16.9 $M_\odot$ (2 - 7 km s^-1), 4.1 $M_\odot$ (-5 - 0 km s^-1), and 0.46 $M_\odot$ (0 - 2 km s^-1), including a factor 1.36 for He, and assuming a distance to the cloud of 100 pc. The cloud-averaged H₂densities for these three regions are then 70, 78, and 135 cm^-3 respectively. It was assumed that the clouds are spherical, which is not very likely, and this may cause the lower mean density for the main cloud component, compared to the other two values. If the depth along the line of sight is smaller, the density for this component is larger than 56 cm^-3. Maximum derived ¹³CO column densities are about $1.5\ 10^{15}$ cm^-2. MBM 32 has a low average extinction of A_B=0.6 mag over an area of $10'\ 30'$ (Heithausen & Mebold [1989]; see also Magnani & de Vries [1986]). The maximum value derived for the extinction (at a resolution of about 8$^\prime$) is only slightly higher. Assuming a peak extinction A_V of 0.8 mag and using N(H) = $2.06\ 10^{21}$ A_V (Bertoldi & McKee [1992]), the ¹³CO abundance would be $1.8\ 10^{-6}$, equal to the Dickman value. However the assumption of a constant ¹³CO abundance in a HLC such as MBM 32 is probably not correct. Van Dishoeck & Black ([1988]) show that near N(H₂) = 10²¹ cm^-2 there is a strong increase of CO abundance with N(H₂). In addition part of the extinction can be related to H I gas rather than to H₂ since the cloud is clearly detected in H I (see Figs. 5-7).

The derived J=1-0 excitation temperatures are between 5 and 9 K, with the highest value of 9.6 K at offset (4$^\prime$, 24$^\prime$). The kinetic temperature of 24 K derived by Schreiber et al. ([1993]) from NH₃observations therefore suggests that CO is subthermally excited. Also the dust temperature of 20 K is higher than $T_{\rm {ex}}$. However also beam filling (the presence of many tiny clumps) could explain lower than expected line temparatures.

4.2 Excitation

To investigate the excitation of CO in MBM 32 we convolved the ¹²CO(1-0) HRS and ¹²CO(2-1) maps to the same angular and velocity resolution. We assumed that there is no emission outside the map area, so that the emission at the edge of the cloud would not be over estimated. From Gaussian fits to all spectra we derived the line ratios of the peak temperatures (1-0)/(2-1) at all positions where both lines were detected. The results are shown in Fig. 12, where we distinguish between the three velocity components in the cloud (2 - 7 km s^-1, -5 - 0 km s^-1, and 0 - 2 km s^-1). For the main component (2 - 7 km s^-1) the line ratios do not significantly vary with position in the cloud, but these ratios are somewhat lower than those of the other two components: the mean values of all positions are 1.93 $\pm$ 0.41 (s.d.; N = 301) (2 - 7 km s^-1), 2.40 $\pm$ 0.81 (N = 60) (-5 - 0 km s^-1), and 2.72 $\pm$ 0.80 (N = 12) (0 - 2 km s^-1).

Figure 10: a,b) Plot of IRAS (ISSA) 100 $\mu$m a) and 60 $\mu$m b) flux density versus integrated H I intensity of the local ( $V_{\rm {lsr}}$ near 0 km$\,$s-1) emission for lines of sight without 12CO(1-0) emission. Crosses indicate positions with $\Delta \alpha <-10$$^\prime$. Filled squares indicate positions with $\Delta \alpha >-10$$^\prime$. The drawn line is the least squares fit through all data points. c,d) Plot of IRAS (ISSA) 100 $\mu$m c) and 60 $\mu$m d) flux density versus integrated 12CO(1-0) intensity. The IRAS emission was corrected for H I emission along each line of sight. The thick line is a least squares fit through all data points. The dashed line was obtained using positions with $\Delta \alpha <-10$$^\prime$ (crosses). The dotted line from positions with -10$^\prime$< $\Delta \alpha < 34$$^\prime$ (filled circles), and the dash-dotted line from positions with $\Delta \alpha >34$$^\prime$ (open circles)

¹²CO(3-2) has been observed in a much smaller region due to the relative weakness of the lines. We compare it in the same way with the ¹²CO(2-1) emission as above. However, because the (3-2) transition has not been observed to the edge of the cloud, we did not add spectra without lines around the observed region before convolving to the lower resolution. This transition was only mapped in two small regions of the main cloud component (2 - 7 km s^-1). The ratio (2-1)/(3-2) of the peak $T_{\rm {R}}^*$ is 2.17 $\pm$ 0.45 (N = 37) in the northern region, and 2.74 $\pm$ 0.51 (N = 22) in the southern region. The difference in the two ratios might be real, but part of it might also be explained by the lower efficiency assumed for part of the measurements in the southern region (those made in 1990/1991). However for observations in this region we found no systematic differences in intensity after efficiency correction between observations made in 1990/1991 and in 1991/1992. The ratio (1-0)/(2-1) in both regions are equal within the uncertainty. As for this ratio (Fig. 14), the ratio (2-1)/(3-2) is not dependent on the $T_{\rm {R}}^*$ (2-1) (see Sect. 4.3).

4.3 A cut through MBM 32 in different transitions

The ratio (2-1)/(3-2) can be studied over a larger range in intensity at some positions where we have observed three transitions to a lower noise level than used for the maps. These are ¹²CO(2-1), ¹³CO(2-1), and ¹²CO(3-2). In these transitions we made a deep cut through part of the cloud at $\Delta \delta =0$$^\prime$. In ¹²CO(2-1) the right ascension range was extended to cover also the negative velocity cloud. The results for both (2-1) transitions are shown in Fig. 13, where the raster size is 1$^\prime$. The upper two panels (Figs. 13a and b) show the ¹²CO(2-1) emission of the negative and positive velocity components at the same scale. For the former one around $\alpha$-offset -17$^\prime$, the shapes of our spectra are consistent with similar deep ¹²CO(1-0) spectra by Magnani et al. ([1990]) in this region: spectra at the west side of this cloud show additional velocity components at the blue side, and those at the east side have red wings. In the higher resolution (30 $^{\prime\prime}$) ¹²CO(2-1) spectra of Magnani et al. ([1990]), these weak components are identified as separate small (<0.03 pc) clumps. In Fig. 13b, also the weak negative velocity emission at positive offsets is visible. Figure 13c shows the ¹³CO(2-1) emission in the same offset range as in Fig. 13b. Part of these data have a higher noise because of a shorter integration time.

The ratio of the ¹²CO(2-1) and ¹³CO(2-1) emission at the positions where the latter line was detected is shown in Fig. 14a. We show both the values determined from the peak intensities and those from the integrated intensity. It is seen that at the positions of strongest ¹³CO emission at offsets of 5$^\prime$ to 8$^\prime$, the ratio is about 11. At offsets west of this range the ration increases only slightly to values between 11 and 13 (with the exception of the position at offset 3$^\prime$). However there is not a systematic increase in this range, as one might expect if the ¹²CO optical depth decreases. This should be confirmed by deeper integrations in the most western part of the cloud. As in the case for the (1-0) ratios, the ratios of the peak $T_{\rm {R}}^*$ are slightly higher (median 11.1) than those of the integrated $T_{\rm {R}}^*$ (median 14.2). Both ratios are higher than those of the (1-0) ratios for the main cloud component (about 6 and 9 for peak and integrated $T_{\rm {R}}^*$, respectively; see Sect. 4.1) and higher than in GMCs (e.g. Kramer et al. [1996] found a ¹³CO/¹²CO(2-1) ratio of 1.5 to 8 for Orion B). We can compare the (2-1) ratios with those for the negative velocity component at offsets in the range -1$^\prime$ to 4$^\prime$. Adding the emission in this range (omitting offset 3$^\prime$) we find ratios of 19.4 $\pm$ 4.3 and 19.0 $\pm$ 10.1 respectively for the peak and integrated intensities of the negative velocity component (the peak ¹³CO(2-1) $T_{\rm {R}}^*$ is 0.028 $\pm$ 0.015 K). For the positive velocity component in this interval these values are 13.4 $\pm$ 0.4 and 13.3 $\pm$ 1.1. If the intrinsic ratio ¹²CO/¹³CO is equal to the typical value in the solar neighbourhood of 76 $\pm$ 7 (Wilson & Rood [1994]), the optical depths in both cloud components are very similar. Because of fractionation, the intrinsic ratio in the outer parts of a HLC such as MBM 32, will decrease slightly (see e.g. Fig. 6 of Turner et al. [1992]), and possibly significantly (van Dishoeck et al. [1991] suggest a factor 2 to 3), while both the ¹²CO and ¹³CO abundance decrease to values much lower than the Dickman ([1978]) one (for ¹³CO). Deriving LTE column densities from the (2-1) data along this line, we find values that are a factor 2-4 lower than those from the (1-0) HRS data at the same positions, while the derived excitation temperatures are almost equal for (1-0) and (2-1). This suggests that the assumptions used for the LTE column densities are not correct, as was found also for other clouds, such as Orion (see e.g. Kramer et al. [1996]). Since for deriving the used abundances similar assumptions were used, it has little influence on the derived cloud masses.

Figure 11: Plot of factor $X^\prime = N$(H $_2)/\int T$dv(12CO(1-0)) versus $\int T$dv(12CO(1-0)). $X^\prime$ was derived from LTE calculations (using J=1-0 data) assuming a 13CO abundance of $2.0\ 10^{-6}$

Figure 12: The ratio of the peak $T_{\rm {R}}^*$ of 12CO(1-0) and (2-1) as a function of 12CO(1-0) intensity for three velocity components in MBM 32. Indicated are average (squares) and median (circles) values for different intervals of $T_{\rm {R}}^*$, together with the standard deviations and mean errors

Figure 13: a) 12CO(2-1) emission distribution along a cut in right ascension at $\Delta \delta =0$$^\prime$ (with respect to $\alpha (1950)=9^{\rm h}28^{\rm m}42^{\rm s}$, $\delta (1950)=+66$$^\circ$5$^\prime$) for the negative velocity component, and b) for the positive velocity component. The range in $V_{\rm {lsr}}$ is -10 to 10 km s-1 for each spectrum. c) The same as b), but for 13CO(2-1)

The distribution of the ¹²CO(3-2) emission on a 40 $^{\prime\prime}$ raster along the same line as in Fig. 13 for (2-1) is show in Fig. 15. The negative velocity emission (Fig. 15a) was observed with lower sensitivity than the positive velocity emission (Fig. 15b). An indication for a minimum near offset +3$^\prime$ in the latter panel is also seen in Fig. 13c. In all transitions the clouds edge appears not very sharp, but the decrease in intensity is steeper than exponential. We compare in Fig. 14b the ¹²CO(2-1) and (3-2) emission after convolution of the latter data to the (2-1) angular resolution. Both cloud components show a line ratio which is independent of position. However the average values for both clouds are different: 2.77 $\pm$ 0.23 for the positive velocity emission at offsets larger than -5$^\prime$, and 2.09 $\pm$ 0.21 for the negative velocity emission. This difference is in the same direction as found for the two mapped regions (see Sect. 4.2). Both regions were again observed in different periods for which different telescope efficiencies were assumed.

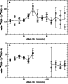Figure 14: a) The line ratios 12CO( 2-1)/13CO(2-1) along the cut through MBM 32 in Fig. 14b. The filled squares indicate the ratios for the peak $T_{\rm {R}}^*$, and the open circles for $\int T_{\rm R}^*$ dv. The dashed line connects the averages of the two values. b) The same for the ratio 12CO( 2-1)/12CO(3-2)

 

 

Table 2: Summary of line ratios and derived X ratios

	$V_{\rm {lsr}}$<0	0< $V_{\rm {lsr}}$<2	$V_{\rm {lsr}}$>2
12CO(1-0)/(2-1)	2.40	2.72	1.93
12CO(2-1)/(3-2)	2.1		2.7
12CO/13CO(1-0) ( $T_{\rm {R}}^*$)			5.2 - 6.9
12CO/13CO(1-0) ( $\int T_{\rm R}^*$dv)			7 - 11
12CO/13CO(2-1)	19.2		13.4
X'(lte) (for 12CO(1-0))	0.7 1020 a
X'(lte) (for 12CO(2-1))	1.4 1020 a
X'(lte) (for 13CO(1-0))	5.4 1020 a
X(fir) (for 12CO(1-0))	>0.2 1020 a
a Units  K km s-1cm-2.

Figure 15: 12CO(3-2) emission distribution along a cut in right ascension at $\Delta \delta =0$$^\prime$ with respect to $\alpha (1950)=9^{\rm h}28^{\rm m}42^{\rm s}$, $\delta (1950)=+66$$^\circ$5$^\prime$ for the negative velocity component a), and for the positive velocity component b). The range in $V_{\rm {lsr}}$ is -10 to 10 km s-1 for each spectrum

In Table 2 we summarize the measured average line ratios in the different parts of the cloud as well as working values for $X^\prime$ for the different transitions which result in column densities equal to the LTE column densities (for ¹²CO(2-1) we assumed a (1-0)/(2-1) ratio of 2 to obtain this $X^\prime$). The ratios can be compared with average $\int T$dv ratios listed by Ingalls et al. ([2000]) for translucent clouds (obtained from data by van Dishoeck et al. ([1991]): ( 1-0)/(2-1)=1.30^+0.59_-0.29, (2-1)/(3-2)=1.82^+0.74_-0.41. Their ¹²CO/¹³CO(1-0) ratio is 7.7 ^+3.4_-1.8. Our ratios appear to be larger, but might be consistent if calibration uncertainties are taken into account.

We have tried to analyze these ratios with an escape probability model (Stutzki & Winnewisser [1985]). It appears that the ¹²CO line ratios are consistent with low density (n<100 cm^-3) gas with $T_{\rm {kin}}$ about 12 K. Also the strongest ¹²CO(1-0) lines of about 6 K can be explained by such gas. However the weaker ¹²CO lines with the same line ratios cannot be explained. It is possible that this is caused by similar gas with a smaller beam filling factor. But then the relatively high ¹²CO/¹³CO(1-0) ratios still cannot be explained. The results of the analysis of the line intensities towards one central position in MBM 32 by Schreiber et al. ([1993]), which indicate a flat density distribution and the constancy of the line ratios within the whole cloud, may suggest that the cloud consist of small clumps (much smaller than the beam size) with average properties that do not change within the mapped area. However the number of such clumps decreases towards the cloud edges. The presence of small clumps within a beam was also suggested by Tauber et al. ([1991]) from high spectral resolution ¹²CO and ¹³CO(1-0) measurements towards Orion. Ingalls et al. ([2000]) conclude from the constant line rations in translucent clouds (including their own ¹²CO(4-3) data) that the clouds consist of high density (n(H ₂)=10^4.5 cm^-3), low temperature (8 K) cells. However we note that they only used the observed line ratios to compare with their LVG models, no line temperatures. We found that in that case solutions are easier to find (see above).

 

 

Table 7: Summary of the results

	$V_{\rm {lsr}}<0$	$0<V_{\rm {lsr}}<2$	$V_{\rm {lsr}}>2$
$T_{\rm {R}}^*(^{12}$CO( $1-0)_{\rm {peak}}$)	2.6 K	1.3 K	4.8 K
$\delta v$ (CO)	1.92 km s-1	2.1 km s-1	1.12 - 1.49 km s-1
$\delta v$ (H I)	4.35 km s-1	4.75 km s-1	4.95 km s-1
$r_{\rm {eq}}$ (CO)	0.57 pc	0.23 pc	0.95 pc
$M_{\rm {gas}}$ (from CO; no He)	3.04 $M_\odot$	0.34 $M_\odot$	12.4 $M_\odot$
$M_{\rm {gas}}$ (from H I; no He)	2.61 $M_\odot$	1.23 $M_\odot$	8.38 $M_\odot$
$M_{\rm {dust}}$	0.020 $M_\odot$		0.053 $M_\odot$

4.4 Cloud structure

We have analysed the CO datacubes with the Gaussclumps algorithm developed by Stutzki & Güsten ([1990]). A detailed discussion of this algorithm and its results for different clouds is given by Kramer et al. ([1998]). The steering parameters were varied in the range found by these authors for their clouds, and those values were taken which resulted in clumps having realistic sizes and linewidths. However the fit-results are not unique - the derived clump parameters depend slightly on the steering parameters. This analysis was done for our ¹²CO(1-0; MRS and HRS), ¹³CO(1-0), and ¹²CO(2-1) cubes. Before analysing it, the ¹³CO(1-0) data cube was filled by interpolation to a fully sampled 2$^\prime$ cube. The results are given in Table 3 for ¹²CO(1-0, MRS), Table 4 for ¹²CO(1-0, HRS), Table 5 for ¹²CO(2-1, MRS) and Table 6 for ¹³CO(1-0, HRS). The limits for linewidths and $T_{\rm {R}}^*$ mentioned in the table header are uncorrected for resolution. Listed are position (offset with respect to $\alpha (1950)=9^{\rm h}28^{\rm m}42^{\rm s}$, $\delta (1950)=+66$$^\circ$5$^\prime$), peak $T_{\rm {R}}^*$, Gaussian half width size, velocity, linewidth, $W_{\rm {CO}}$ mass [using appropriate "X'' factors of $0.7\ 10^{20}$ (¹²CO(1-0)), $1.4\ 10^{20}$ (¹²CO(2-1)), and $5.4\ 10^{20}$ cm^-2 (K km s^-1)^-1 (¹³CO(1-0))], average density, and virial mass. Based on the results of Schreiber et al. ([1993]) we used for the virial masses the assumption of a constant density cloud: $M_{\rm vir}=210$ $\delta v^2r$. Both the average radius r, and the line width $\delta v$ were corrected for the angular and spectral resolution, respectively. The peak $T_{\rm {R}}^*$ was corrected for both effects. We indicated (+ in Col. 10) the clumps that are clearly visible in the original channel maps (without other clumps being subtracted first). These are in general only the strongest ones. We distinguish again the three velocity ranges (see e.g. Fig. 1a), and we only list clumps stronger than the 3$\sigma$ level. They should have line widths significantly above the channel width and be larger than the beam size at least in one direction. Ideally, the clumps listed in Tables 3 to 6 should be the same. We find that the clumps are found in the same general area, but the details differ due to e.g. differences in resolution, and to noise and pointing errors. Comparing the total mass of the clumps found in this way with the total cloud mass in the relevant velocity range it is seen that 40 - 50% of the cloud is in such clumps. The rest of the mass is in smaller clumps (or clumps that are not Gaussian in shape). This fraction is smaller for the weaker cloud components (such as the one in the range 0 - 2 km$\,$s^-1). The largest clumps have a size of 0.5 pc and a mass of about 2 $M_\odot$. Mean H₂ densities in the clumps are several 100 cm^-3 and higher. It is seen that for all clumps the virial mass is much larger than the mass derived using "X''. Whereas it is possible that this means that these clumps are not bound, Turner et al. ([1989]) argue that this difference becomes much less if one takes external pressure on the clumps due to interclump gas into account.

Pound & Blitz ([1993]) list 3 clumps found in a still unpublished ¹³CO(1-0) map of MBM 32. Two of those clumps are located close to clumps listed in Table 6. Our radii are larger because of the angular resolution of the observations.

We have also tried to analyse the cloud data with more detailed algorithms, investigating for instance the power law distribution of clump masses (see e.g. Stutzki et al. [1998]). However the data cubes are not large enough to allow us to obtain reliable results.

Similar to the CO maps, we have investigated the structure of the H I gas. We used a data cube where the broad velocity component had been subtracted. The algorithm finds about 60 clumps larger than the 9 $.\mkern-4mu^\prime$2 resolution. The residual map shows fairly uniform emission with lines of several K. The largest clump found represents the 24 K emission at 3.8 km$\,$s^-1associated with the main part of the molecular cloud. However, most clumps are located at the edge of the mapped region and therefore the data are of no use for a detailed analysis.

Figure 16: a) Correlation of clump size and line width from the analysis of 12CO(1-0) MRS, 12CO(1-0) HRS, 12CO(2-1) MRS, and 13CO(1-0) HRS data. The circles indicate clumps found in the main cloud component, squares are clumps in the small positive velocity component, and triangles are clumps in the negative velocity component. Filled symbols are clumps seen in the original maps (+ in Col. 10 of Tables 3 to 6). b) The same for the correlation between clump size and clump mass. The drawn lines indicate the fits to the filled circles (Eqs. (4) to (7))

In Fig. 16 we compare some of the derived parameters (size, linewidth and mass) of the clumps listed in Tables 3 to 6. We distinguish between the three velocity components and between the clumps which are visible in the original maps before subtracting other Gaussian clumps and those which are not visible in those maps. It is seen in Fig. 16a that the ¹²CO(1-0) linewidths found from the MRS data are somewhat larger than those derived from the HRS data, even after corection for the resolution. There is no significant difference in distribution between the filled and open symbols (+ and -, respectively, in Col. 10 of Tables 3 to 6). We can investigate the linear correlation between the parameters for those velocity components and transitions where the number of clumps found is large enough. We only use the clumps indicated by the filled symbols. These results can be compared with correlations found for integral parameters of HLC. For the main component (¹²CO(1-0) HRS data) we obtained (correlation coefficient 0.86):

$${{\log(\delta v)}} = (0.04 \pm 0.04) + (0.36 \pm 0.05) {\rm {\log(size)}}. \eqno(4)$$

The ¹²CO(2-1) data for the main component gave (correlation coefficient 0.67):

$${{\log(\delta v)}} = (0.38 \pm 0.09) + (0.54 \pm 0.10) {\rm {log(size)}}. \eqno(5)$$

The range in size or the number of data points is too small for the other transitions and components. The average slope of Eqs. (4) and (5), is within the uncertainties equal to the slope found for individual HLC's (0.5 $\pm$ 0.2) or for a sample of known clouds including also GMC's (0.46 $\pm$ 0.03) (see Heithausen [1996]). This could suggest that the density distribution within a clump is the same as the average density distribution within a cloud (if there are no pressure gradients; see Heithausen [1996]).

The data points in Fig. 16b show a larger correlation which is visible in all four panels. We obtain from the same two data sets as above the following results:

$${\rm {log(mass)}} = (0.80 \pm 0.09) + (2.22 \pm 0.11) {\rm {log(size)}} \eqno(6)$$

(¹²CO(1-0) HRS data; correlation coefficient 0.98).

$${\rm {log(mass)}} = (1.10 \pm 0.12) + (2.45 \pm 0.16) {\rm {log(size)}} \eqno(7)$$

(¹²CO(2-1) MRS data; correlation coefficient 0.96).

The mean slope in Eqs. (6) and (7) of about +2.3 is somewhat steeper than the one found for GMC's of 2.0 by Brand & Wouterloot ([1995]) although with a much smaller constant term, which reflects the lower densities of the clumps. The slope is equal to the one found by Heithausen et al. ([1998b]) towards the Polaris Flare from the combination of different data sets.