

Up: Orbital structure and mass
1 Introduction
Table 1:
Setups of the spectroscopic runs. Column 1 gives the run number,
Col. 2 the date, Col. 3 the telescope used, Col. 4 the instrument,
Col. 5 the detector, Col. 6 the wavelength range, Col. 7 the scale in
arcsec/pixel, Col. 8 the slit width in arcsec, Col. 9 the instrumental
resolution in km s-1
| Run |
Date |
Telescope1 |
Instrument2 |
Detector |
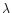 - range
- range |
Scale |
Slit- |

|
| |
|
|
|
|
[Å] |
[''/pix] |
width |
[km s-1] |
| 1 |
31.10-2.11.1992 |
NTT |
EmmiRed |
Tek 1024 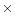 1024 19
1024 19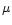
|
4890 - 5430 |
0
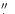 44 44 |
1
|
70 |
| 2 |
4-7.6.1994 |
NTT Remote |
EmmiRed |
Tek 2048  2048 24
2048 24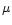
|
4826 - 5474 |
0
 268 268 |
3
|
85 |
| 3 |
26-30.9.1994 |
3.5 CA |
TwinRed |
Tek 1024  1024 24
1024 24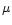
|
4760 - 5640 |
0
 896 896 |
3
 6 6 |
85 |
| 4 |
6-8.6.1994 |
NTT Remote |
EmmiRed |
Tek 2048  2048 24
2048 24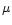
|
4826 - 5474 |
0
 268 268 |
3
|
85 |
| 5 |
26-29.8.1995 |
3.5 CA |
TwinRed |
Tek 1024  1024 24
1024 24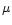
|
4760 - 5640 |
0
 896 896 |
3
 6 6 |
85 |
| 6 |
10-12.3.1996 |
NTT Remote |
EmmiRed |
Tek 2048  2048 24
2048 24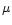
|
4826 - 5474 |
0
 268 268 |
3
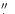
|
85 |
| (1) NTT: ESO 3.5 m New Technology Telescope; 3.5 CA:
3.5 Calar Alto Telescope. |
| (2) EmmiRed: Red Arm of EMMI; TwinRed: Red arm of
the twin spectrograph. |
Much less is known about the mass distributions of elliptical galaxies
than for spirals. Ellipticals are hot stellar systems, and their
circular velocity curves cannot be directly measured, but must be
indirectly inferred from fitting dynamical models to the kinematic
data. Has the luminous matter segregated dissipatively in the halo
potential? Is there a "conspiracy'' between luminous and dark
matter to produce a flat rotation curve, like in spiral galaxies? How
do the mass-to-light ratio, the slope of the circular velocity
curve, or the orbital anisotropy scale with luminosity? The purpose of
this paper is to construct a sample of elliptical galaxies for which
these quantities are well-enough known to address these questions.
Evidence for dark matter in ellipticals comes from X-ray data on their
hot gas atmospheres (e.g., Matsushita et al. [1998];
Loewenstein & White [1999]), from a few cases with cold gas
rings (Bertola et al. [1993]), from gravitational lensing
analyses (Keeton et al. [1998]) and from
stellar-dynamical work. Saglia et al. ([1992])
studied the velocity dispersion profiles of a sample of 10 bright
ellipticals using anisotropic two-component models, finding that the
amount of dark matter inside the half-luminosity radius is of the
order of the luminous mass. Similar results were obtained modeling the
extended profiles of Saglia et al. ([1993]) and Bertin et al. ([1994]), but these authors also showed that some of their
galaxies could be modelled with constant mass-to-light ratio when
more complicated, tangentially anisotropic models were employed.
Van der Marel ([1991]) constructed axisymmetric two-integral
models for a sample of 37 bright ellipticals. He found that these
models predicted too much motion on the major axis and interpreted
this as evidence for anisotropy in the form
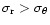 .
From the model fits he also derived mass-to-light ratios and
concluded that these rise approximately as
.
From the model fits he also derived mass-to-light ratios and
concluded that these rise approximately as
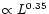 .
These
results were based on velocity dispersion and rotation measurements.
Both modelling approaches described above are subject to some
uncertainty, because of the well-known degeneracy between anisotropy
and mass distribution, given only rotation and velocity dispersion
data.
.
These
results were based on velocity dispersion and rotation measurements.
Both modelling approaches described above are subject to some
uncertainty, because of the well-known degeneracy between anisotropy
and mass distribution, given only rotation and velocity dispersion
data.
In the meantime, both the quality of the available kinematic data and
of the dynamical modelling has improved greatly. Line profile shape
measurements are now available for many ellipticals (e.g.,
Bender et al. [1994]), and in a number of cases these measurements
now extend to sufficiently large radii (
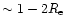 )
that they begin
to constrain the halo mass distribution (e.g., Carollo et al. [1995]).
Theoretical work has shown that such absorption line profile data
contain sufficient information to extract constraints on both
anisotropy and mass distribution (Gerhard [1993]; Merritt [1993]). In
several recent studies, modern data together with sophisticated
modelling methods were used to determine improved mass-to-light
ratios and to estimate M(r) and the anisotropy structure in
individual elliptical galaxies (Rix et al. [1997];
Gerhard et al. [1998];
Emsellem et al. [1999]; Cretton & van den Bosch
[1999];
Saglia et al. [2000]; Matthias & Gerhard [1999];
Gebhardt et al. [2000]).
)
that they begin
to constrain the halo mass distribution (e.g., Carollo et al. [1995]).
Theoretical work has shown that such absorption line profile data
contain sufficient information to extract constraints on both
anisotropy and mass distribution (Gerhard [1993]; Merritt [1993]). In
several recent studies, modern data together with sophisticated
modelling methods were used to determine improved mass-to-light
ratios and to estimate M(r) and the anisotropy structure in
individual elliptical galaxies (Rix et al. [1997];
Gerhard et al. [1998];
Emsellem et al. [1999]; Cretton & van den Bosch
[1999];
Saglia et al. [2000]; Matthias & Gerhard [1999];
Gebhardt et al. [2000]).
The goal of this paper is to extend this work to a sample of
elliptical galaxies. We have selected galaxies that (i) cover as wide
a range in total magnitudes and 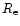 as possible, in order to probe
different regions of the Fundamental Plane, and (ii) are nearly round
(E0-E2), with small rotational velocities, so as to allow us to use
spherical, non-rotating models in analyzing the data. We have obtained
new kinematic data to
as possible, in order to probe
different regions of the Fundamental Plane, and (ii) are nearly round
(E0-E2), with small rotational velocities, so as to allow us to use
spherical, non-rotating models in analyzing the data. We have obtained
new kinematic data to
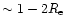 for eight galaxies. In addition, we
have used extended kinematic data for NGC 1399 from Saglia et al.
([2000]), for NGC 2434 from Carollo & Danziger ([1994]), for NGC 3379
from Statler & Smecker-Hane ([1999]), and for NGC 6703 from Gerhard
et al. ([1998]). To these we have added a second sample of ellipticals with
kinematic data to smaller radii, from Bender et al. ([1994], hereafter BSG94),
in order to extend the
total sample to less luminous galaxies and to increase the sample
size. Dynamical models for all of these are shown in this paper.
Based on the results of these models we will be able to investigate
the family properties of ellipticals regarding mass-to-light ratios
and anisotropies; this will be described in a forthcoming paper.
for eight galaxies. In addition, we
have used extended kinematic data for NGC 1399 from Saglia et al.
([2000]), for NGC 2434 from Carollo & Danziger ([1994]), for NGC 3379
from Statler & Smecker-Hane ([1999]), and for NGC 6703 from Gerhard
et al. ([1998]). To these we have added a second sample of ellipticals with
kinematic data to smaller radii, from Bender et al. ([1994], hereafter BSG94),
in order to extend the
total sample to less luminous galaxies and to increase the sample
size. Dynamical models for all of these are shown in this paper.
Based on the results of these models we will be able to investigate
the family properties of ellipticals regarding mass-to-light ratios
and anisotropies; this will be described in a forthcoming paper.
This paper is organised as follows: New spectroscopic observations are
presented in Sect. 2. In Sect. 3
we describe the photometric data used for the modelling, as well as
the distances employed in calculating masses and luminosities. Our
modelling technique, which follows Gerhard et al. ([1998], hereafter
G+98) and Saglia et al. ([2000], hereafter S+2000), is briefly discussed in
Sect. 4. Results are given in Sect. 5,
and in Sect. 6 we present our conclusions.


Up: Orbital structure and mass
Copyright The European Southern Observatory (ESO)