From the EUV observations is well known, that solar atmosphere has significant emission measure in the temperature range, intermediate between coronal-chromospheric values. It should lead to significant contribution to microwave emission, contrary to observations (see Zirin et al. [1991] for review).
As was proposed by Grebinskij ([1987]), this dilemma may be solved,
ifone takes into account the spatial inhomogeneity of atmosphere. Following
that paper, we clarify this conclusion with simple scaling laws for model
example of isothermal plasma volume with some electron temperature
![]() = const, and some fixed value of emission measure
= const, and some fixed value of emission measure
![]() = const. We show, that observed microwave f-f emission
brightness
= const. We show, that observed microwave f-f emission
brightness
![]() of such plasma is strongly dependent on
spatial inhomogeneity and becomes negligible for strong
inhomogeneity.
of such plasma is strongly dependent on
spatial inhomogeneity and becomes negligible for strong
inhomogeneity.
We compare two spatial configurations, in the same projected area,
say
![]() ,
with depth
,
with depth ![]() .
At homogeneous case, with
.
At homogeneous case, with
![]() ,
we have for total emission measure
,
we have for total emission measure
![]() .
As the model inhomogeneity, we assume
en ensemble of some number K of horizontal slabs with dimensions
.
As the model inhomogeneity, we assume
en ensemble of some number K of horizontal slabs with dimensions
![]() and constant number density
and constant number density
![]() inside and zero outside each slab, with the same
inside and zero outside each slab, with the same
![]() ,
and total projected area
,
and total projected area
![]() .
From the EM balance, one would have
.
From the EM balance, one would have
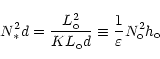 |
(B1) |
| (B2) |
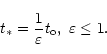 |
(B3) |
| (B4) |
| (B5) |
Equations (B1)-(B5) reveal a scaling nature of brightness depression,
irrespective of detailed spacing of microscale structures: if the filling factor
is sufficiently small (i.e.
![]() ,
and
,
and
![]() ), then at some wave band
), then at some wave band
![]() we
have:
we
have:
![]() .
At the shorter wave band
.
At the shorter wave band
![]() with
with
![]() ,
the emission is optically thin and does not
depend on
inhomogeneity, but remains reduced as
,
the emission is optically thin and does not
depend on
inhomogeneity, but remains reduced as
![]()
![]() .
.
These scalings, together with the observed small EUV-filling factors
![]() ,
solves the problem of consistency results of optical and
microwave observations: at EUV band we have optically thin emission,
proportional to emission measure, but we never detect it at microwaves, with
depressed brightness at the optically-thick regime (with
,
solves the problem of consistency results of optical and
microwave observations: at EUV band we have optically thin emission,
proportional to emission measure, but we never detect it at microwaves, with
depressed brightness at the optically-thick regime (with
![]() ,
but
,
but
![]() >>1 at the cm waveband).
>>1 at the cm waveband).
Copyright The European Southern Observatory (ESO)