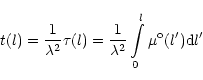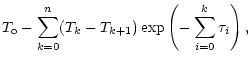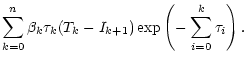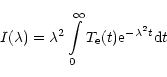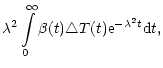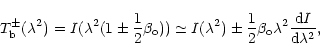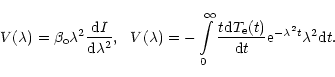Up: Microwave tomography of solar
The radiation transfer equations in the quasi-longitudinal approximation are
decoupled for extraordinary-ordinary (+/-) circular modes with radiation
temperature
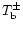 (Zheleznyakov [1970]).
(Zheleznyakov [1970]).
where
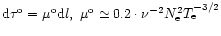 is the bremsstrahlung opacity in an isotropic
plasma,
is the bremsstrahlung opacity in an isotropic
plasma,
 the electron gyrofrequency,
the electron gyrofrequency,
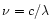 and
and  the angle between the magnetic field
the angle between the magnetic field 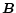 vector and the line of sight. For a plane-layer atmosphere
vector and the line of sight. For a plane-layer atmosphere
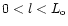 Eq. (A1) can be integrated to obtain the observed brightness temperature
Eq. (A1) can be integrated to obtain the observed brightness temperature
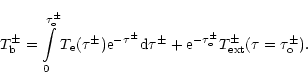 |
(A2) |
where
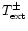 is an incident radiation temperature at the bottom
is an incident radiation temperature at the bottom
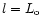 of the atmosphere.
of the atmosphere.
For a single homogeneous layer
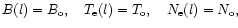
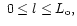 with
an optical depth
with
an optical depth
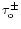 we obtain
we obtain
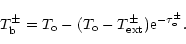 |
(A3) |
We consider the radiation transfer for the Stokes parameters
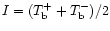 and circular polarization
and circular polarization
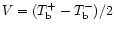 .
After introducing definitions for
.
After introducing definitions for
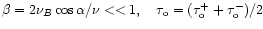 and
and
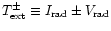 ,
we obtain in a linear
approximation with respect to a small parameter
,
we obtain in a linear
approximation with respect to a small parameter
 the solutions for I and V as
the solutions for I and V as
| I |
= |
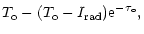 |
|
| V |
= |
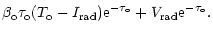 |
(A4) |
We use this solution to construct a solution of the transfer equations in an
inhomogeneous medium by summing up multi-layer solutions. For known
spatial distributions of
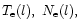 and B(l) we introduce the
frequency-independent radio depth t(l) as a function of the current depth
l, based on an isotropic optical depth
and B(l) we introduce the
frequency-independent radio depth t(l) as a function of the current depth
l, based on an isotropic optical depth 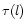
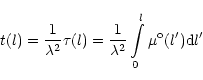 |
(A5) |
and express all spatial distributions as functions of the radio depth t.
We decompose an atmosphere with a total radio depth
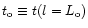 into a sum of n homogeneous layers with solutions given by (A4):
into a sum of n homogeneous layers with solutions given by (A4):
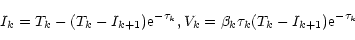 |
(A6) |
where
 the radio depth, Tk the kinetic
temperature for the k-th layer, and
the radio depth, Tk the kinetic
temperature for the k-th layer, and
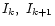 the radiation
temperature at the top and bottom of the k-th layer. For the total
intensity at the top of the atmosphere we have to solve a pair of coupled
equations
for the Stokes parameters I and V
the radiation
temperature at the top and bottom of the k-th layer. For the total
intensity at the top of the atmosphere we have to solve a pair of coupled
equations
for the Stokes parameters I and V
| I |
= |
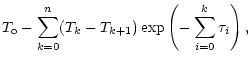 |
|
| V |
= |
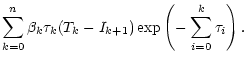 |
(A7) |
To decouple the equations, we should express the
(Tk-Ik+1) in terms of
Tk by means of recurrent use of Eqs. (A6) as
After decoupling the Eqs. (A7) by means of substituting the term
(Tk-Ik+1), in the limit of infinitesimal thin layers we can replace
summation by integration, and in the limit of
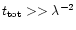 ,
find
the solution of the radiation transfer equation:
,
find
the solution of the radiation transfer equation:
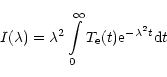 |
(A9) |
In the case of a homogeneous magnetic field distribution
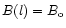 the
radiation transfer Eq. (A1) depends on frequency and magnetic field
only through the combination
the
radiation transfer Eq. (A1) depends on frequency and magnetic field
only through the combination
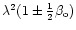 .
Therefore, its solution is ruled by a scaling law
.
Therefore, its solution is ruled by a scaling law
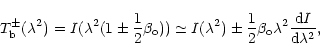 |
(A11) |
and the polarization spectrum is determined by the differential equation
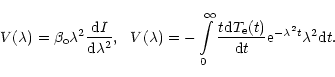 |
(A12) |
These equations have been derived before in a similar form (Bogod &
Gelfreikh [1980]; Grebinskij [1985]) without discussions of
its applicability.


Up: Microwave tomography of solar
Copyright The European Southern Observatory (ESO)
![]() (Zheleznyakov [1970]).
(Zheleznyakov [1970]).
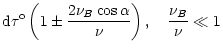
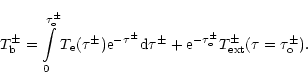
![]()
![]() with
an optical depth
with
an optical depth
![]() we obtain
we obtain