

Up: Oscillator strengths for As
The computed oscillator strengths for various transitions from the
ground state of As I are presented in Tables 2 and 3. There is
not a great deal of experimental and theoretical data available; in
fact, there is data only for the resonance transition
4p3(4S
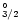 )
)
 4p2(3P)5s(4PJ).
For the J=1/2 component of this transition, the presented calculated
value, 0.0532, lies inside the range of experimental values, 0.059
4p2(3P)5s(4PJ).
For the J=1/2 component of this transition, the presented calculated
value, 0.0532, lies inside the range of experimental values, 0.059
 0.008 ([Bengtsson et al. 1992]), and is in reasonable agreement with
the experimental values 0.074 ([Andersen et al. 1974]) and 0.0734
([Lotrian et al. 1980]).
0.008 ([Bengtsson et al. 1992]), and is in reasonable agreement with
the experimental values 0.074 ([Andersen et al. 1974]) and 0.0734
([Lotrian et al. 1980]).
Calculations have been performed using a variety of
techniques. The present value, 0.0532, is in good agreement with the
theoretical value 0.0584 ([Verner et al. 1994]) and lies between the
theoretical values 0.03 ([Lawrence 1967]) and 0.06
([Holmgren 1975]). For J=3/2, the present value, 0.1064, lies just
inside the experimental range
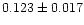 ([Bengtsson et al. 1992]), and
is in reasonable agreement with the experimental values 0.14
([Andersen et al. 1974]) and 0.139 ([Lotrian et al. 1980]). The present value is in
good agreement with the theoretical values 0.11 ([Holmgren 1975]) and
0.113 ([Verner et al. 1994]). For J=5/2, the present value, 0.1596, is in
reasonable agreement with the experimental values 0.21
([Andersen et al. 1974]) and 0.214 ([Lotrian et al. 1980]), and is in excellent
agreement with the theoretical values 0.16 ([Holmgren 1975]) and
0.161 ([Verner et al. 1994]).
([Bengtsson et al. 1992]), and
is in reasonable agreement with the experimental values 0.14
([Andersen et al. 1974]) and 0.139 ([Lotrian et al. 1980]). The present value is in
good agreement with the theoretical values 0.11 ([Holmgren 1975]) and
0.113 ([Verner et al. 1994]). For J=5/2, the present value, 0.1596, is in
reasonable agreement with the experimental values 0.21
([Andersen et al. 1974]) and 0.214 ([Lotrian et al. 1980]), and is in excellent
agreement with the theoretical values 0.16 ([Holmgren 1975]) and
0.161 ([Verner et al. 1994]).
In Table 3 we present our computed oscillator strengths for
transitions to higher s-states and d-states. Due to the absence of any
experimental or theoretical data on these transitions, no comparisons
can be made.
- a
- Andersen & Lindgard (1977): uses the beam-foil technique.
- b
- Migdalek (1976): uses a relativistic semiempirical approach
involving the Dirac equation.
- c
- Migdalek (1983): uses a relativistic Hartree-Fock method.
- d
- Marcinek & Migdalek (1993): uses a multiconfiguration Hartree-Fock method.
- e
- Pinnington et al. (1981): uses the beam-foil technique.
- f
- Aashamar et al. (1983): uses multiconfiguration optimized
potential model.


Up: Oscillator strengths for As
Copyright The European Southern Observatory (ESO)