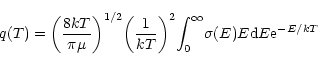3 Results

The collision rates q(T) are taken to be the Maxwellian average of the cross-sections:

$$q(T)={\left(\frac{8kT}{\pi\mu}\right)}^{1/2} {\left(\frac{1}... ...\right)}^{2} {\int_0}^\infty \sigma(E)E{\rm d}E{\rm e}^{-E/kT}$$ (1)

where $\sigma$ is the cross-section and $\mu$ the reduced mass of the system. The present excitation and de-excitation rates are given in Tables 2-5 for 4 temperatures: 300 K, 500 K, 1000 K and 1500 K. Collision rate coefficients for other temperatures are available on request from one of us (Evelyne.Roueff@obspm.fr).

To the best of our knowledge, there is no previous calculation or experiment to which the present results could be compared. It is all the more important to stress the excellent agreement between the new data and those obtained in our previous pure rotational excitation study based on the rigid rotor approximation (Roueff & Zeippen [1999]). This shows that the coupling between rotation and vibration is negligible for the ground state. A typical example is displayed in Fig. 1 for the rotational de-excitation of the first three rotational levels as a function of the relative velocity between HD and He.

 

Table 6: Vibrational quenching rate of the v=1 state in HD due to collisions with He, H and para H₂. Numbers in parentheses are powers of 10

T(K)	He	H	H2
300	1.0(-16)	5.7(-15)	5.8(-17)
500	9.8(-16)	2.6(-14)	3.4(-16)
1000	2.1(-14)	3.4(-13)	8.1(-15)
1500	1.2(-13)	3.5(-12)